Question Number 83411 by ajfour last updated on 02/Mar/20
Commented by ajfour last updated on 02/Mar/20

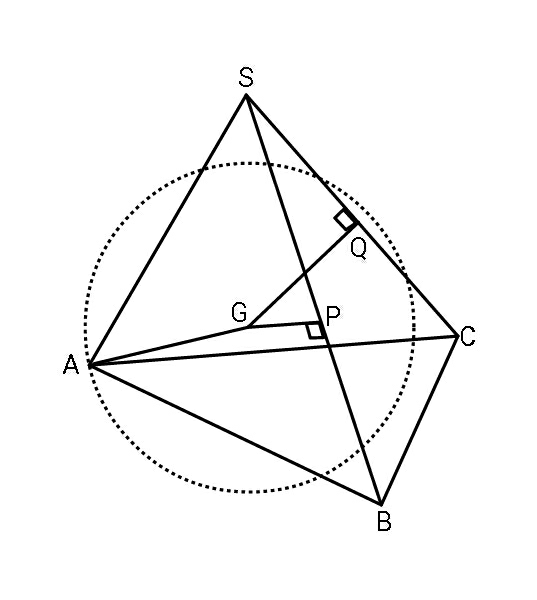
$${Given}\:{a}\:{regular}\:{triangular} \\ $$$${pyramid}\:{with}\:{base}\:{sides}\:\boldsymbol{{a}}\:{and} \\ $$$${lateral}\:{edges}\:\boldsymbol{{a}}\sqrt{\mathrm{2}}.\:{A}\:{sphere} \\ $$$${passes}\:{through}\:{A}\:{and}\:{is}\:{tangent} \\ $$$${to}\:{the}\:{lateral}\:{edges}\:{SB}\:{and}\:{SC} \\ $$$${at}\:{their}\:{midpoints}\:{P}\:{and}\:{Q}. \\ $$$${Find}\:{the}\:{radius}\:{of}\:{the}\:{sphere}. \\ $$
Answered by mr W last updated on 02/Mar/20
Commented by mr W last updated on 02/Mar/20
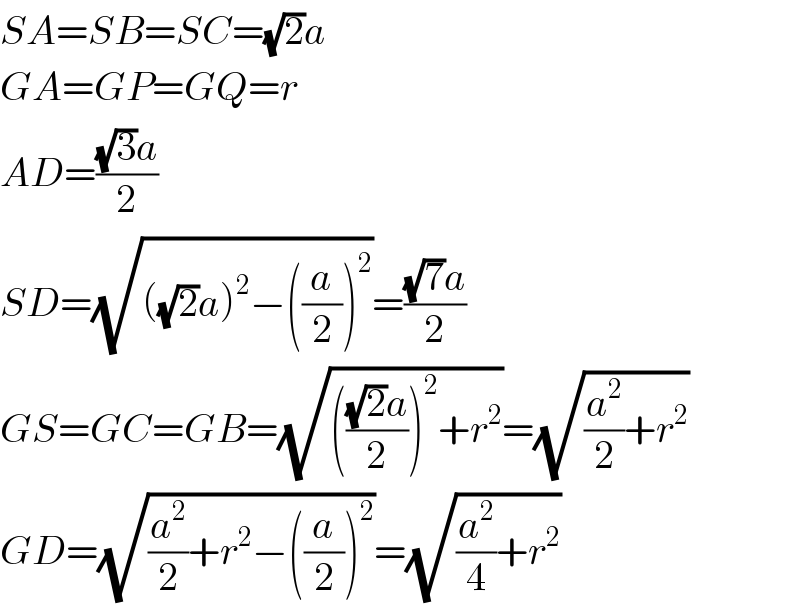
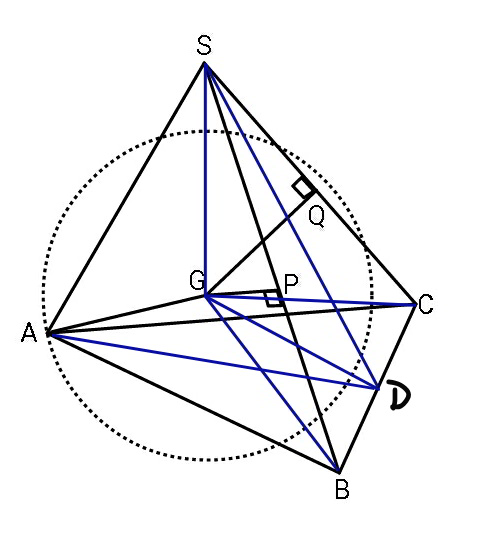
$${SA}={SB}={SC}=\sqrt{\mathrm{2}}{a} \\ $$$${GA}={GP}={GQ}={r} \\ $$$${AD}=\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}} \\ $$$${SD}=\sqrt{\left(\sqrt{\mathrm{2}}{a}\right)^{\mathrm{2}} −\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\sqrt{\mathrm{7}}{a}}{\mathrm{2}} \\ $$$${GS}={GC}={GB}=\sqrt{\left(\frac{\sqrt{\mathrm{2}}{a}}{\mathrm{2}}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} }=\sqrt{\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+{r}^{\mathrm{2}} } \\ $$$${GD}=\sqrt{\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+{r}^{\mathrm{2}} −\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} }=\sqrt{\frac{{a}^{\mathrm{2}} }{\mathrm{4}}+{r}^{\mathrm{2}} } \\ $$
Commented by mr W last updated on 02/Mar/20
Commented by mr W last updated on 02/Mar/20
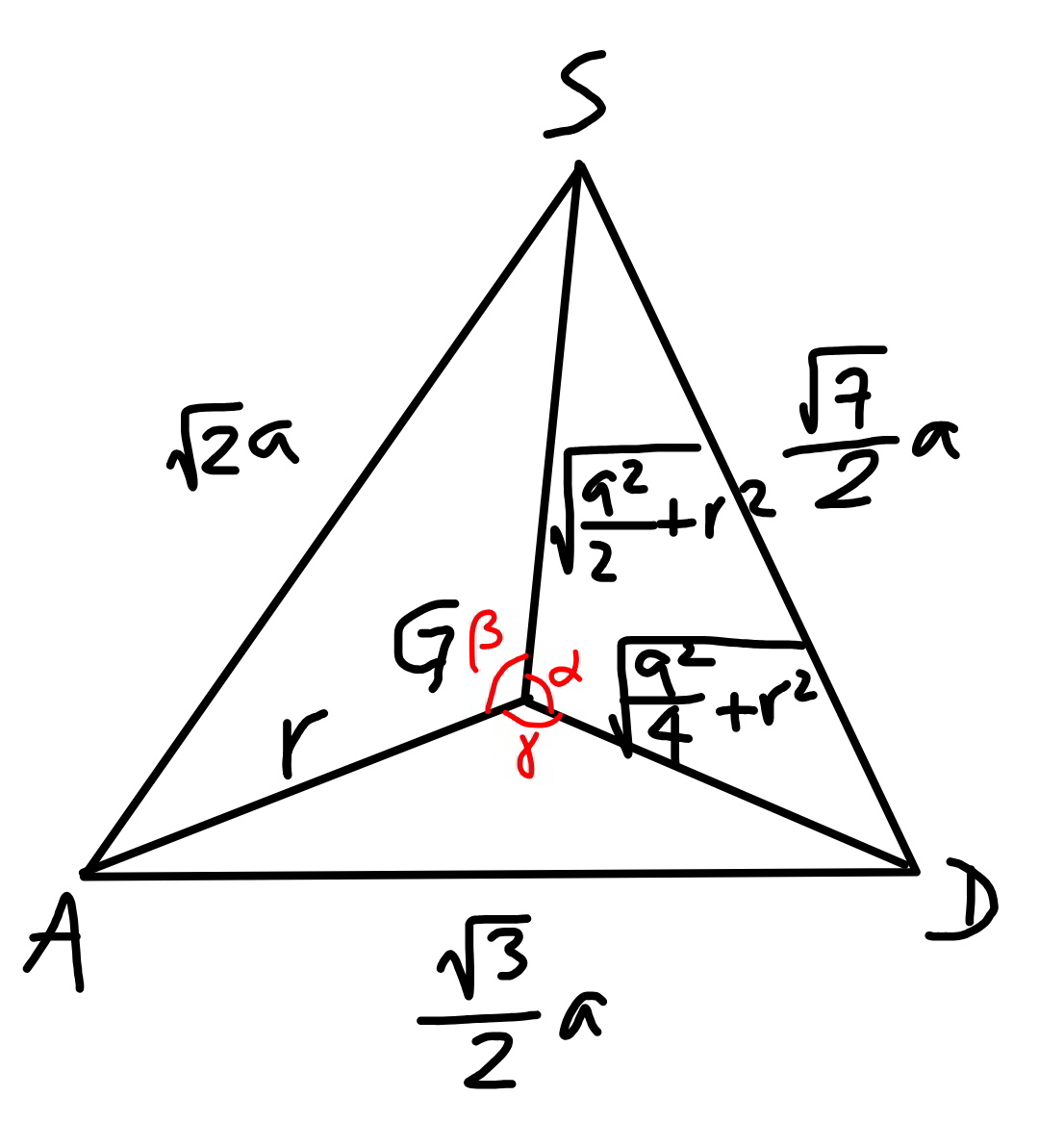
![cos α=(((a^2 /2)+r^2 +(a^2 /4)+r^2 −((7a^2 )/4))/(2(√(((a^2 /2)+r^2 )((a^2 /4)+r^2 )))))=(((2r^2 −a^2 )(√2))/( (√((a^2 +2r^2 )(a^2 +4r^2 ))))) cos β=((r^2 +(a^2 /2)+r^2 −2a^2 )/(2r(√((a^2 /2)+r^2 ))))=(((4r^2 −3a^2 )(√2))/(4r(√(a^2 +2r^2 )))) cos γ=((r^2 +(a^2 /4)+r^2 −((3a^2 )/4))/(2r(√((a^2 /4)+r^2 ))))=((4r^2 −a^2 )/(2r(√(a^2 +4r^2 )))) β+γ=2π−α cos (β+γ)=cos α cos β cos γ−sin β sin γ=cos α (((4r^2 −3a^2 )(√2))/(4r(√(a^2 +2r^2 ))))×((4r^2 −a^2 )/(2r(√(a^2 +4r^2 ))))−((√([16r^2 (a^2 +2r^2 )−2(4r^2 −3a^2 )^2 ][4r^2 (a^2 +4r^2 )−(4r^2 −a^2 )^2 ]))/(4r(√(a^2 +2r^2 ))×2r(√(a^2 +4r^2 ))))=(((2r^2 −a^2 )(√2))/( (√((a^2 +2r^2 )(a^2 +4r^2 ))))) (4r^2 −3a^2 )(4r^2 −a^2 )(√2)−a^2 (√(2(32r^2 −9a^2 )(12r^2 −a^2 )))=8r^2 (2r^2 −a^2 )(√2) 3a^2 −8r^2 =(√((32r^2 −9a^2 )(12r^2 −a^2 ))) 320r^2 =92a^2 ⇒r=((√(115))/(20)) a≈0.536a](https://www.tinkutara.com/question/Q83435.png)
$$\mathrm{cos}\:\alpha=\frac{\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+{r}^{\mathrm{2}} +\frac{{a}^{\mathrm{2}} }{\mathrm{4}}+{r}^{\mathrm{2}} −\frac{\mathrm{7}{a}^{\mathrm{2}} }{\mathrm{4}}}{\mathrm{2}\sqrt{\left(\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+{r}^{\mathrm{2}} \right)\left(\frac{{a}^{\mathrm{2}} }{\mathrm{4}}+{r}^{\mathrm{2}} \right)}}=\frac{\left(\mathrm{2}{r}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\sqrt{\mathrm{2}}}{\:\sqrt{\left({a}^{\mathrm{2}} +\mathrm{2}{r}^{\mathrm{2}} \right)\left({a}^{\mathrm{2}} +\mathrm{4}{r}^{\mathrm{2}} \right)}} \\ $$$$\mathrm{cos}\:\beta=\frac{{r}^{\mathrm{2}} +\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+{r}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} }{\mathrm{2}{r}\sqrt{\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+{r}^{\mathrm{2}} }}=\frac{\left(\mathrm{4}{r}^{\mathrm{2}} −\mathrm{3}{a}^{\mathrm{2}} \right)\sqrt{\mathrm{2}}}{\mathrm{4}{r}\sqrt{{a}^{\mathrm{2}} +\mathrm{2}{r}^{\mathrm{2}} }} \\ $$$$\mathrm{cos}\:\gamma=\frac{{r}^{\mathrm{2}} +\frac{{a}^{\mathrm{2}} }{\mathrm{4}}+{r}^{\mathrm{2}} −\frac{\mathrm{3}{a}^{\mathrm{2}} }{\mathrm{4}}}{\mathrm{2}{r}\sqrt{\frac{{a}^{\mathrm{2}} }{\mathrm{4}}+{r}^{\mathrm{2}} }}=\frac{\mathrm{4}{r}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{r}\sqrt{{a}^{\mathrm{2}} +\mathrm{4}{r}^{\mathrm{2}} }} \\ $$$$\beta+\gamma=\mathrm{2}\pi−\alpha \\ $$$$\mathrm{cos}\:\left(\beta+\gamma\right)=\mathrm{cos}\:\alpha \\ $$$$\mathrm{cos}\:\beta\:\mathrm{cos}\:\gamma−\mathrm{sin}\:\beta\:\mathrm{sin}\:\gamma=\mathrm{cos}\:\alpha \\ $$$$\frac{\left(\mathrm{4}{r}^{\mathrm{2}} −\mathrm{3}{a}^{\mathrm{2}} \right)\sqrt{\mathrm{2}}}{\mathrm{4}{r}\sqrt{{a}^{\mathrm{2}} +\mathrm{2}{r}^{\mathrm{2}} }}×\frac{\mathrm{4}{r}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{r}\sqrt{{a}^{\mathrm{2}} +\mathrm{4}{r}^{\mathrm{2}} }}−\frac{\sqrt{\left[\mathrm{16}{r}^{\mathrm{2}} \left({a}^{\mathrm{2}} +\mathrm{2}{r}^{\mathrm{2}} \right)−\mathrm{2}\left(\mathrm{4}{r}^{\mathrm{2}} −\mathrm{3}{a}^{\mathrm{2}} \right)^{\mathrm{2}} \right]\left[\mathrm{4}{r}^{\mathrm{2}} \left({a}^{\mathrm{2}} +\mathrm{4}{r}^{\mathrm{2}} \right)−\left(\mathrm{4}{r}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{2}} \right]}}{\mathrm{4}{r}\sqrt{{a}^{\mathrm{2}} +\mathrm{2}{r}^{\mathrm{2}} }×\mathrm{2}{r}\sqrt{{a}^{\mathrm{2}} +\mathrm{4}{r}^{\mathrm{2}} }}=\frac{\left(\mathrm{2}{r}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\sqrt{\mathrm{2}}}{\:\sqrt{\left({a}^{\mathrm{2}} +\mathrm{2}{r}^{\mathrm{2}} \right)\left({a}^{\mathrm{2}} +\mathrm{4}{r}^{\mathrm{2}} \right)}} \\ $$$$\left(\mathrm{4}{r}^{\mathrm{2}} −\mathrm{3}{a}^{\mathrm{2}} \right)\left(\mathrm{4}{r}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\sqrt{\mathrm{2}}−{a}^{\mathrm{2}} \sqrt{\mathrm{2}\left(\mathrm{32}{r}^{\mathrm{2}} −\mathrm{9}{a}^{\mathrm{2}} \right)\left(\mathrm{12}{r}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}=\mathrm{8}{r}^{\mathrm{2}} \left(\mathrm{2}{r}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\sqrt{\mathrm{2}} \\ $$$$\mathrm{3}{a}^{\mathrm{2}} −\mathrm{8}{r}^{\mathrm{2}} =\sqrt{\left(\mathrm{32}{r}^{\mathrm{2}} −\mathrm{9}{a}^{\mathrm{2}} \right)\left(\mathrm{12}{r}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)} \\ $$$$\mathrm{320}{r}^{\mathrm{2}} =\mathrm{92}{a}^{\mathrm{2}} \\ $$$$\Rightarrow{r}=\frac{\sqrt{\mathrm{115}}}{\mathrm{20}}\:{a}\approx\mathrm{0}.\mathrm{536}{a} \\ $$
Commented by ajfour last updated on 03/Mar/20

$$\:{i}\:{like}\:{your}\:{solution} \\ $$$$\:{very}\:{much}\:{sir},\:{i}'{ll}\:{try}\:{to}\:{think} \\ $$$${of}\:{some}\:{alternate}\:{way}.. \\ $$
Commented by mr W last updated on 02/Mar/20

$${question}\:{is}\:{nice}.\:{hope}\:{you}\:{have}\:{a}\:{better} \\ $$$${way},\:{using}\:{vector}\:{method}\:{or} \\ $$$${coordinate}\:{method}? \\ $$
Answered by mr W last updated on 03/Mar/20
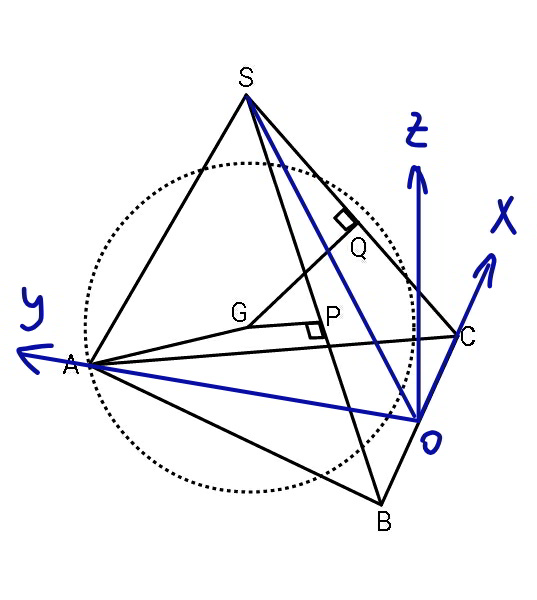
Commented by mr W last updated on 03/Mar/20
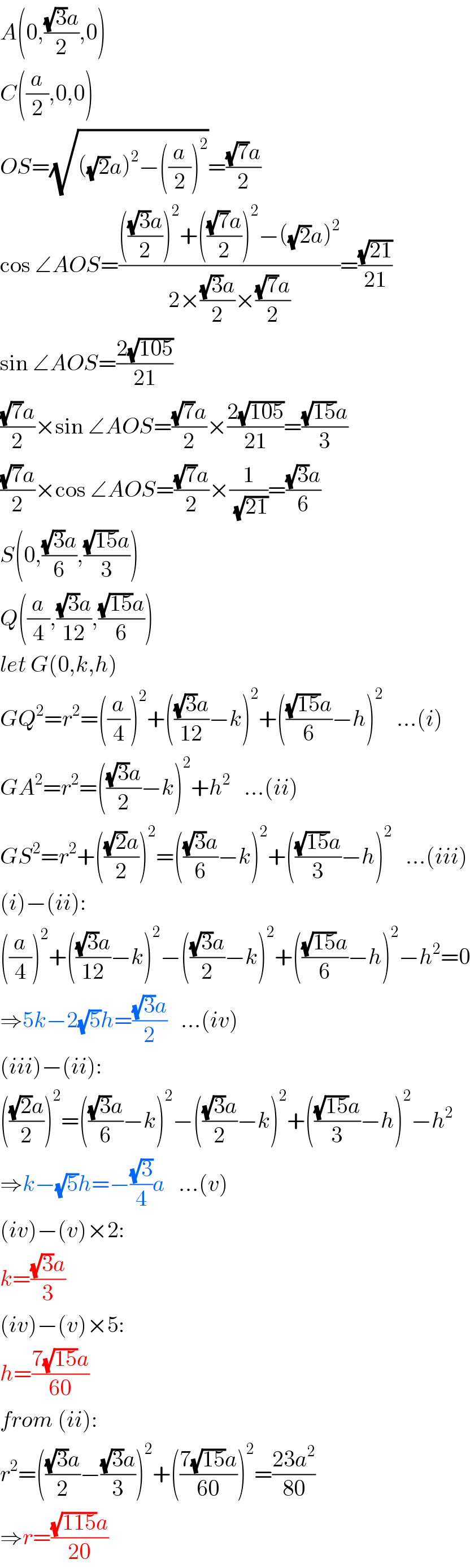
$${A}\left(\mathrm{0},\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}},\mathrm{0}\right) \\ $$$${C}\left(\frac{{a}}{\mathrm{2}},\mathrm{0},\mathrm{0}\right) \\ $$$${OS}=\sqrt{\left(\sqrt{\mathrm{2}}{a}\right)^{\mathrm{2}} −\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\sqrt{\mathrm{7}}{a}}{\mathrm{2}} \\ $$$$\mathrm{cos}\:\angle{AOS}=\frac{\left(\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{7}}{a}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}{a}\right)^{\mathrm{2}} }{\mathrm{2}×\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}}×\frac{\sqrt{\mathrm{7}}{a}}{\mathrm{2}}}=\frac{\sqrt{\mathrm{21}}}{\mathrm{21}} \\ $$$$\mathrm{sin}\:\angle{AOS}=\frac{\mathrm{2}\sqrt{\mathrm{105}}}{\mathrm{21}} \\ $$$$\frac{\sqrt{\mathrm{7}}{a}}{\mathrm{2}}×\mathrm{sin}\:\angle{AOS}=\frac{\sqrt{\mathrm{7}}{a}}{\mathrm{2}}×\frac{\mathrm{2}\sqrt{\mathrm{105}}}{\mathrm{21}}=\frac{\sqrt{\mathrm{15}}{a}}{\mathrm{3}} \\ $$$$\frac{\sqrt{\mathrm{7}}{a}}{\mathrm{2}}×\mathrm{cos}\:\angle{AOS}=\frac{\sqrt{\mathrm{7}}{a}}{\mathrm{2}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{21}}}=\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{6}} \\ $$$${S}\left(\mathrm{0},\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{6}},\frac{\sqrt{\mathrm{15}}{a}}{\mathrm{3}}\right) \\ $$$${Q}\left(\frac{{a}}{\mathrm{4}},\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{12}},\frac{\sqrt{\mathrm{15}}{a}}{\mathrm{6}}\right) \\ $$$${let}\:{G}\left(\mathrm{0},{k},{h}\right) \\ $$$${GQ}^{\mathrm{2}} ={r}^{\mathrm{2}} =\left(\frac{{a}}{\mathrm{4}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{12}}−{k}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{15}}{a}}{\mathrm{6}}−{h}\right)^{\mathrm{2}} \:\:\:…\left({i}\right) \\ $$$${GA}^{\mathrm{2}} ={r}^{\mathrm{2}} =\left(\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}}−{k}\right)^{\mathrm{2}} +{h}^{\mathrm{2}} \:\:\:…\left({ii}\right) \\ $$$${GS}^{\mathrm{2}} ={r}^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{2}}{a}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{6}}−{k}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{15}}{a}}{\mathrm{3}}−{h}\right)^{\mathrm{2}} \:\:\:…\left({iii}\right) \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$$\left(\frac{{a}}{\mathrm{4}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{12}}−{k}\right)^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}}−{k}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{15}}{a}}{\mathrm{6}}−{h}\right)^{\mathrm{2}} −{h}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{5}{k}−\mathrm{2}\sqrt{\mathrm{5}}{h}=\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}}\:\:\:…\left({iv}\right) \\ $$$$\left({iii}\right)−\left({ii}\right): \\ $$$$\left(\frac{\sqrt{\mathrm{2}}{a}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{6}}−{k}\right)^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}}−{k}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{15}}{a}}{\mathrm{3}}−{h}\right)^{\mathrm{2}} −{h}^{\mathrm{2}} \\ $$$$\Rightarrow{k}−\sqrt{\mathrm{5}}{h}=−\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}{a}\:\:\:…\left({v}\right) \\ $$$$\left({iv}\right)−\left({v}\right)×\mathrm{2}: \\ $$$${k}=\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{3}} \\ $$$$\left({iv}\right)−\left({v}\right)×\mathrm{5}: \\ $$$${h}=\frac{\mathrm{7}\sqrt{\mathrm{15}}{a}}{\mathrm{60}} \\ $$$${from}\:\left({ii}\right): \\ $$$${r}^{\mathrm{2}} =\left(\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{3}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{7}\sqrt{\mathrm{15}}{a}}{\mathrm{60}}\right)^{\mathrm{2}} =\frac{\mathrm{23}{a}^{\mathrm{2}} }{\mathrm{80}} \\ $$$$\Rightarrow{r}=\frac{\sqrt{\mathrm{115}}{a}}{\mathrm{20}} \\ $$
