Question Number 83471 by mr W last updated on 02/Mar/20

Commented by mr W last updated on 02/Mar/20

$${The}\:{distances}\:{from}\:{a}\:{point}\:{M}\:{to}\:{the} \\ $$$${vertices}\:{of}\:{a}\:{given}\:{triangle}\:{with} \\ $$$${side}\:{lengthes}\:\boldsymbol{{a}},\:\boldsymbol{{b}},\:\boldsymbol{{c}}\:{are}\:\boldsymbol{{p}},\:\boldsymbol{{q}},\:\boldsymbol{{r}} \\ $$$${respectively}. \\ $$$${Find}\:{the}\:{correlation}\:{between}\:{theses} \\ $$$${distances}. \\ $$
Answered by mr W last updated on 03/Mar/20

$${If}\:{the}\:{point}\:{M}\:{is}\:“{above}''\:{the}\:{triangle} \\ $$$${ABC},\:{then}\:{we}\:{have}\:{a}\:{pyramid}.\:{The} \\ $$$${volume}\:{of}\:{the}\:{pyramid}\:{is}: \\ $$$$\left({see}\:{Q}\mathrm{40469}\right) \\ $$
Commented by mr W last updated on 03/Mar/20

Commented by mr W last updated on 03/Mar/20
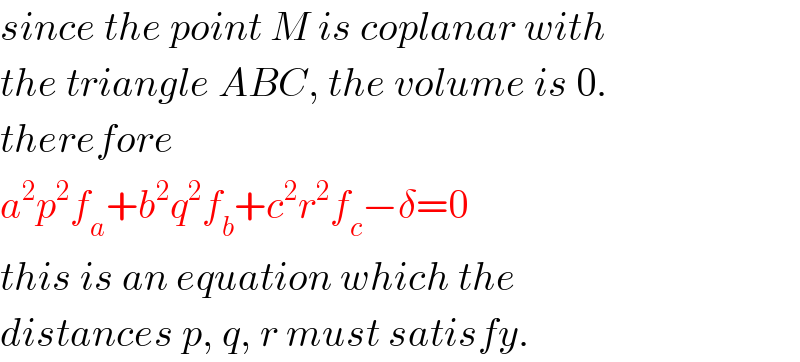
$${since}\:{the}\:{point}\:{M}\:{is}\:{coplanar}\:{with} \\ $$$${the}\:{triangle}\:{ABC},\:{the}\:{volume}\:{is}\:\mathrm{0}. \\ $$$${therefore} \\ $$$${a}^{\mathrm{2}} {p}^{\mathrm{2}} {f}_{{a}} +{b}^{\mathrm{2}} {q}^{\mathrm{2}} {f}_{{b}} +{c}^{\mathrm{2}} {r}^{\mathrm{2}} {f}_{{c}} −\delta=\mathrm{0} \\ $$$${this}\:{is}\:{an}\:{equation}\:{which}\:{the} \\ $$$${distances}\:{p},\:{q},\:{r}\:{must}\:{satisfy}. \\ $$
Answered by mr W last updated on 03/Mar/20
![let α=∠BMC, β=∠CMA, γ=∠AMB cos α=((q^2 +r^2 −a^2 )/(2qr)) cos β=((r^2 +p^2 −b^2 )/(2rp)) cos γ=((p^2 +q^2 −c^2 )/(2pq)) α+β=2π−γ cos (α+β)=cos γ ((q^2 +r^2 −a^2 )/(2qr))×((r^2 +p^2 −b^2 )/(2rp))−((√(4q^2 r^2 −(q^2 +r^2 −a^2 )^2 ))/(2qr))×((√(4r^2 p^2 −(r^2 +p^2 −b^2 )^2 ))/(2rp))=((p^2 +q^2 −c^2 )/(2pq)) ⇒(q^2 +r^2 −a^2 )(r^2 +p^2 −b^2 )−(√([4q^2 r^2 −(q^2 +r^2 −a^2 )^2 ][4r^2 p^2 −(r^2 +p^2 −b^2 )^2 ]))=2r^2 (p^2 +q^2 −c^2 )](https://www.tinkutara.com/question/Q83528.png)
$${let}\:\alpha=\angle{BMC},\:\beta=\angle{CMA},\:\gamma=\angle{AMB} \\ $$$$\mathrm{cos}\:\alpha=\frac{{q}^{\mathrm{2}} +{r}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{qr}} \\ $$$$\mathrm{cos}\:\beta=\frac{{r}^{\mathrm{2}} +{p}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{rp}} \\ $$$$\mathrm{cos}\:\gamma=\frac{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{pq}} \\ $$$$\alpha+\beta=\mathrm{2}\pi−\gamma \\ $$$$\mathrm{cos}\:\left(\alpha+\beta\right)=\mathrm{cos}\:\gamma \\ $$$$\frac{{q}^{\mathrm{2}} +{r}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{qr}}×\frac{{r}^{\mathrm{2}} +{p}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{rp}}−\frac{\sqrt{\mathrm{4}{q}^{\mathrm{2}} {r}^{\mathrm{2}} −\left({q}^{\mathrm{2}} +{r}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{2}} }}{\mathrm{2}{qr}}×\frac{\sqrt{\mathrm{4}{r}^{\mathrm{2}} {p}^{\mathrm{2}} −\left({r}^{\mathrm{2}} +{p}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} }}{\mathrm{2}{rp}}=\frac{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{pq}} \\ $$$$\Rightarrow\left({q}^{\mathrm{2}} +{r}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\left({r}^{\mathrm{2}} +{p}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)−\sqrt{\left[\mathrm{4}{q}^{\mathrm{2}} {r}^{\mathrm{2}} −\left({q}^{\mathrm{2}} +{r}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{2}} \right]\left[\mathrm{4}{r}^{\mathrm{2}} {p}^{\mathrm{2}} −\left({r}^{\mathrm{2}} +{p}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} \right]}=\mathrm{2}{r}^{\mathrm{2}} \left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} −{c}^{\mathrm{2}} \right) \\ $$
