Question Number 83558 by Jidda28 last updated on 03/Mar/20

Commented by Jidda28 last updated on 03/Mar/20

$${help}\:{me}\:{out}\:{pls}. \\ $$
Commented by mathmax by abdo last updated on 03/Mar/20
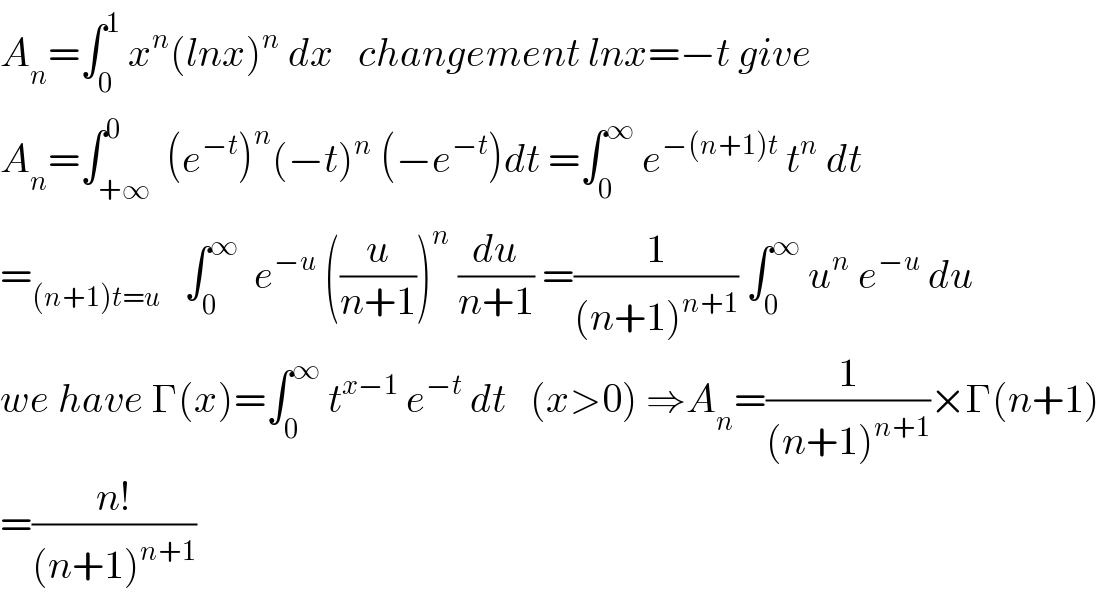
$${A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} \left({lnx}\right)^{{n}} \:{dx}\:\:\:{changement}\:{lnx}=−{t}\:{give} \\ $$$${A}_{{n}} =\int_{+\infty} ^{\mathrm{0}} \:\left({e}^{−{t}} \right)^{{n}} \left(−{t}\right)^{{n}} \:\left(−{e}^{−{t}} \right){dt}\:=\int_{\mathrm{0}} ^{\infty} \:{e}^{−\left({n}+\mathrm{1}\right){t}} \:{t}^{{n}} \:{dt} \\ $$$$=_{\left({n}+\mathrm{1}\right){t}={u}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{u}} \:\left(\frac{{u}}{{n}+\mathrm{1}}\right)^{{n}} \:\frac{{du}}{{n}+\mathrm{1}}\:=\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} }\:\int_{\mathrm{0}} ^{\infty} \:{u}^{{n}} \:{e}^{−{u}} \:{du} \\ $$$${we}\:{have}\:\Gamma\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:{t}^{{x}−\mathrm{1}} \:{e}^{−{t}} \:{dt}\:\:\:\left({x}>\mathrm{0}\right)\:\Rightarrow{A}_{{n}} =\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} }×\Gamma\left({n}+\mathrm{1}\right) \\ $$$$=\frac{{n}!}{\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} } \\ $$
Commented by Jidda28 last updated on 03/Mar/20
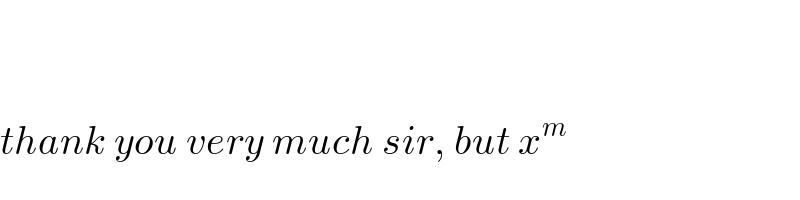
$${thank}\:{you}\:{very}\:{much}\:{sir},\:{but}\:{x}^{{m}\:\overset{} {\:}} \\ $$
Commented by mathmax by abdo last updated on 03/Mar/20

$${you}\:{are}\:{welcome} \\ $$
