Question-83559

Question Number 83559 by Jidda28 last updated on 03/Mar/20

Commented by Jidda28 last updated on 03/Mar/20

$${help}\:{me}\:{out}\:{pls}. \\ $$

Answered by mind is power last updated on 04/Mar/20

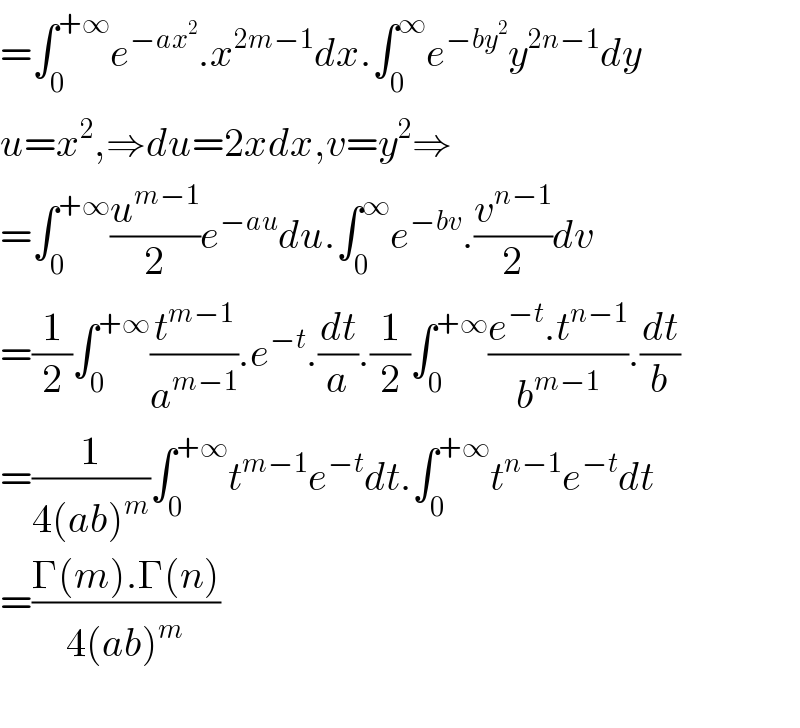
=∫_0 ^(+∞) e^(−ax^2 ) .x^(2m−1) dx.∫_0 ^∞ e^(−by^2 ) y^(2n−1) dy u=x^2 ,⇒du=2xdx,v=y^2 ⇒ =∫_0 ^(+∞) (u^(m−1) /2)e^(−au) du.∫_0 ^∞ e^(−bv) .(v^(n−1) /2)dv =(1/2)∫_0 ^(+∞) (t^(m−1) /a^(m−1) ).e^(−t) .(dt/a).(1/2)∫_0 ^(+∞) ((e^(−t) .t^(n−1) )/b^(m−1) ).(dt/b) =(1/(4(ab)^m ))∫_0 ^(+∞) t^(m−1) e^(−t) dt.∫_0 ^(+∞) t^(n−1) e^(−t) dt =((Γ(m).Γ(n))/(4(ab)^m ))

$$=\int_{\mathrm{0}} ^{+\infty} {e}^{−{ax}^{\mathrm{2}} } .{x}^{\mathrm{2}{m}−\mathrm{1}} {dx}.\int_{\mathrm{0}} ^{\infty} {e}^{−{by}^{\mathrm{2}} } {y}^{\mathrm{2}{n}−\mathrm{1}} {dy} \\ $$$${u}={x}^{\mathrm{2}} ,\Rightarrow{du}=\mathrm{2}{xdx},{v}={y}^{\mathrm{2}} \Rightarrow \\ $$$$=\int_{\mathrm{0}} ^{+\infty} \frac{{u}^{{m}−\mathrm{1}} }{\mathrm{2}}{e}^{−{au}} {du}.\int_{\mathrm{0}} ^{\infty} {e}^{−{bv}} .\frac{{v}^{{n}−\mathrm{1}} }{\mathrm{2}}{dv} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{+\infty} \frac{{t}^{{m}−\mathrm{1}} }{{a}^{{m}−\mathrm{1}} }.{e}^{−{t}} .\frac{{dt}}{{a}}.\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{+\infty} \frac{{e}^{−{t}} .{t}^{{n}−\mathrm{1}} }{{b}^{{m}−\mathrm{1}} }.\frac{{dt}}{{b}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\left({ab}\right)^{{m}} }\int_{\mathrm{0}} ^{+\infty} {t}^{{m}−\mathrm{1}} {e}^{−{t}} {dt}.\int_{\mathrm{0}} ^{+\infty} {t}^{{n}−\mathrm{1}} {e}^{−{t}} {dt} \\ $$$$=\frac{\Gamma\left({m}\right).\Gamma\left({n}\right)}{\mathrm{4}\left({ab}\right)^{{m}} } \\ $$$$ \\ $$

Commented by Jidda28 last updated on 04/Mar/20

$${thank}\:{you}\:{sir} \\ $$

Facebook Tweet Pin

Question-83559

Leave a Reply Cancel reply