Question Number 83638 by bshahid010@gmail.com last updated on 04/Mar/20
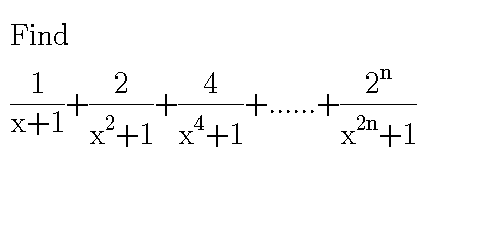
Answered by TANMAY PANACEA last updated on 05/Mar/20
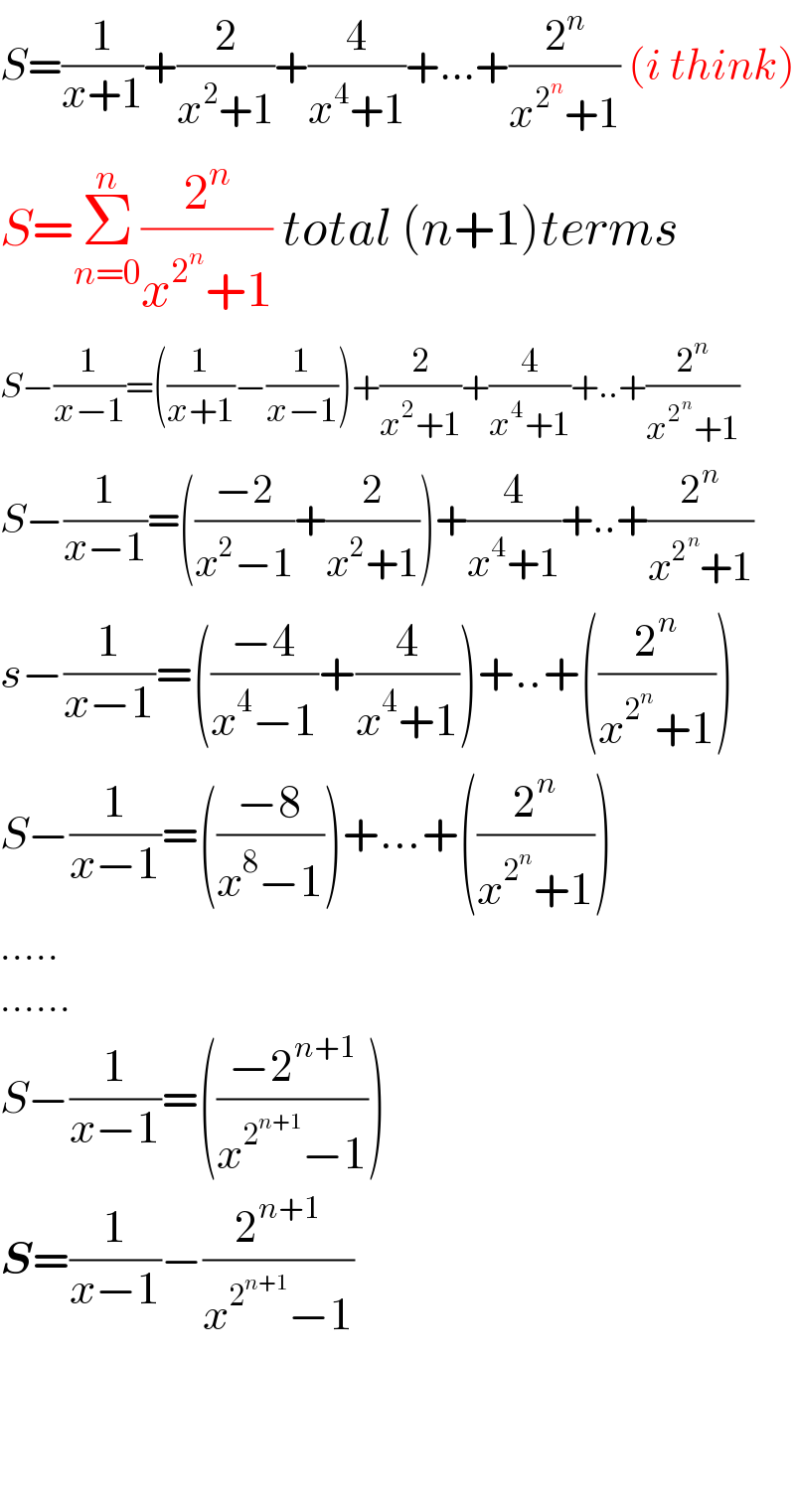
$${S}=\frac{\mathrm{1}}{{x}+\mathrm{1}}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{4}}{{x}^{\mathrm{4}} +\mathrm{1}}+…+\frac{\mathrm{2}^{{n}} }{{x}^{\mathrm{2}^{{n}} } +\mathrm{1}}\:\left({i}\:{think}\right) \\ $$$${S}=\underset{{n}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{2}^{{n}} }{{x}^{\mathrm{2}^{{n}} } +\mathrm{1}}\:{total}\:\left({n}+\mathrm{1}\right){terms} \\ $$$${S}−\frac{\mathrm{1}}{{x}−\mathrm{1}}=\left(\frac{\mathrm{1}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{{x}−\mathrm{1}}\right)+\frac{\mathrm{2}}{{x}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{4}}{{x}^{\mathrm{4}} +\mathrm{1}}+..+\frac{\mathrm{2}^{{n}} }{{x}^{\mathrm{2}^{{n}} } +\mathrm{1}} \\ $$$${S}−\frac{\mathrm{1}}{{x}−\mathrm{1}}=\left(\frac{−\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{1}}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} +\mathrm{1}}\right)+\frac{\mathrm{4}}{{x}^{\mathrm{4}} +\mathrm{1}}+..+\frac{\mathrm{2}^{{n}} }{{x}^{\mathrm{2}^{{n}} } +\mathrm{1}} \\ $$$${s}−\frac{\mathrm{1}}{{x}−\mathrm{1}}=\left(\frac{−\mathrm{4}}{{x}^{\mathrm{4}} −\mathrm{1}}+\frac{\mathrm{4}}{{x}^{\mathrm{4}} +\mathrm{1}}\right)+..+\left(\frac{\mathrm{2}^{{n}} }{{x}^{\mathrm{2}^{{n}} } +\mathrm{1}}\right) \\ $$$${S}−\frac{\mathrm{1}}{{x}−\mathrm{1}}=\left(\frac{−\mathrm{8}}{{x}^{\mathrm{8}} −\mathrm{1}}\right)+…+\left(\frac{\mathrm{2}^{{n}} }{{x}^{\mathrm{2}^{{n}} } +\mathrm{1}}\right) \\ $$$$….. \\ $$$$…… \\ $$$${S}−\frac{\mathrm{1}}{{x}−\mathrm{1}}=\left(\frac{−\mathrm{2}^{{n}+\mathrm{1}} }{{x}^{\mathrm{2}^{{n}+\mathrm{1}} } −\mathrm{1}}\right) \\ $$$$\boldsymbol{{S}}=\frac{\mathrm{1}}{{x}−\mathrm{1}}−\frac{\mathrm{2}^{{n}+\mathrm{1}} }{{x}^{\mathrm{2}^{{n}+\mathrm{1}} } −\mathrm{1}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
