Question Number 83649 by 698148290 last updated on 04/Mar/20
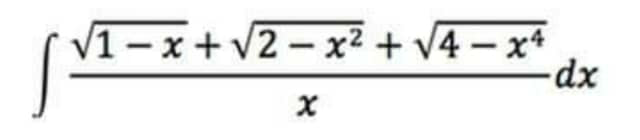
Answered by MJS last updated on 05/Mar/20

$$=\int\frac{\sqrt{\mathrm{1}−{x}}}{{x}}{dx}+\int\frac{\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }}{{x}}{dx}+\int\frac{\sqrt{\mathrm{4}−{x}^{\mathrm{4}} }}{{x}}{dx} \\ $$$$\mathrm{substitute} \\ $$$${u}=\sqrt{\mathrm{1}−{x}}\:\rightarrow\:{dx}=−\mathrm{2}\sqrt{\mathrm{1}−{x}}{du} \\ $$$${v}=\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }\:\rightarrow\:{dx}=−\frac{\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }}{{x}}{dv} \\ $$$${w}=\sqrt{\mathrm{4}−{x}^{\mathrm{4}} }\:\rightarrow\:{dx}=−\frac{\sqrt{\mathrm{4}−{x}^{\mathrm{4}} }}{\mathrm{2}{x}^{\mathrm{3}} }{dw} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{rest}\:\mathrm{is}\:\mathrm{easy} \\ $$
