Question Number 83674 by Power last updated on 05/Mar/20

Commented by Power last updated on 05/Mar/20

$$\mathrm{sir}\:\:\mathrm{MJS} \\ $$
Answered by mahdi last updated on 05/Mar/20
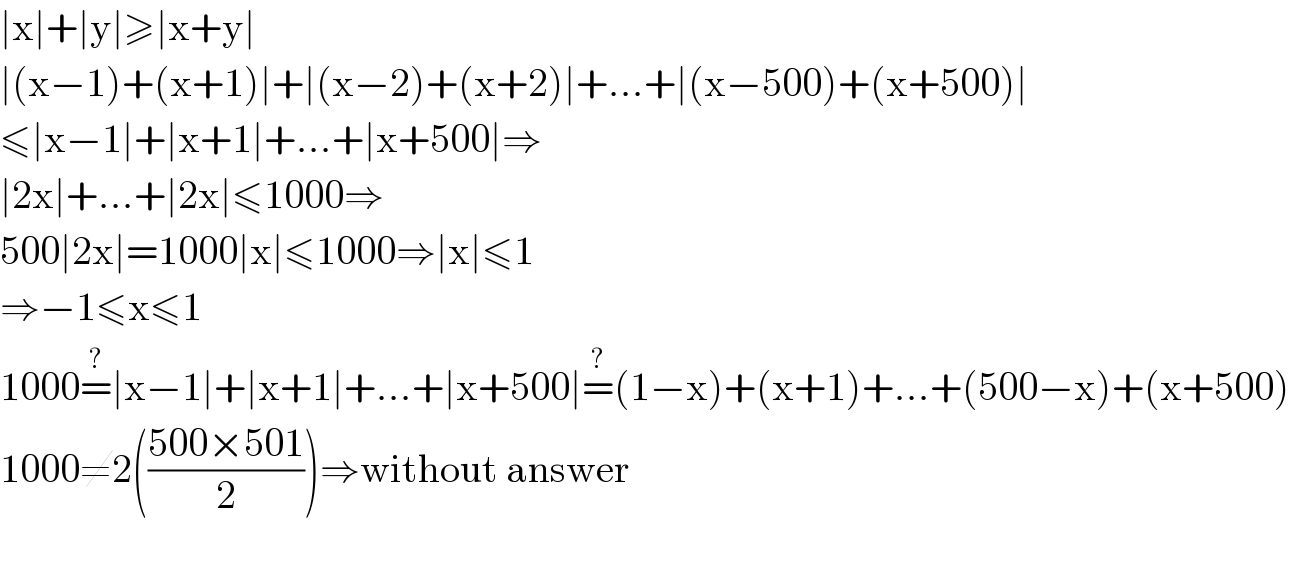
$$\mid\mathrm{x}\mid+\mid\mathrm{y}\mid\geqslant\mid\mathrm{x}+\mathrm{y}\mid \\ $$$$\mid\left(\mathrm{x}−\mathrm{1}\right)+\left(\mathrm{x}+\mathrm{1}\right)\mid+\mid\left(\mathrm{x}−\mathrm{2}\right)+\left(\mathrm{x}+\mathrm{2}\right)\mid+…+\mid\left(\mathrm{x}−\mathrm{500}\right)+\left(\mathrm{x}+\mathrm{500}\right)\mid \\ $$$$\leqslant\mid\mathrm{x}−\mathrm{1}\mid+\mid\mathrm{x}+\mathrm{1}\mid+…+\mid\mathrm{x}+\mathrm{500}\mid\Rightarrow \\ $$$$\mid\mathrm{2x}\mid+…+\mid\mathrm{2x}\mid\leqslant\mathrm{1000}\Rightarrow \\ $$$$\mathrm{500}\mid\mathrm{2x}\mid=\mathrm{1000}\mid\mathrm{x}\mid\leqslant\mathrm{1000}\Rightarrow\mid\mathrm{x}\mid\leqslant\mathrm{1} \\ $$$$\Rightarrow−\mathrm{1}\leqslant\mathrm{x}\leqslant\mathrm{1} \\ $$$$\mathrm{1000}\overset{?} {=}\mid\mathrm{x}−\mathrm{1}\mid+\mid\mathrm{x}+\mathrm{1}\mid+…+\mid\mathrm{x}+\mathrm{500}\mid\overset{?} {=}\left(\mathrm{1}−\mathrm{x}\right)+\left(\mathrm{x}+\mathrm{1}\right)+…+\left(\mathrm{500}−\mathrm{x}\right)+\left(\mathrm{x}+\mathrm{500}\right) \\ $$$$\mathrm{1000}\neq\mathrm{2}\left(\frac{\mathrm{500}×\mathrm{501}}{\mathrm{2}}\right)\Rightarrow\mathrm{without}\:\mathrm{answer} \\ $$$$ \\ $$
