Question Number 83680 by Power last updated on 05/Mar/20
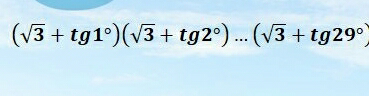
Commented by john santu last updated on 05/Mar/20

$$\mathrm{considering}\:\mathrm{A}+\mathrm{B}\:=\:\mathrm{30}^{\mathrm{o}} \\ $$$$\mathrm{B}\:=\:\mathrm{30}^{\mathrm{o}} −\mathrm{A}\:\Rightarrow\:\mathrm{tan}\:\mathrm{B}\:=\:\frac{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}−\mathrm{tan}\:\mathrm{A}}{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\mathrm{tan}\:\mathrm{A}} \\ $$$$\mathrm{tan}\:\mathrm{B}\:=\:\frac{\mathrm{1}−\sqrt{\mathrm{3}}\:\mathrm{tan}\:\mathrm{A}}{\:\sqrt{\mathrm{3}}+\mathrm{tan}\:\mathrm{A}} \\ $$$$\sqrt{\mathrm{3}}\:+\:\mathrm{tan}\:\mathrm{B}\:=\:\sqrt{\mathrm{3}}+\frac{\mathrm{1}−\sqrt{\mathrm{3}}\:\mathrm{tan}\:\mathrm{A}}{\:\sqrt{\mathrm{3}}+\mathrm{tan}\:\mathrm{A}} \\ $$$$=\:\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}+\mathrm{tan}\:\mathrm{A}} \\ $$$$\mathrm{now}\:\left(\sqrt{\mathrm{3}}+\mathrm{tan}\:\mathrm{A}\right)\left(\sqrt{\mathrm{3}}+\mathrm{tan}\:\mathrm{B}\right)\:= \\ $$$$\left(\sqrt{\mathrm{3}}+\mathrm{tan}\:\mathrm{A}\right)\left(\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}+\mathrm{tan}\:\mathrm{A}}\right)\:=\:\mathrm{4}\: \\ $$$$\mathrm{so}\:\Rightarrow\:\left(\mathrm{4}^{\mathrm{14}} \:\right)\left(\sqrt{\mathrm{3}}\:+\mathrm{tan}\:\mathrm{15}^{\mathrm{o}} \right)\: \\ $$$$\mathrm{i}\:\mathrm{think}\:\mathrm{it}\:\mathrm{easy} \\ $$$$ \\ $$
Commented by jagoll last updated on 05/Mar/20
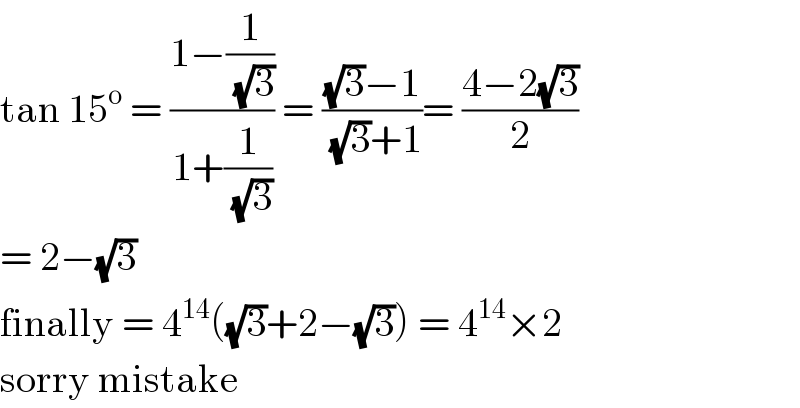
$$\mathrm{tan}\:\mathrm{15}^{\mathrm{o}} \:=\:\frac{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}\:=\:\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\:\sqrt{\mathrm{3}}+\mathrm{1}}=\:\frac{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$=\:\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$$\mathrm{finally}\:=\:\mathrm{4}^{\mathrm{14}} \left(\sqrt{\mathrm{3}}+\mathrm{2}−\sqrt{\mathrm{3}}\right)\:=\:\mathrm{4}^{\mathrm{14}} ×\mathrm{2} \\ $$$$\mathrm{sorry}\:\mathrm{mistake} \\ $$
Commented by MJS last updated on 05/Mar/20
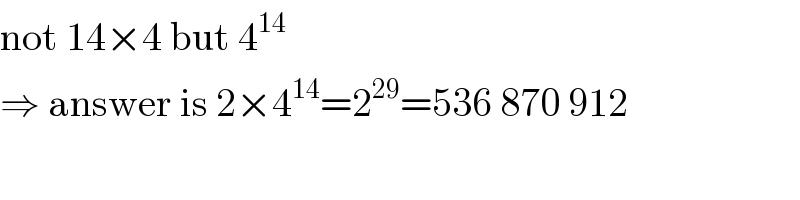
$$\mathrm{not}\:\mathrm{14}×\mathrm{4}\:\mathrm{but}\:\mathrm{4}^{\mathrm{14}} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\mathrm{2}×\mathrm{4}^{\mathrm{14}} =\mathrm{2}^{\mathrm{29}} =\mathrm{536}\:\mathrm{870}\:\mathrm{912} \\ $$
Commented by john santu last updated on 05/Mar/20
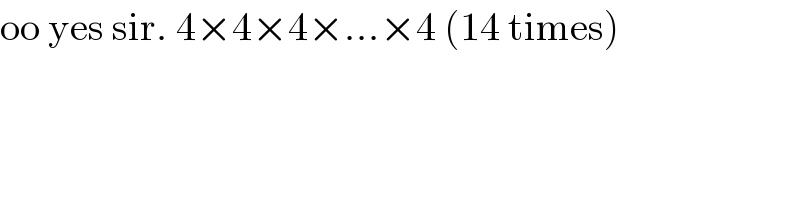
$$\mathrm{oo}\:\mathrm{yes}\:\mathrm{sir}.\:\mathrm{4}×\mathrm{4}×\mathrm{4}×…×\mathrm{4}\:\left(\mathrm{14}\:\mathrm{times}\right) \\ $$
