Menu Close

Question-83721

Tinku Tara 0 Comments
Pin




Question Number 83721 by mr W last updated on 05/Mar/20
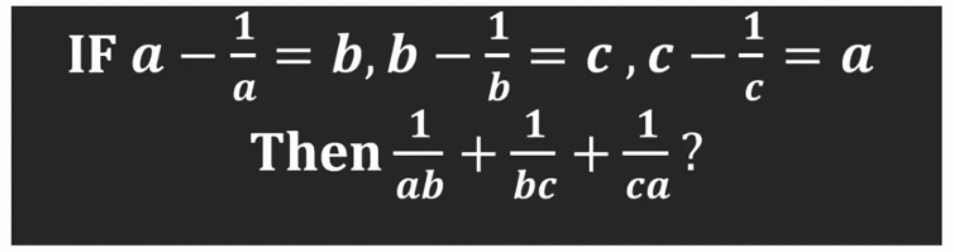
Commented by MJS last updated on 05/Mar/20
−3
−3
Commented by john santu last updated on 05/Mar/20
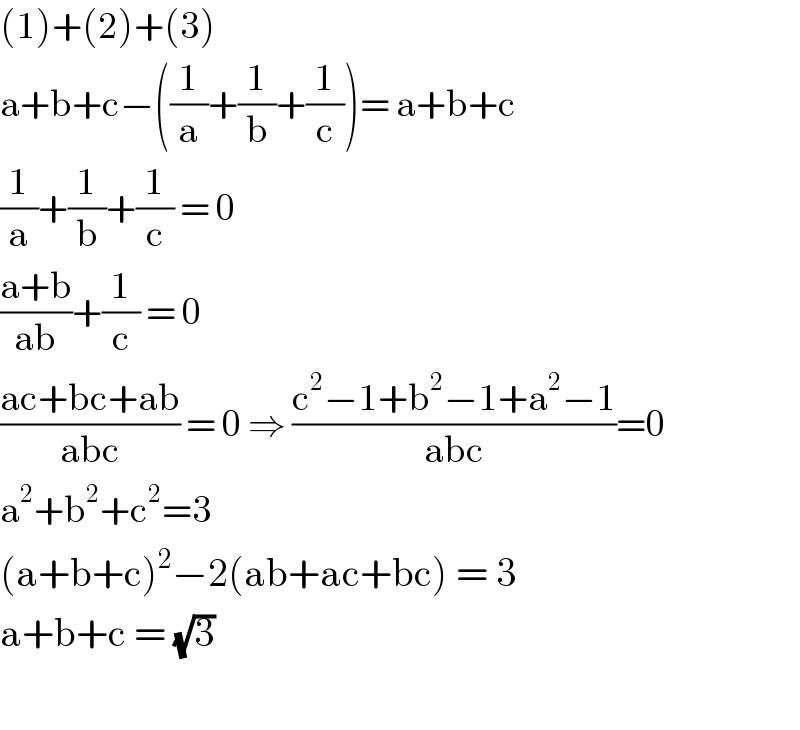
(1)+(2)+(3) a+b+c−((1/a)+(1/b)+(1/c))= a+b+c (1/a)+(1/b)+(1/c) = 0 ((a+b)/(ab))+(1/c) = 0 ((ac+bc+ab)/(abc)) = 0 ⇒ ((c^2 −1+b^2 −1+a^2 −1)/(abc))=0 a^2 +b^2 +c^2 =3 (a+b+c)^2 −2(ab+ac+bc) = 3 a+b+c = (√3)
(1)+(2)+(3)a+b+c−(1a+1b+1c)=a+b+c1a+1b+1c=0a+bab+1c=0ac+bc+ababc=0⇒c2−1+b2−1+a2−1abc=0a2+b2+c2=3(a+b+c)2−2(ab+ac+bc)=3a+b+c=3
Commented by mr W last updated on 05/Mar/20
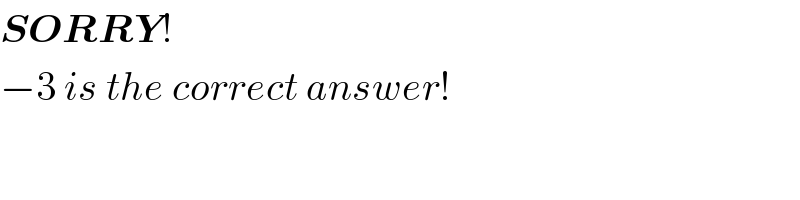
SORRY! −3 is the correct answer!
SORRY!−3isthecorrectanswer!
Commented by john santu last updated on 05/Mar/20
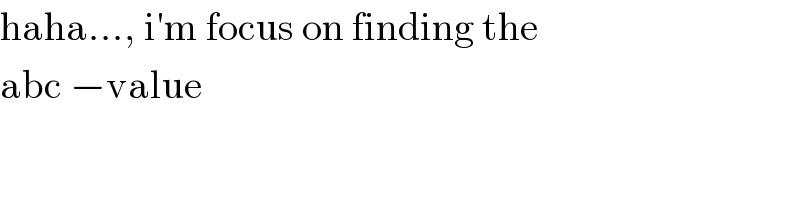
haha..., i′m focus on finding the abc −value
haha…,i′mfocusonfindingtheabc−value
Commented by MJS last updated on 05/Mar/20
(1/a)+(1/b)+(1/c)=0 ⇒ c=−((ab)/(a+b)) (1/(ab))+(1/(bc))+(1/(ca))=0 ⇒ c=−(a+b) −((ab)/(a+b))=−(a+b) ⇒ b=a(−(1/2)±((√3)/2)i) ⇒ c=a(−(1/2)∓((√3)/2)i) b−(1/b)=c ⇒ a^2 =−(1/2)±((√3)/6)i but then a−(1/a)≠b ∧ c−(1/c)≠a
1a+1b+1c=0⇒c=−aba+b1ab+1bc+1ca=0⇒c=−(a+b)−aba+b=−(a+b)⇒b=a(−12±32i)⇒c=a(−12∓32i)b−1b=c⇒a2=−12±36ibutthena−1a≠b∧c−1c≠a
Commented by Prithwish Sen 1 last updated on 05/Mar/20
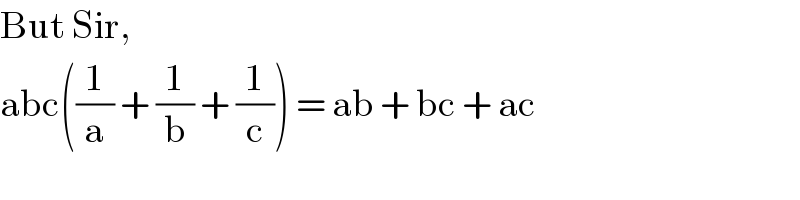
But Sir, abc((1/a) + (1/b) + (1/c)) = ab + bc + ac
ButSir,abc(1a+1b+1c)=ab+bc+ac
Commented by MJS last updated on 05/Mar/20
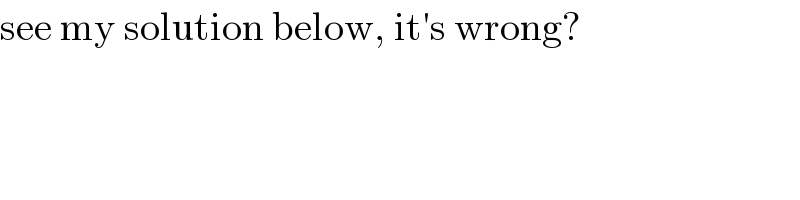
see my solution below, it′s wrong?
seemysolutionbelow,it′swrong?
Commented by Prithwish Sen 1 last updated on 05/Mar/20
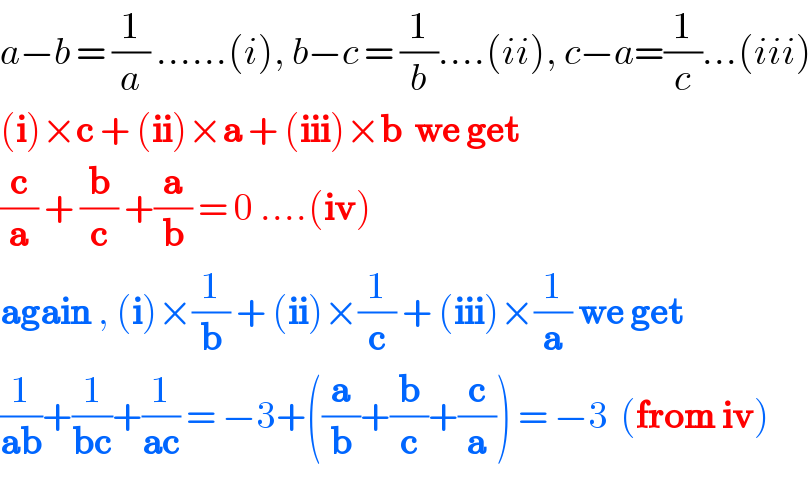
a−b = (1/a) ......(i), b−c = (1/b)....(ii), c−a=(1/c)...(iii) (i)×c + (ii)×a + (iii)×b we get (c/a) + (b/c) +(a/b) = 0 ....(iv) again , (i)×(1/b) + (ii)×(1/c) + (iii)×(1/a) we get (1/(ab))+(1/(bc))+(1/(ac)) = −3+((a/b)+(b/c)+(c/a)) = −3 (from iv)
a−b=1a……(i),b−c=1b….(ii),c−a=1c…(iii)(i)×c+(ii)×a+(iii)×bwegetca+bc+ab=0….(iv)again,(i)×1b+(ii)×1c+(iii)×1aweget1ab+1bc+1ac=−3+(ab+bc+ca)=−3(fromiv)
Answered by MJS last updated on 05/Mar/20
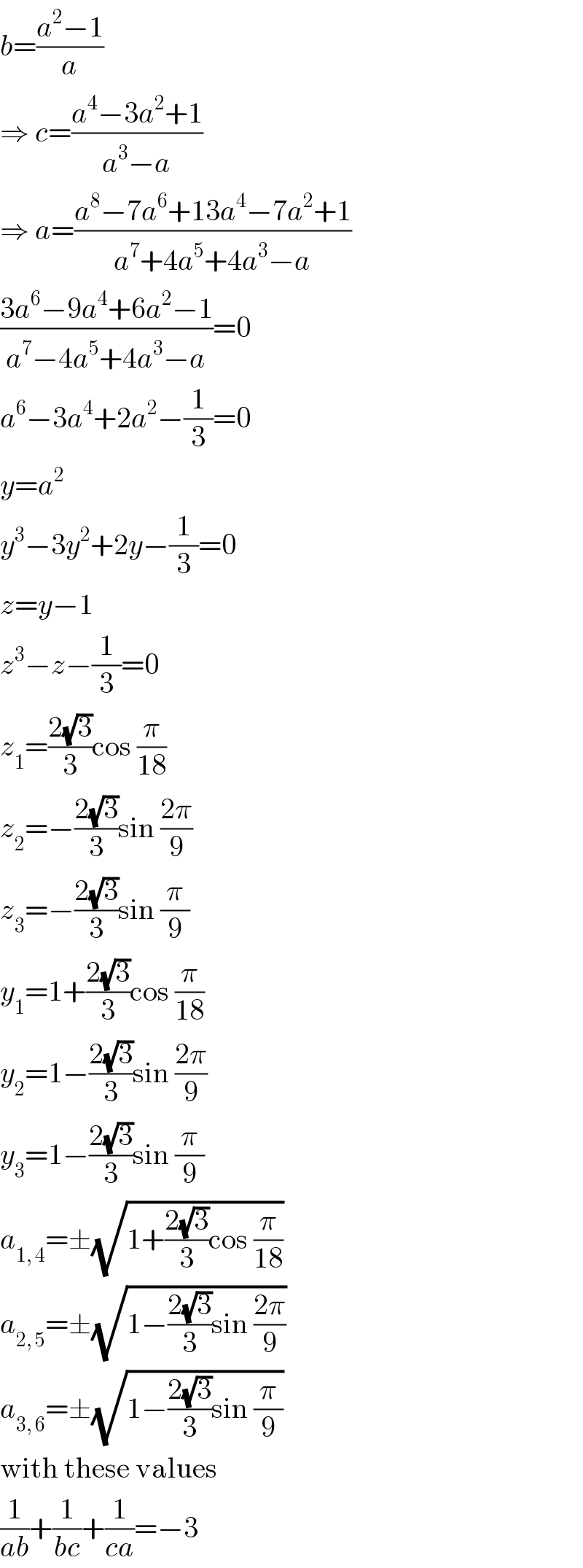
b=((a^2 −1)/a) ⇒ c=((a^4 −3a^2 +1)/(a^3 −a)) ⇒ a=((a^8 −7a^6 +13a^4 −7a^2 +1)/(a^7 +4a^5 +4a^3 −a)) ((3a^6 −9a^4 +6a^2 −1)/(a^7 −4a^5 +4a^3 −a))=0 a^6 −3a^4 +2a^2 −(1/3)=0 y=a^2 y^3 −3y^2 +2y−(1/3)=0 z=y−1 z^3 −z−(1/3)=0 z_1 =((2(√3))/3)cos (π/(18)) z_2 =−((2(√3))/3)sin ((2π)/9) z_3 =−((2(√3))/3)sin (π/9) y_1 =1+((2(√3))/3)cos (π/(18)) y_2 =1−((2(√3))/3)sin ((2π)/9) y_3 =1−((2(√3))/3)sin (π/9) a_(1, 4) =±(√(1+((2(√3))/3)cos (π/(18)))) a_(2, 5) =±(√(1−((2(√3))/3)sin ((2π)/9))) a_(3, 6) =±(√(1−((2(√3))/3)sin (π/9))) with these values (1/(ab))+(1/(bc))+(1/(ca))=−3
b=a2−1a⇒c=a4−3a2+1a3−a⇒a=a8−7a6+13a4−7a2+1a7+4a5+4a3−a3a6−9a4+6a2−1a7−4a5+4a3−a=0a6−3a4+2a2−13=0y=a2y3−3y2+2y−13=0z=y−1z3−z−13=0z1=233cosπ18z2=−233sin2π9z3=−233sinπ9y1=1+233cosπ18y2=1−233sin2π9y3=1−233sinπ9a1,4=±1+233cosπ18a2,5=±1−233sin2π9a3,6=±1−233sinπ9withthesevalues1ab+1bc+1ca=−3
Commented by Prithwish Sen 1 last updated on 05/Mar/20
perfect sir . How r u sir .
perfectsir.Howrusir.
Answered by mr W last updated on 05/Mar/20
Answered by behi83417@gmail.com last updated on 05/Mar/20
(a/b)−(1/(ab))=1,(b/c)−(1/(bc))=1,(c/a)−(1/(ac))=1 ⇒(1/(ab))+(1/(bc))+(1/(ca))=((a/b)+(b/c)+(c/a))−3=−3 [(a/b)+(b/c)+(c/a)=c(a−b)+a(b−c)+b(c−a)=0]
ab−1ab=1,bc−1bc=1,ca−1ac=1⇒1ab+1bc+1ca=(ab+bc+ca)−3=−3[ab+bc+ca=c(a−b)+a(b−c)+b(c−a)=0]

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *