Question Number 83811 by Power last updated on 06/Mar/20
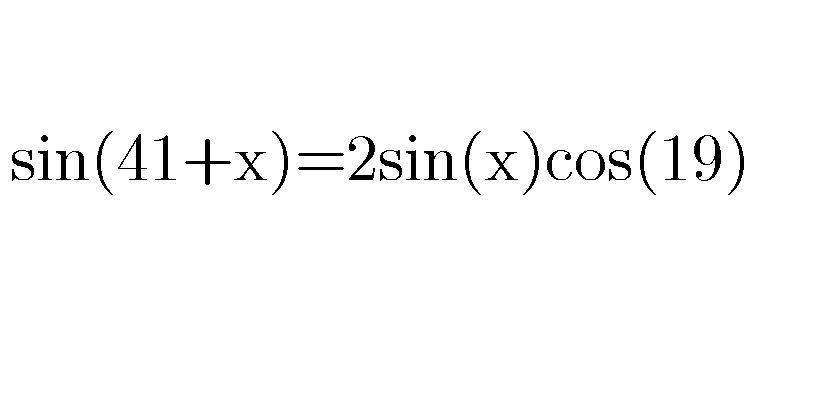
Commented by Power last updated on 06/Mar/20

$$\mathrm{thanks} \\ $$
Commented by john santu last updated on 06/Mar/20
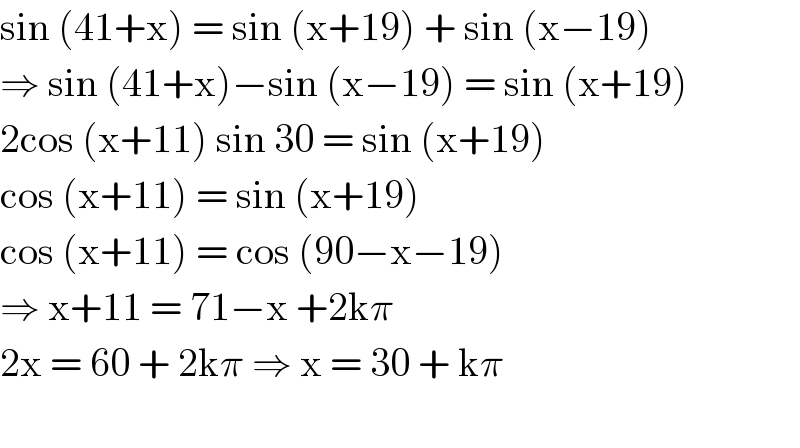
$$\mathrm{sin}\:\left(\mathrm{41}+\mathrm{x}\right)\:=\:\mathrm{sin}\:\left(\mathrm{x}+\mathrm{19}\right)\:+\:\mathrm{sin}\:\left(\mathrm{x}−\mathrm{19}\right) \\ $$$$\Rightarrow\:\mathrm{sin}\:\left(\mathrm{41}+\mathrm{x}\right)−\mathrm{sin}\:\left(\mathrm{x}−\mathrm{19}\right)\:=\:\mathrm{sin}\:\left(\mathrm{x}+\mathrm{19}\right) \\ $$$$\mathrm{2cos}\:\left(\mathrm{x}+\mathrm{11}\right)\:\mathrm{sin}\:\mathrm{30}\:=\:\mathrm{sin}\:\left(\mathrm{x}+\mathrm{19}\right) \\ $$$$\mathrm{cos}\:\left(\mathrm{x}+\mathrm{11}\right)\:=\:\mathrm{sin}\:\left(\mathrm{x}+\mathrm{19}\right) \\ $$$$\mathrm{cos}\:\left(\mathrm{x}+\mathrm{11}\right)\:=\:\mathrm{cos}\:\left(\mathrm{90}−\mathrm{x}−\mathrm{19}\right) \\ $$$$\Rightarrow\:\mathrm{x}+\mathrm{11}\:=\:\mathrm{71}−\mathrm{x}\:+\mathrm{2k}\pi \\ $$$$\mathrm{2x}\:=\:\mathrm{60}\:+\:\mathrm{2k}\pi\:\Rightarrow\:\mathrm{x}\:=\:\mathrm{30}\:+\:\mathrm{k}\pi \\ $$$$ \\ $$
