Question Number 83822 by Power last updated on 06/Mar/20
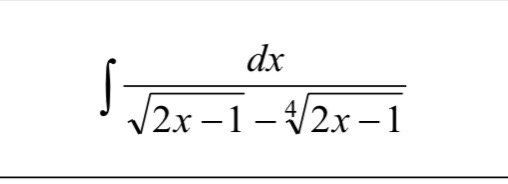
Commented by mathmax by abdo last updated on 07/Mar/20
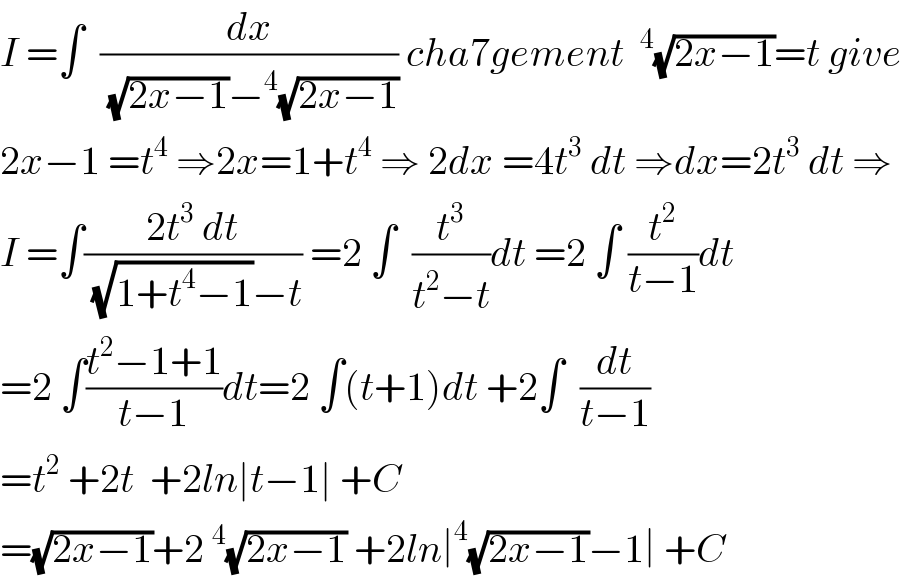
$${I}\:=\int\:\:\frac{{dx}}{\:\sqrt{\mathrm{2}{x}−\mathrm{1}}−^{\mathrm{4}} \sqrt{\mathrm{2}{x}−\mathrm{1}}}\:{cha}\mathrm{7}{gement}\:\:^{\mathrm{4}} \sqrt{\mathrm{2}{x}−\mathrm{1}}={t}\:{give} \\ $$$$\mathrm{2}{x}−\mathrm{1}\:={t}^{\mathrm{4}} \:\Rightarrow\mathrm{2}{x}=\mathrm{1}+{t}^{\mathrm{4}} \:\Rightarrow\:\mathrm{2}{dx}\:=\mathrm{4}{t}^{\mathrm{3}} \:{dt}\:\Rightarrow{dx}=\mathrm{2}{t}^{\mathrm{3}} \:{dt}\:\Rightarrow \\ $$$${I}\:=\int\frac{\mathrm{2}{t}^{\mathrm{3}} \:{dt}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{4}} −\mathrm{1}}−{t}}\:=\mathrm{2}\:\int\:\:\frac{{t}^{\mathrm{3}} }{{t}^{\mathrm{2}} −{t}}{dt}\:=\mathrm{2}\:\int\:\frac{{t}^{\mathrm{2}} }{{t}−\mathrm{1}}{dt} \\ $$$$=\mathrm{2}\:\int\frac{{t}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}}{{t}−\mathrm{1}}{dt}=\mathrm{2}\:\int\left({t}+\mathrm{1}\right){dt}\:+\mathrm{2}\int\:\:\frac{{dt}}{{t}−\mathrm{1}} \\ $$$$={t}^{\mathrm{2}} \:+\mathrm{2}{t}\:\:+\mathrm{2}{ln}\mid{t}−\mathrm{1}\mid\:+{C} \\ $$$$=\sqrt{\mathrm{2}{x}−\mathrm{1}}+\mathrm{2}\:^{\mathrm{4}} \sqrt{\mathrm{2}{x}−\mathrm{1}}\:+\mathrm{2}{ln}\mid^{\mathrm{4}} \sqrt{\mathrm{2}{x}−\mathrm{1}}−\mathrm{1}\mid\:+{C} \\ $$
Answered by john santu last updated on 06/Mar/20
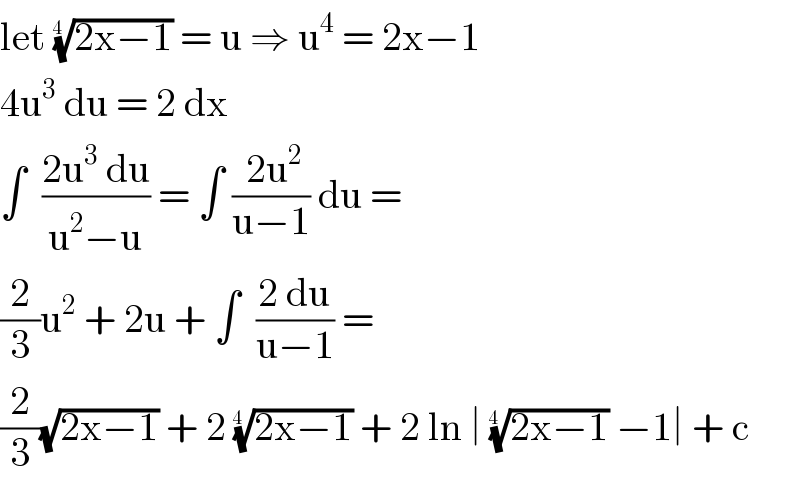
$$\mathrm{let}\:\sqrt[{\mathrm{4}\:\:}]{\mathrm{2x}−\mathrm{1}}\:=\:\mathrm{u}\:\Rightarrow\:\mathrm{u}^{\mathrm{4}} \:=\:\mathrm{2x}−\mathrm{1} \\ $$$$\mathrm{4u}^{\mathrm{3}} \:\mathrm{du}\:=\:\mathrm{2}\:\mathrm{dx}\: \\ $$$$\int\:\:\frac{\mathrm{2u}^{\mathrm{3}} \:\mathrm{du}}{\mathrm{u}^{\mathrm{2}} −\mathrm{u}}\:=\:\int\:\frac{\:\mathrm{2u}^{\mathrm{2}} }{\mathrm{u}−\mathrm{1}}\:\mathrm{du}\:=\: \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\mathrm{u}^{\mathrm{2}} \:+\:\mathrm{2u}\:+\:\int\:\:\frac{\mathrm{2}\:\mathrm{du}}{\mathrm{u}−\mathrm{1}}\:= \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\sqrt{\mathrm{2x}−\mathrm{1}}\:+\:\mathrm{2}\:\sqrt[{\mathrm{4}\:\:}]{\mathrm{2x}−\mathrm{1}}\:+\:\mathrm{2}\:\mathrm{ln}\:\mid\:\sqrt[{\mathrm{4}\:\:}]{\mathrm{2x}−\mathrm{1}}\:−\mathrm{1}\mid\:+\:\mathrm{c} \\ $$
