Question Number 84557 by Power last updated on 14/Mar/20
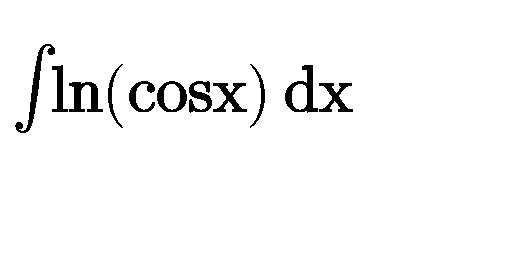
Commented by jagoll last updated on 14/Mar/20
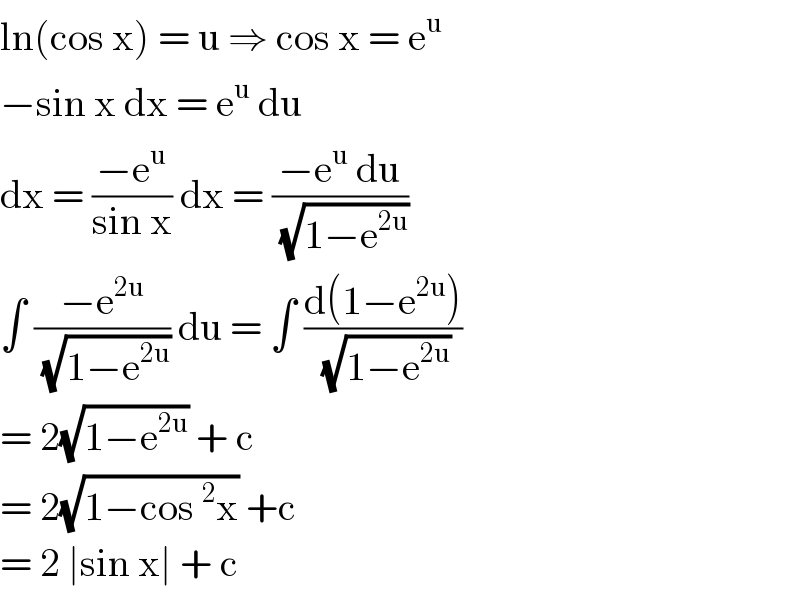
$$\mathrm{ln}\left(\mathrm{cos}\:\mathrm{x}\right)\:=\:\mathrm{u}\:\Rightarrow\:\mathrm{cos}\:\mathrm{x}\:=\:\mathrm{e}^{\mathrm{u}} \\ $$$$−\mathrm{sin}\:\mathrm{x}\:\mathrm{dx}\:=\:\mathrm{e}^{\mathrm{u}} \:\mathrm{du}\: \\ $$$$\mathrm{dx}\:=\:\frac{−\mathrm{e}^{\mathrm{u}} }{\mathrm{sin}\:\mathrm{x}}\:\mathrm{dx}\:=\:\frac{−\mathrm{e}^{\mathrm{u}} \:\mathrm{du}}{\:\sqrt{\mathrm{1}−\mathrm{e}^{\mathrm{2u}} }} \\ $$$$\int\:\frac{−\mathrm{e}^{\mathrm{2u}} }{\:\sqrt{\mathrm{1}−\mathrm{e}^{\mathrm{2u}} }}\:\mathrm{du}\:=\:\int\:\frac{\mathrm{d}\left(\mathrm{1}−\mathrm{e}^{\mathrm{2u}} \right)}{\:\sqrt{\mathrm{1}−\mathrm{e}^{\mathrm{2u}} }} \\ $$$$=\:\mathrm{2}\sqrt{\mathrm{1}−\mathrm{e}^{\mathrm{2u}} }\:+\:\mathrm{c} \\ $$$$=\:\mathrm{2}\sqrt{\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}}\:+\mathrm{c} \\ $$$$=\:\mathrm{2}\:\mid\mathrm{sin}\:\mathrm{x}\mid\:+\:\mathrm{c}\: \\ $$
