Menu Close

Question-85355

Tinku Tara 0 Comments
Pin




Question Number 85355 by TawaTawa1 last updated on 21/Mar/20
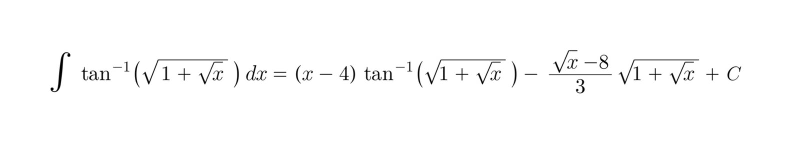
Commented by mathmax by abdo last updated on 21/Mar/20
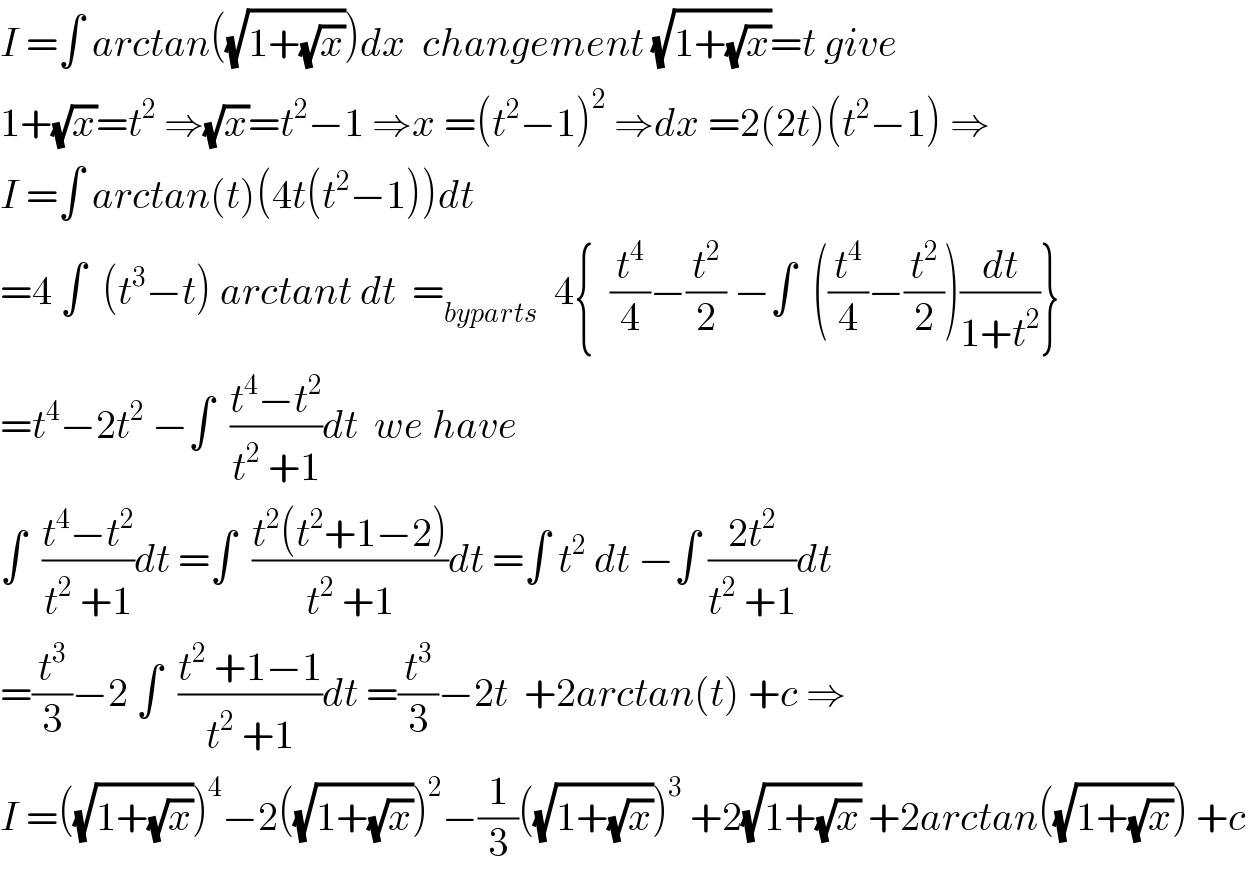
I =∫ arctan((√(1+(√x))))dx changement (√(1+(√x)))=t give 1+(√x)=t^2 ⇒(√x)=t^2 −1 ⇒x =(t^2 −1)^2 ⇒dx =2(2t)(t^2 −1) ⇒ I =∫ arctan(t)(4t(t^2 −1))dt =4 ∫ (t^3 −t) arctant dt =_(byparts) 4{ (t^4 /4)−(t^2 /2) −∫ ((t^4 /4)−(t^2 /2))(dt/(1+t^2 ))} =t^4 −2t^2 −∫ ((t^4 −t^2 )/(t^2 +1))dt we have ∫ ((t^4 −t^2 )/(t^2 +1))dt =∫ ((t^2 (t^2 +1−2))/(t^2 +1))dt =∫ t^2 dt −∫ ((2t^2 )/(t^2 +1))dt =(t^3 /3)−2 ∫ ((t^2 +1−1)/(t^2 +1))dt =(t^3 /3)−2t +2arctan(t) +c ⇒ I =((√(1+(√x))))^4 −2((√(1+(√x))))^2 −(1/3)((√(1+(√x))))^3 +2(√(1+(√x))) +2arctan((√(1+(√x)))) +c
$${I}\:=\int\:{arctan}\left(\sqrt{\mathrm{1}+\sqrt{{x}}}\right){dx}\:\:{changement}\:\sqrt{\mathrm{1}+\sqrt{{x}}}={t}\:{give} \\ $$$$\mathrm{1}+\sqrt{{x}}={t}^{\mathrm{2}} \:\Rightarrow\sqrt{{x}}={t}^{\mathrm{2}} −\mathrm{1}\:\Rightarrow{x}\:=\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \:\Rightarrow{dx}\:=\mathrm{2}\left(\mathrm{2}{t}\right)\left({t}^{\mathrm{2}} −\mathrm{1}\right)\:\Rightarrow \\ $$$${I}\:=\int\:{arctan}\left({t}\right)\left(\mathrm{4}{t}\left({t}^{\mathrm{2}} −\mathrm{1}\right)\right){dt} \\ $$$$=\mathrm{4}\:\int\:\:\left({t}^{\mathrm{3}} −{t}\right)\:{arctant}\:{dt}\:\:=_{{byparts}} \:\:\mathrm{4}\left\{\:\:\frac{{t}^{\mathrm{4}} }{\mathrm{4}}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\:−\int\:\:\left(\frac{{t}^{\mathrm{4}} }{\mathrm{4}}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\right)\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\right\} \\ $$$$={t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} \:−\int\:\:\frac{{t}^{\mathrm{4}} −{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} \:+\mathrm{1}}{dt}\:\:{we}\:{have} \\ $$$$\int\:\:\frac{{t}^{\mathrm{4}} −{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} \:+\mathrm{1}}{dt}\:=\int\:\:\frac{{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}\right)}{{t}^{\mathrm{2}} \:+\mathrm{1}}{dt}\:=\int\:{t}^{\mathrm{2}} \:{dt}\:−\int\:\frac{\mathrm{2}{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} \:+\mathrm{1}}{dt} \\ $$$$=\frac{{t}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{2}\:\int\:\:\frac{{t}^{\mathrm{2}} \:+\mathrm{1}−\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}{dt}\:=\frac{{t}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{2}{t}\:\:+\mathrm{2}{arctan}\left({t}\right)\:+{c}\:\Rightarrow \\ $$$${I}\:=\left(\sqrt{\mathrm{1}+\sqrt{{x}}}\right)^{\mathrm{4}} −\mathrm{2}\left(\sqrt{\mathrm{1}+\sqrt{{x}}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}\left(\sqrt{\mathrm{1}+\sqrt{{x}}}\right)^{\mathrm{3}} \:+\mathrm{2}\sqrt{\mathrm{1}+\sqrt{{x}}}\:+\mathrm{2}{arctan}\left(\sqrt{\mathrm{1}+\sqrt{{x}}}\right)\:+{c} \\ $$
Commented by mathmax by abdo last updated on 21/Mar/20
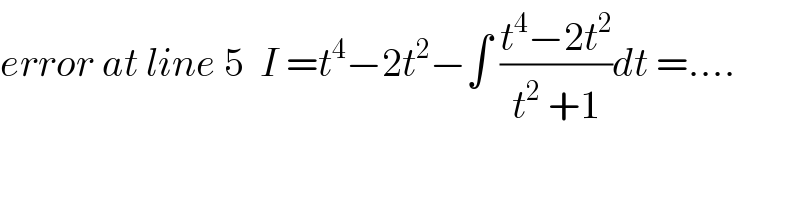
error at line 5 I =t^4 −2t^2 −∫ ((t^4 −2t^2 )/(t^2 +1))dt =....
$${error}\:{at}\:{line}\:\mathrm{5}\:\:{I}\:={t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} −\int\:\frac{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} \:+\mathrm{1}}{dt}\:=…. \\ $$
Commented by TawaTawa1 last updated on 22/Mar/20
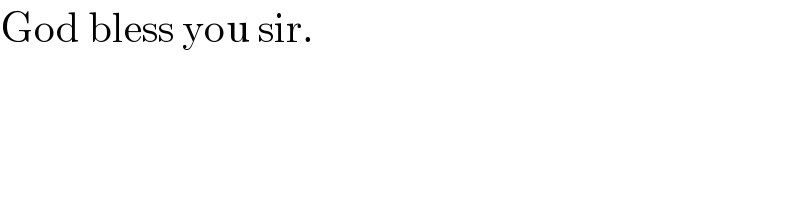
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by abdomathmax last updated on 23/Mar/20
you are welcome miss.
$${you}\:{are}\:{welcome}\:{miss}. \\ $$
Answered by mind is power last updated on 21/Mar/20
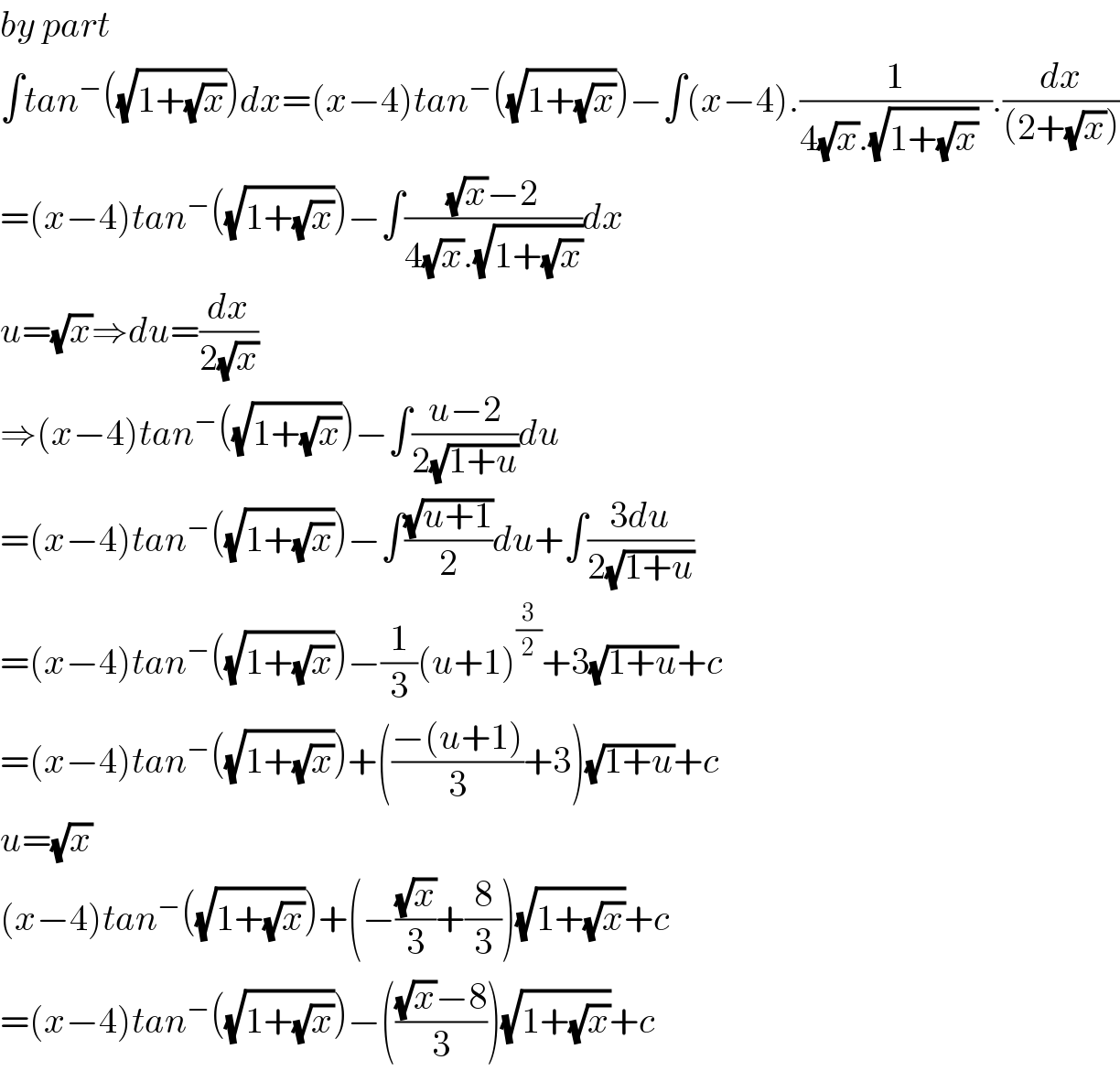
by part ∫tan^− ((√(1+(√x))))dx=(x−4)tan^− ((√(1+(√x))))−∫(x−4).(1/(4(√x).(√(1+(√x))) )).(dx/((2+(√x)))) =(x−4)tan^− ((√(1+(√x))))−∫(((√x)−2)/(4(√x).(√(1+(√x)))))dx u=(√x)⇒du=(dx/(2(√x))) ⇒(x−4)tan^− ((√(1+(√x))))−∫((u−2)/(2(√(1+u))))du =(x−4)tan^− ((√(1+(√x))))−∫((√(u+1))/2)du+∫((3du)/(2(√(1+u)))) =(x−4)tan^− ((√(1+(√x))))−(1/3)(u+1)^(3/2) +3(√(1+u))+c =(x−4)tan^− ((√(1+(√x))))+(((−(u+1))/3)+3)(√(1+u))+c u=(√x) (x−4)tan^− ((√(1+(√x))))+(−((√x)/3)+(8/3))(√(1+(√x)))+c =(x−4)tan^− ((√(1+(√x))))−((((√x)−8)/3))(√(1+(√x)))+c
$${by}\:{part} \\ $$$$\int{tan}^{−} \left(\sqrt{\mathrm{1}+\sqrt{{x}}}\right){dx}=\left({x}−\mathrm{4}\right){tan}^{−} \left(\sqrt{\mathrm{1}+\sqrt{{x}}}\right)−\int\left({x}−\mathrm{4}\right).\frac{\mathrm{1}}{\mathrm{4}\sqrt{{x}}.\sqrt{\mathrm{1}+\sqrt{{x}}}\:\:}.\frac{{dx}}{\left(\mathrm{2}+\sqrt{{x}}\right)} \\ $$$$=\left({x}−\mathrm{4}\right){tan}^{−} \left(\sqrt{\mathrm{1}+\sqrt{{x}}}\right)−\int\frac{\sqrt{{x}}−\mathrm{2}}{\mathrm{4}\sqrt{{x}}.\sqrt{\mathrm{1}+\sqrt{{x}}}}{dx} \\ $$$${u}=\sqrt{{x}}\Rightarrow{du}=\frac{{dx}}{\mathrm{2}\sqrt{{x}}} \\ $$$$\Rightarrow\left({x}−\mathrm{4}\right){tan}^{−} \left(\sqrt{\mathrm{1}+\sqrt{{x}}}\right)−\int\frac{{u}−\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{1}+{u}}}{du} \\ $$$$=\left({x}−\mathrm{4}\right){tan}^{−} \left(\sqrt{\mathrm{1}+\sqrt{{x}}}\right)−\int\frac{\sqrt{{u}+\mathrm{1}}}{\mathrm{2}}{du}+\int\frac{\mathrm{3}{du}}{\mathrm{2}\sqrt{\mathrm{1}+{u}}} \\ $$$$=\left({x}−\mathrm{4}\right){tan}^{−} \left(\sqrt{\mathrm{1}+\sqrt{{x}}}\right)−\frac{\mathrm{1}}{\mathrm{3}}\left({u}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\mathrm{3}\sqrt{\mathrm{1}+{u}}+{c} \\ $$$$=\left({x}−\mathrm{4}\right){tan}^{−} \left(\sqrt{\mathrm{1}+\sqrt{{x}}}\right)+\left(\frac{−\left({u}+\mathrm{1}\right)}{\mathrm{3}}+\mathrm{3}\right)\sqrt{\mathrm{1}+{u}}+{c} \\ $$$${u}=\sqrt{{x}} \\ $$$$\left({x}−\mathrm{4}\right){tan}^{−} \left(\sqrt{\mathrm{1}+\sqrt{{x}}}\right)+\left(−\frac{\sqrt{{x}}}{\mathrm{3}}+\frac{\mathrm{8}}{\mathrm{3}}\right)\sqrt{\mathrm{1}+\sqrt{{x}}}+{c} \\ $$$$=\left({x}−\mathrm{4}\right){tan}^{−} \left(\sqrt{\mathrm{1}+\sqrt{{x}}}\right)−\left(\frac{\sqrt{{x}}−\mathrm{8}}{\mathrm{3}}\right)\sqrt{\mathrm{1}+\sqrt{{x}}}+{c} \\ $$
Commented by TawaTawa1 last updated on 21/Mar/20
God bless you sir, i appreciate your time.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}. \\ $$
Commented by mind is power last updated on 23/Mar/20
withe Pleasur miss
$${withe}\:{Pleasur}\:{miss} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *