Menu Close

Question-85365

Tinku Tara 0 Comments
Pin




Question Number 85365 by Power last updated on 21/Mar/20
Answered by jagoll last updated on 21/Mar/20
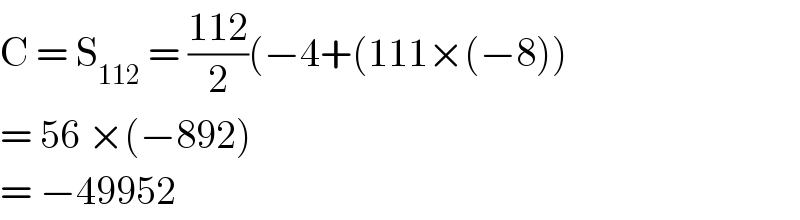
C = S_(112) = ((112)/2)(−4+(111×(−8)) = 56 ×(−892) = −49952
$$\mathrm{C}\:=\:\mathrm{S}_{\mathrm{112}} \:=\:\frac{\mathrm{112}}{\mathrm{2}}\left(−\mathrm{4}+\left(\mathrm{111}×\left(−\mathrm{8}\right)\right)\right. \\ $$$$=\:\mathrm{56}\:×\left(−\mathrm{892}\right) \\ $$$$=\:−\mathrm{49952} \\ $$
Commented by Power last updated on 21/Mar/20
?
$$? \\ $$
Commented by john santu last updated on 21/Mar/20
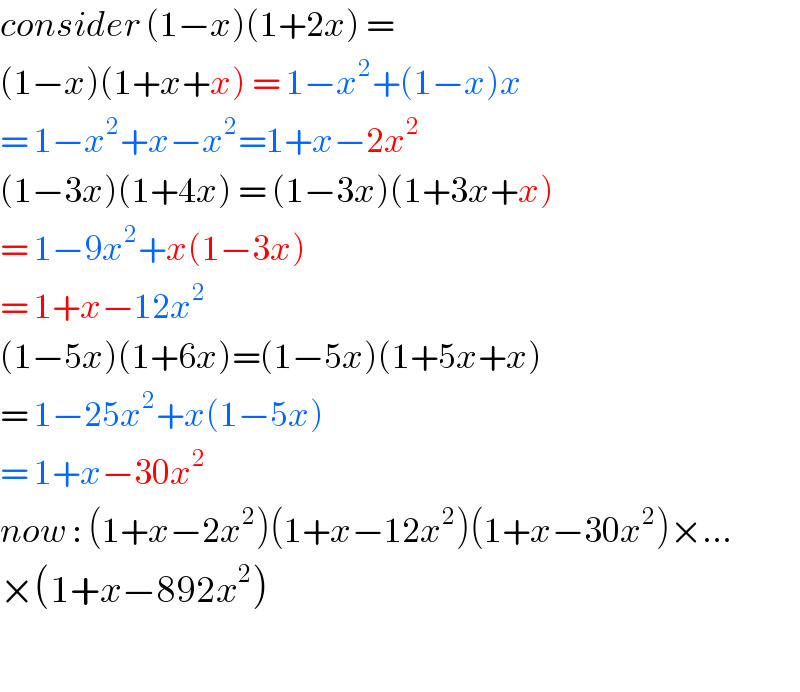
consider (1−x)(1+2x) = (1−x)(1+x+x) = 1−x^2 +(1−x)x = 1−x^2 +x−x^2 =1+x−2x^2 (1−3x)(1+4x) = (1−3x)(1+3x+x) = 1−9x^2 +x(1−3x) = 1+x−12x^2 (1−5x)(1+6x)=(1−5x)(1+5x+x) = 1−25x^2 +x(1−5x) = 1+x−30x^2 now : (1+x−2x^2 )(1+x−12x^2 )(1+x−30x^2 )×... ×(1+x−892x^2 )
$${consider}\:\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+\mathrm{2}{x}\right)\:=\: \\ $$$$\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+{x}+{x}\right)\:=\:\mathrm{1}−{x}^{\mathrm{2}} +\left(\mathrm{1}−{x}\right){x} \\ $$$$=\:\mathrm{1}−{x}^{\mathrm{2}} +{x}−{x}^{\mathrm{2}} =\mathrm{1}+{x}−\mathrm{2}{x}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}−\mathrm{3}{x}\right)\left(\mathrm{1}+\mathrm{4}{x}\right)\:=\:\left(\mathrm{1}−\mathrm{3}{x}\right)\left(\mathrm{1}+\mathrm{3}{x}+{x}\right) \\ $$$$=\:\mathrm{1}−\mathrm{9}{x}^{\mathrm{2}} +{x}\left(\mathrm{1}−\mathrm{3}{x}\right) \\ $$$$=\:\mathrm{1}+{x}−\mathrm{12}{x}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}−\mathrm{5}{x}\right)\left(\mathrm{1}+\mathrm{6}{x}\right)=\left(\mathrm{1}−\mathrm{5}{x}\right)\left(\mathrm{1}+\mathrm{5}{x}+{x}\right) \\ $$$$=\:\mathrm{1}−\mathrm{25}{x}^{\mathrm{2}} +{x}\left(\mathrm{1}−\mathrm{5}{x}\right) \\ $$$$=\:\mathrm{1}+{x}−\mathrm{30}{x}^{\mathrm{2}} \\ $$$${now}\::\:\left(\mathrm{1}+{x}−\mathrm{2}{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}−\mathrm{12}{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}−\mathrm{30}{x}^{\mathrm{2}} \right)×… \\ $$$$×\left(\mathrm{1}+{x}−\mathrm{892}{x}^{\mathrm{2}} \right) \\ $$$$ \\ $$
Commented by Power last updated on 21/Mar/20
i do not understand
$$\mathrm{i}\:\mathrm{do}\:\mathrm{not}\:\mathrm{understand} \\ $$
Commented by john santu last updated on 21/Mar/20
ouwh
$${ouwh} \\ $$
Answered by mr W last updated on 21/Mar/20
(1−(2n−1)x)(1+2nx)=1+x−2n(2n−1)x^2 {(1−x)(1+2x)(1−3x)(1+4x)...(1−221x)(1+222x)}(1−223x) ={Π_(n=1) ^(111) [1−(2n−1)x](1+2nx)}(1−223x) ={Π_(n=1) ^(111) [1+x−2n(2n−1)x^2 ]}(1−223x) coef. of x^2 : −Σ_(n=1) ^(111) 2n(2n−1)+((111×110)/2)−223×111 =−Σ_(n=1) ^(111) (4n^2 −2n)+((111×110)/2)−223×111 =−(4×((111×112×223)/6)−2×((111×112)/2))+((111×110)/2)−223×111 =−4×((111×112×223)/6)−56×111 =−1 854 440 ⇒ answer
$$\left(\mathrm{1}−\left(\mathrm{2}{n}−\mathrm{1}\right){x}\right)\left(\mathrm{1}+\mathrm{2}{nx}\right)=\mathrm{1}+{x}−\mathrm{2}{n}\left(\mathrm{2}{n}−\mathrm{1}\right){x}^{\mathrm{2}} \\ $$$$ \\ $$$$\left\{\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+\mathrm{2}{x}\right)\left(\mathrm{1}−\mathrm{3}{x}\right)\left(\mathrm{1}+\mathrm{4}{x}\right)…\left(\mathrm{1}−\mathrm{221}{x}\right)\left(\mathrm{1}+\mathrm{222}{x}\right)\right\}\left(\mathrm{1}−\mathrm{223}{x}\right) \\ $$$$=\left\{\underset{{n}=\mathrm{1}} {\overset{\mathrm{111}} {\prod}}\left[\mathrm{1}−\left(\mathrm{2}{n}−\mathrm{1}\right){x}\right]\left(\mathrm{1}+\mathrm{2}{nx}\right)\right\}\left(\mathrm{1}−\mathrm{223}{x}\right) \\ $$$$=\left\{\underset{{n}=\mathrm{1}} {\overset{\mathrm{111}} {\prod}}\left[\mathrm{1}+{x}−\mathrm{2}{n}\left(\mathrm{2}{n}−\mathrm{1}\right){x}^{\mathrm{2}} \right]\right\}\left(\mathrm{1}−\mathrm{223}{x}\right) \\ $$$${coef}.\:{of}\:{x}^{\mathrm{2}} : \\ $$$$−\underset{{n}=\mathrm{1}} {\overset{\mathrm{111}} {\sum}}\mathrm{2}{n}\left(\mathrm{2}{n}−\mathrm{1}\right)+\frac{\mathrm{111}×\mathrm{110}}{\mathrm{2}}−\mathrm{223}×\mathrm{111} \\ $$$$=−\underset{{n}=\mathrm{1}} {\overset{\mathrm{111}} {\sum}}\left(\mathrm{4}{n}^{\mathrm{2}} −\mathrm{2}{n}\right)+\frac{\mathrm{111}×\mathrm{110}}{\mathrm{2}}−\mathrm{223}×\mathrm{111} \\ $$$$=−\left(\mathrm{4}×\frac{\mathrm{111}×\mathrm{112}×\mathrm{223}}{\mathrm{6}}−\mathrm{2}×\frac{\mathrm{111}×\mathrm{112}}{\mathrm{2}}\right)+\frac{\mathrm{111}×\mathrm{110}}{\mathrm{2}}−\mathrm{223}×\mathrm{111} \\ $$$$=−\mathrm{4}×\frac{\mathrm{111}×\mathrm{112}×\mathrm{223}}{\mathrm{6}}−\mathrm{56}×\mathrm{111} \\ $$$$=−\mathrm{1}\:\mathrm{854}\:\mathrm{440}\:\Rightarrow\:{answer} \\ $$
Commented by Power last updated on 21/Mar/20
thanks
$$\mathrm{thanks} \\ $$
Answered by mr W last updated on 21/Mar/20
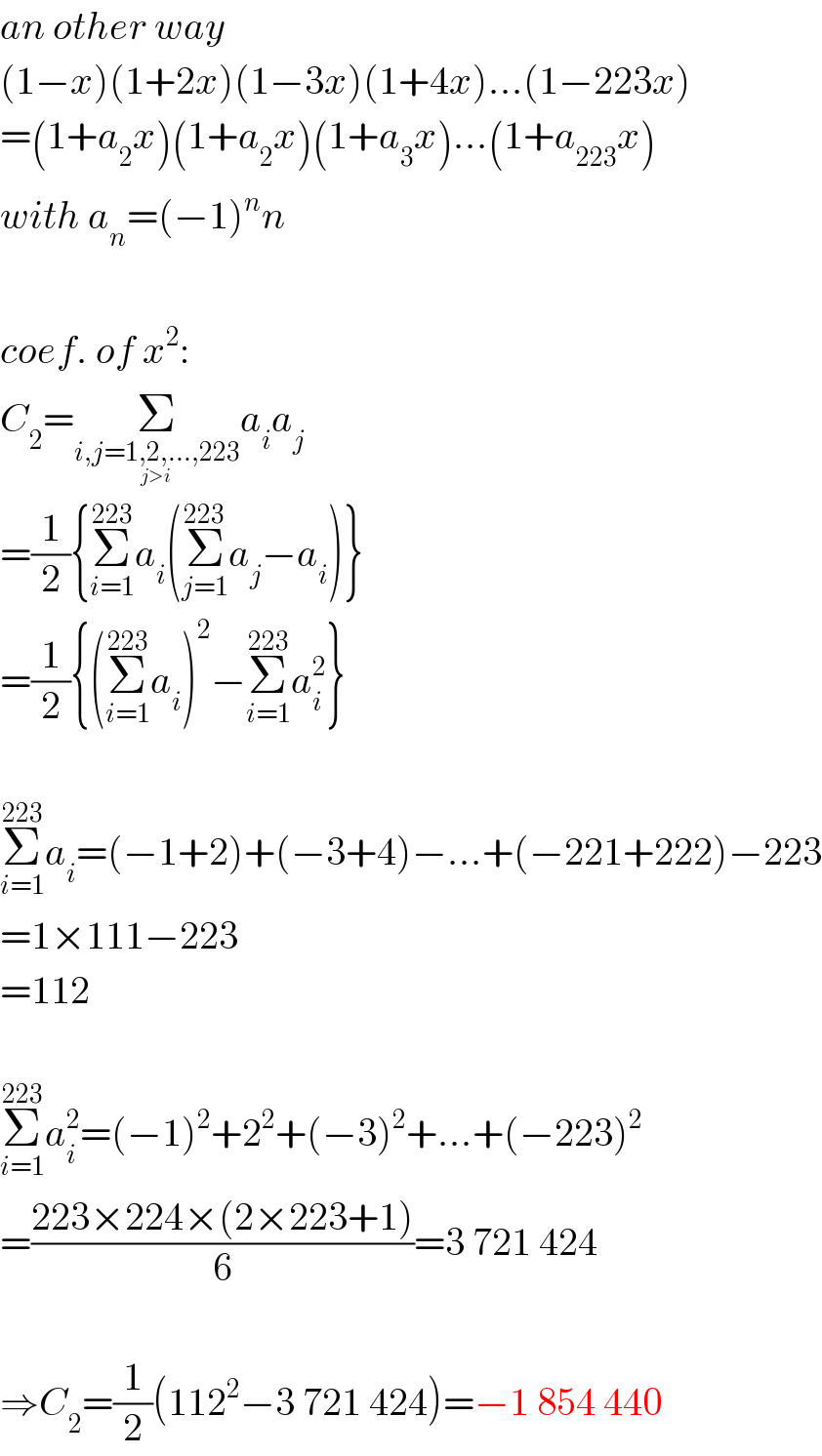
an other way (1−x)(1+2x)(1−3x)(1+4x)...(1−223x) =(1+a_2 x)(1+a_2 x)(1+a_3 x)...(1+a_(223) x) with a_n =(−1)^n n coef. of x^2 : C_2 =Σ_(i,j=1,2,...,223_(j>i) ) a_i a_j =(1/2){Σ_(i=1) ^(223) a_i (Σ_(j=1) ^(223) a_j −a_i )} =(1/2){(Σ_(i=1) ^(223) a_i )^2 −Σ_(i=1) ^(223) a_i ^2 } Σ_(i=1) ^(223) a_i =(−1+2)+(−3+4)−...+(−221+222)−223 =1×111−223 =112 Σ_(i=1) ^(223) a_i ^2 =(−1)^2 +2^2 +(−3)^2 +...+(−223)^2 =((223×224×(2×223+1))/6)=3 721 424 ⇒C_2 =(1/2)(112^2 −3 721 424)=−1 854 440
$${an}\:{other}\:{way} \\ $$$$\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+\mathrm{2}{x}\right)\left(\mathrm{1}−\mathrm{3}{x}\right)\left(\mathrm{1}+\mathrm{4}{x}\right)…\left(\mathrm{1}−\mathrm{223}{x}\right) \\ $$$$=\left(\mathrm{1}+{a}_{\mathrm{2}} {x}\right)\left(\mathrm{1}+{a}_{\mathrm{2}} {x}\right)\left(\mathrm{1}+{a}_{\mathrm{3}} {x}\right)…\left(\mathrm{1}+{a}_{\mathrm{223}} {x}\right) \\ $$$${with}\:{a}_{{n}} =\left(−\mathrm{1}\right)^{{n}} {n} \\ $$$$ \\ $$$${coef}.\:{of}\:{x}^{\mathrm{2}} : \\ $$$${C}_{\mathrm{2}} =\underset{\underset{{j}>{i}} {{i},{j}=\mathrm{1},\mathrm{2},…,\mathrm{223}}} {\sum}{a}_{{i}} {a}_{{j}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\underset{{i}=\mathrm{1}} {\overset{\mathrm{223}} {\sum}}{a}_{{i}} \left(\underset{{j}=\mathrm{1}} {\overset{\mathrm{223}} {\sum}}{a}_{{j}} −{a}_{{i}} \right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\left(\underset{{i}=\mathrm{1}} {\overset{\mathrm{223}} {\sum}}{a}_{{i}} \right)^{\mathrm{2}} −\underset{{i}=\mathrm{1}} {\overset{\mathrm{223}} {\sum}}{a}_{{i}} ^{\mathrm{2}} \right\} \\ $$$$ \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\mathrm{223}} {\sum}}{a}_{{i}} =\left(−\mathrm{1}+\mathrm{2}\right)+\left(−\mathrm{3}+\mathrm{4}\right)−…+\left(−\mathrm{221}+\mathrm{222}\right)−\mathrm{223} \\ $$$$=\mathrm{1}×\mathrm{111}−\mathrm{223} \\ $$$$=\mathrm{112} \\ $$$$ \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\mathrm{223}} {\sum}}{a}_{{i}} ^{\mathrm{2}} =\left(−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\left(−\mathrm{3}\right)^{\mathrm{2}} +…+\left(−\mathrm{223}\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{223}×\mathrm{224}×\left(\mathrm{2}×\mathrm{223}+\mathrm{1}\right)}{\mathrm{6}}=\mathrm{3}\:\mathrm{721}\:\mathrm{424} \\ $$$$ \\ $$$$\Rightarrow{C}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{112}^{\mathrm{2}} −\mathrm{3}\:\mathrm{721}\:\mathrm{424}\right)=−\mathrm{1}\:\mathrm{854}\:\mathrm{440} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *