Menu Close

Question-85461

Tinku Tara 0 Comments
Pin




Question Number 85461 by oustmuchiya@gmail.com last updated on 22/Mar/20
Commented by jagoll last updated on 22/Mar/20
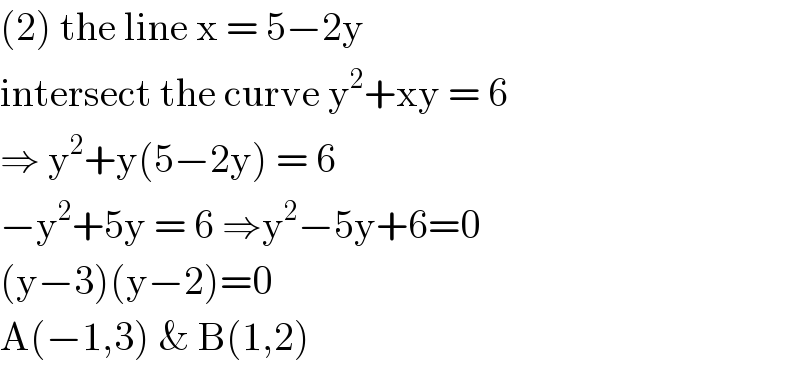
(2) the line x = 5−2y intersect the curve y^2 +xy = 6 ⇒ y^2 +y(5−2y) = 6 −y^2 +5y = 6 ⇒y^2 −5y+6=0 (y−3)(y−2)=0 A(−1,3) & B(1,2)
$$\left(\mathrm{2}\right)\:\mathrm{the}\:\mathrm{line}\:\mathrm{x}\:=\:\mathrm{5}−\mathrm{2y}\: \\ $$$$\mathrm{intersect}\:\mathrm{the}\:\mathrm{curve}\:\mathrm{y}^{\mathrm{2}} +\mathrm{xy}\:=\:\mathrm{6} \\ $$$$\Rightarrow\:\mathrm{y}^{\mathrm{2}} +\mathrm{y}\left(\mathrm{5}−\mathrm{2y}\right)\:=\:\mathrm{6} \\ $$$$−\mathrm{y}^{\mathrm{2}} +\mathrm{5y}\:=\:\mathrm{6}\:\Rightarrow\mathrm{y}^{\mathrm{2}} −\mathrm{5y}+\mathrm{6}=\mathrm{0} \\ $$$$\left(\mathrm{y}−\mathrm{3}\right)\left(\mathrm{y}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\mathrm{A}\left(−\mathrm{1},\mathrm{3}\right)\:\&\:\mathrm{B}\left(\mathrm{1},\mathrm{2}\right) \\ $$
Commented by jagoll last updated on 22/Mar/20
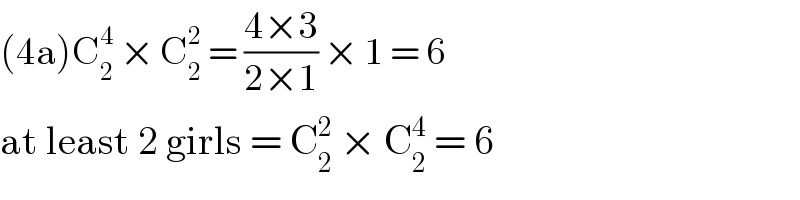
(4a)C_2 ^4 × C_2 ^2 = ((4×3)/(2×1)) × 1 = 6 at least 2 girls = C_2 ^2 × C_2 ^4 = 6
$$\left(\mathrm{4a}\right)\mathrm{C}_{\mathrm{2}} ^{\mathrm{4}} \:×\:\mathrm{C}_{\mathrm{2}} ^{\mathrm{2}} \:=\:\frac{\mathrm{4}×\mathrm{3}}{\mathrm{2}×\mathrm{1}}\:×\:\mathrm{1}\:=\:\mathrm{6} \\ $$$$\mathrm{at}\:\mathrm{least}\:\mathrm{2}\:\mathrm{girls}\:=\:\mathrm{C}_{\mathrm{2}} ^{\mathrm{2}} \:×\:\mathrm{C}_{\mathrm{2}} ^{\mathrm{4}} \:=\:\mathrm{6} \\ $$
Commented by jagoll last updated on 22/Mar/20
(4b)COMPUTER = 8!
$$\left(\mathrm{4b}\right)\mathrm{COMPUTER}\: \\ $$$$=\:\mathrm{8}!\: \\ $$
Commented by mathmax by abdo last updated on 22/Mar/20
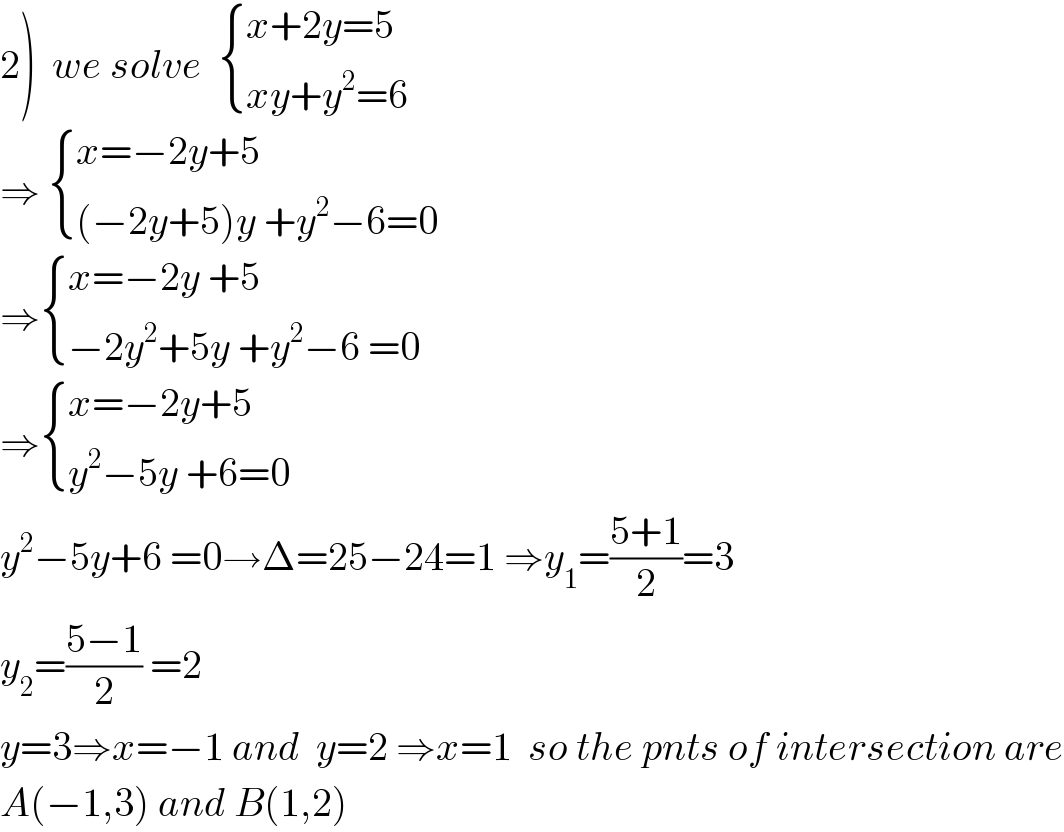
2) we solve { ((x+2y=5)),((xy+y^2 =6 )) :} ⇒ { ((x=−2y+5)),(((−2y+5)y +y^2 −6=0)) :} ⇒ { ((x=−2y +5)),((−2y^2 +5y +y^2 −6 =0)) :} ⇒ { ((x=−2y+5)),((y^2 −5y +6=0)) :} y^2 −5y+6 =0→Δ=25−24=1 ⇒y_1 =((5+1)/2)=3 y_2 =((5−1)/2) =2 y=3⇒x=−1 and y=2 ⇒x=1 so the pnts of intersection are A(−1,3) and B(1,2)
$$\left.\mathrm{2}\right)\:\:{we}\:{solve}\:\:\begin{cases}{{x}+\mathrm{2}{y}=\mathrm{5}}\\{{xy}+{y}^{\mathrm{2}} =\mathrm{6}\:}\end{cases} \\ $$$$\Rightarrow\:\begin{cases}{{x}=−\mathrm{2}{y}+\mathrm{5}}\\{\left(−\mathrm{2}{y}+\mathrm{5}\right){y}\:+{y}^{\mathrm{2}} −\mathrm{6}=\mathrm{0}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{{x}=−\mathrm{2}{y}\:+\mathrm{5}}\\{−\mathrm{2}{y}^{\mathrm{2}} +\mathrm{5}{y}\:+{y}^{\mathrm{2}} −\mathrm{6}\:=\mathrm{0}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{{x}=−\mathrm{2}{y}+\mathrm{5}}\\{{y}^{\mathrm{2}} −\mathrm{5}{y}\:+\mathrm{6}=\mathrm{0}}\end{cases} \\ $$$${y}^{\mathrm{2}} −\mathrm{5}{y}+\mathrm{6}\:=\mathrm{0}\rightarrow\Delta=\mathrm{25}−\mathrm{24}=\mathrm{1}\:\Rightarrow{y}_{\mathrm{1}} =\frac{\mathrm{5}+\mathrm{1}}{\mathrm{2}}=\mathrm{3} \\ $$$${y}_{\mathrm{2}} =\frac{\mathrm{5}−\mathrm{1}}{\mathrm{2}}\:=\mathrm{2} \\ $$$${y}=\mathrm{3}\Rightarrow{x}=−\mathrm{1}\:{and}\:\:{y}=\mathrm{2}\:\Rightarrow{x}=\mathrm{1}\:\:{so}\:{the}\:{pnts}\:{of}\:{intersection}\:{are} \\ $$$${A}\left(−\mathrm{1},\mathrm{3}\right)\:{and}\:{B}\left(\mathrm{1},\mathrm{2}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *