Question Number 85472 by liki last updated on 22/Mar/20

Commented by liki last updated on 22/Mar/20
$$\:…{please}\:{anyone}\:{help}\:{me}\:{now}… \\ $$
Commented by jagoll last updated on 22/Mar/20
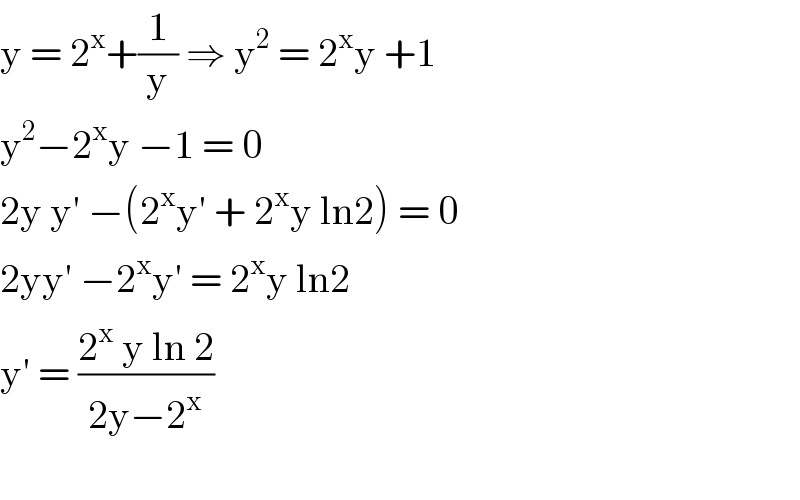
$$\mathrm{y}\:=\:\mathrm{2}^{\mathrm{x}} +\frac{\mathrm{1}}{\mathrm{y}}\:\Rightarrow\:\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{2}^{\mathrm{x}} \mathrm{y}\:+\mathrm{1} \\ $$$$\mathrm{y}^{\mathrm{2}} −\mathrm{2}^{\mathrm{x}} \mathrm{y}\:−\mathrm{1}\:=\:\mathrm{0} \\ $$$$\mathrm{2y}\:\mathrm{y}'\:−\left(\mathrm{2}^{\mathrm{x}} \mathrm{y}'\:+\:\mathrm{2}^{\mathrm{x}} \mathrm{y}\:\mathrm{ln2}\right)\:=\:\mathrm{0} \\ $$$$\mathrm{2yy}'\:−\mathrm{2}^{\mathrm{x}} \mathrm{y}'\:=\:\mathrm{2}^{\mathrm{x}} \mathrm{y}\:\mathrm{ln2} \\ $$$$\mathrm{y}'\:=\:\frac{\mathrm{2}^{\mathrm{x}} \:\mathrm{y}\:\mathrm{ln}\:\mathrm{2}}{\mathrm{2y}−\mathrm{2}^{\mathrm{x}} } \\ $$$$ \\ $$
Commented by jagoll last updated on 22/Mar/20

$$\mathrm{done} \\ $$
Commented by liki last updated on 22/Mar/20

$$…{Thank}\:{you}\:{sir}\:{be}\:{blessed} \\ $$
Answered by mind is power last updated on 22/Mar/20
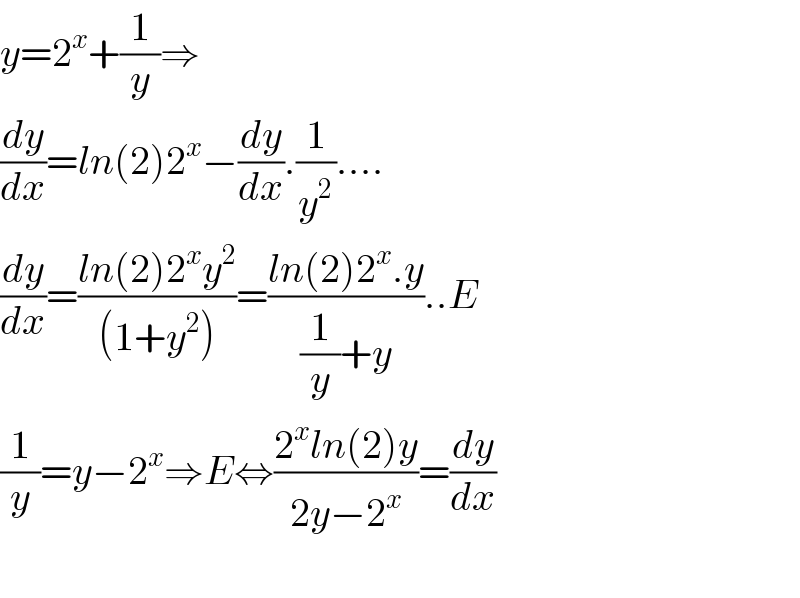
$${y}=\mathrm{2}^{{x}} +\frac{\mathrm{1}}{{y}}\Rightarrow \\ $$$$\frac{{dy}}{{dx}}={ln}\left(\mathrm{2}\right)\mathrm{2}^{{x}} −\frac{{dy}}{{dx}}.\frac{\mathrm{1}}{{y}^{\mathrm{2}} }…. \\ $$$$\frac{{dy}}{{dx}}=\frac{{ln}\left(\mathrm{2}\right)\mathrm{2}^{{x}} {y}^{\mathrm{2}} }{\left(\mathrm{1}+{y}^{\mathrm{2}} \right)}=\frac{{ln}\left(\mathrm{2}\right)\mathrm{2}^{{x}} .{y}}{\frac{\mathrm{1}}{{y}}+{y}}..{E} \\ $$$$\frac{\mathrm{1}}{{y}}={y}−\mathrm{2}^{{x}} \Rightarrow{E}\Leftrightarrow\frac{\mathrm{2}^{{x}} {ln}\left(\mathrm{2}\right){y}}{\mathrm{2}{y}−\mathrm{2}^{{x}} }=\frac{{dy}}{{dx}} \\ $$$$ \\ $$
Commented by liki last updated on 22/Mar/20
$$…{thanks}\:{alot}\:{sir}. \\ $$
Commented by mind is power last updated on 22/Mar/20

$${withe}\:{Pleasur} \\ $$
