Question-85606

Question Number 85606 by Rio Michael last updated on 23/Mar/20

Commented by Rio Michael last updated on 23/Mar/20

given that three weights W_1 , W_2 and 5N are suspended as shown above. A light inextensible string passing over smooth fixed pulleys makes angles 40° and 60° with the vertical and all the stings are taunt at point A. calculate the weights W_1 and W_2 .

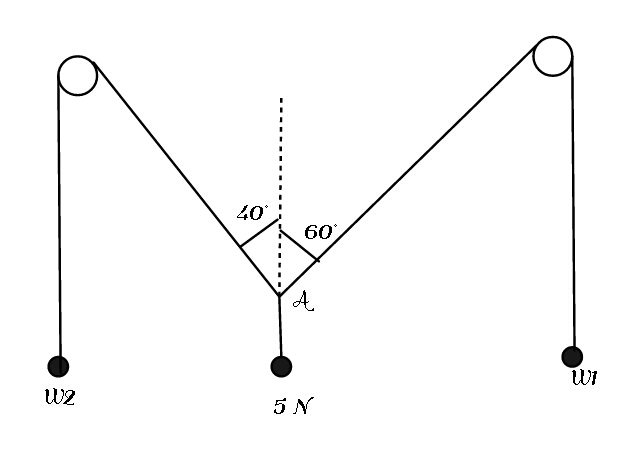
$$\mathrm{given}\:\mathrm{that}\:\mathrm{three}\:\mathrm{weights}\:\mathrm{W}_{\mathrm{1}} ,\:\mathrm{W}_{\mathrm{2}} \:{and}\:\mathrm{5}{N}\:\mathrm{are}\:\mathrm{suspended}\:\mathrm{as}\:\mathrm{shown}\:\mathrm{above}. \\ $$$$\mathrm{A}\:\mathrm{light}\:\mathrm{inextensible}\:\mathrm{string}\:\mathrm{passing}\:\mathrm{over}\:\mathrm{smooth}\:\mathrm{fixed}\:\mathrm{pulleys}\:\:\mathrm{makes}\:\mathrm{angles} \\ $$$$\mathrm{40}°\:\mathrm{and}\:\mathrm{60}°\:\mathrm{with}\:\mathrm{the}\:\mathrm{vertical}\:\mathrm{and}\:\mathrm{all}\:\mathrm{the}\:\mathrm{stings}\:\mathrm{are}\:\mathrm{taunt}\:\mathrm{at}\:\mathrm{point}\:\mathrm{A}. \\ $$$$\mathrm{calculate}\:\mathrm{the}\:\mathrm{weights}\:\mathrm{W}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{W}_{\mathrm{2}} . \\ $$

Commented by mr W last updated on 23/Mar/20

(W_1 /(sin 40°))=(W_2 /(sin 60°))=(G/(sin 100°)) G=5 N W_1 =((5 sin 40°)/(sin 100°))=3.26 N W_2 =((5 sin 60°)/(sin 100°))=4.40 N

$$\frac{{W}_{\mathrm{1}} }{\mathrm{sin}\:\mathrm{40}°}=\frac{{W}_{\mathrm{2}} }{\mathrm{sin}\:\mathrm{60}°}=\frac{{G}}{\mathrm{sin}\:\mathrm{100}°} \\ $$$${G}=\mathrm{5}\:{N} \\ $$$${W}_{\mathrm{1}} =\frac{\mathrm{5}\:\mathrm{sin}\:\mathrm{40}°}{\mathrm{sin}\:\mathrm{100}°}=\mathrm{3}.\mathrm{26}\:{N} \\ $$$${W}_{\mathrm{2}} =\frac{\mathrm{5}\:\mathrm{sin}\:\mathrm{60}°}{\mathrm{sin}\:\mathrm{100}°}=\mathrm{4}.\mathrm{40}\:{N} \\ $$

Commented by Rio Michael last updated on 23/Mar/20

thanks sir, but how did you get to using the sine rule that′s where don′t understand.

$$\mathrm{thanks}\:\mathrm{sir},\:\mathrm{but}\:\mathrm{how}\:\mathrm{did}\:\mathrm{you} \\ $$$$\mathrm{get}\:\mathrm{to}\:\mathrm{using}\:\mathrm{the}\:\mathrm{sine}\:\mathrm{rule}\:\mathrm{that}'\mathrm{s} \\ $$$$\mathrm{where}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}. \\ $$

Commented by mr W last updated on 23/Mar/20

$$\:\overset{\rightarrow} {\boldsymbol{{W}}_{\mathrm{2}} }+\overset{\rightarrow} {\boldsymbol{{W}}_{\mathrm{1}} }+\overset{\rightarrow} {\boldsymbol{{G}}}=\mathrm{0} \\ $$

Commented by mr W last updated on 23/Mar/20

Commented by Rio Michael last updated on 23/Mar/20

$$\mathrm{thanks}\:\mathrm{sir} \\ $$$$ \\ $$

Commented by john santu last updated on 25/Mar/20

(w_1 /(sin 140^o )) = (5/(sin 100^o )) ⇒ w_1 = ((5sin 140^o )/(sin 100^o )) (w_2 /(sin 120^o )) = (5/(sin 100^o )) ⇒w_2 = ((5sin 120^o )/(sin 100^o ))

$$\frac{{w}_{\mathrm{1}} }{\mathrm{sin}\:\mathrm{140}^{{o}} }\:=\:\frac{\mathrm{5}}{\mathrm{sin}\:\mathrm{100}^{{o}} }\:\Rightarrow\:{w}_{\mathrm{1}} \:=\:\frac{\mathrm{5sin}\:\mathrm{140}^{{o}} }{\mathrm{sin}\:\mathrm{100}^{{o}} } \\ $$$$\frac{{w}_{\mathrm{2}} }{\mathrm{sin}\:\mathrm{120}^{{o}} }\:=\:\frac{\mathrm{5}}{\mathrm{sin}\:\mathrm{100}^{{o}} }\:\Rightarrow{w}_{\mathrm{2}} \:=\:\frac{\mathrm{5sin}\:\mathrm{120}^{{o}} }{\mathrm{sin}\:\mathrm{100}^{{o}} } \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply