Question Number 85756 by TawaTawa1 last updated on 24/Mar/20
Commented by TawaTawa1 last updated on 24/Mar/20
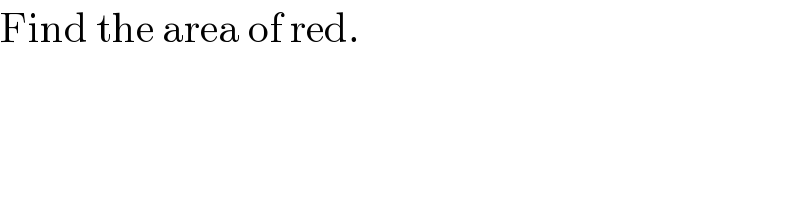
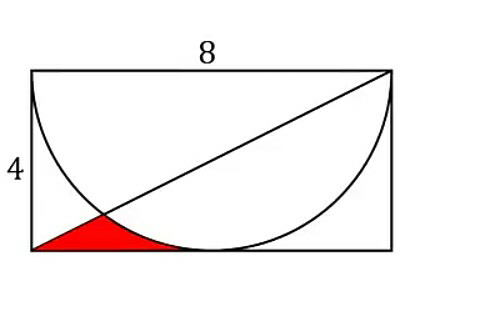
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{red}. \\ $$
Commented by Tony Lin last updated on 24/Mar/20
Commented by Tony Lin last updated on 24/Mar/20
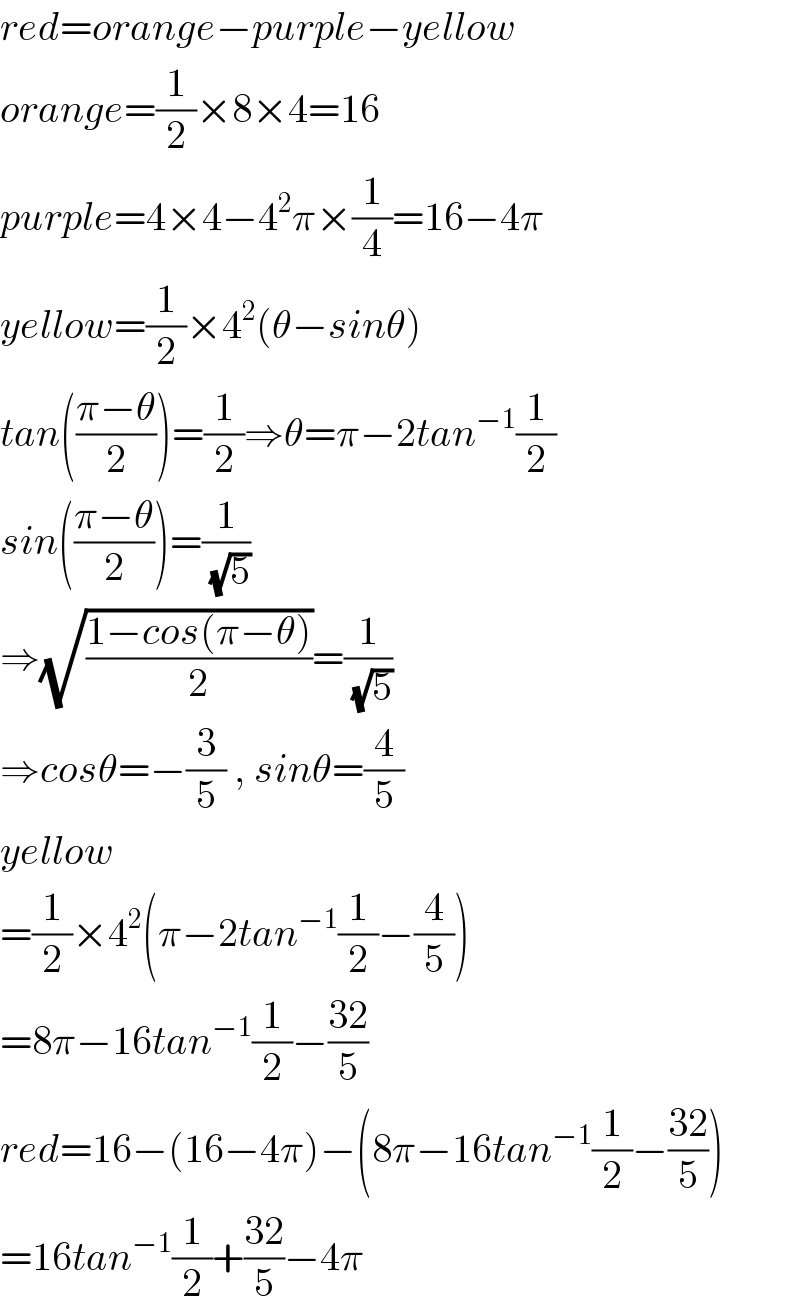
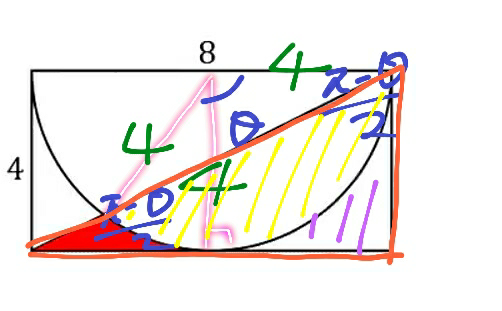
$${red}={orange}−{purple}−{yellow} \\ $$$${orange}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{8}×\mathrm{4}=\mathrm{16} \\ $$$${purple}=\mathrm{4}×\mathrm{4}−\mathrm{4}^{\mathrm{2}} \pi×\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{16}−\mathrm{4}\pi \\ $$$${yellow}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{4}^{\mathrm{2}} \left(\theta−{sin}\theta\right) \\ $$$${tan}\left(\frac{\pi−\theta}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\theta=\pi−\mathrm{2}{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}} \\ $$$${sin}\left(\frac{\pi−\theta}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$$\Rightarrow\sqrt{\frac{\mathrm{1}−{cos}\left(\pi−\theta\right)}{\mathrm{2}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$$\Rightarrow{cos}\theta=−\frac{\mathrm{3}}{\mathrm{5}}\:,\:{sin}\theta=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$${yellow} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{4}^{\mathrm{2}} \left(\pi−\mathrm{2}{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{4}}{\mathrm{5}}\right) \\ $$$$=\mathrm{8}\pi−\mathrm{16}{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{32}}{\mathrm{5}} \\ $$$${red}=\mathrm{16}−\left(\mathrm{16}−\mathrm{4}\pi\right)−\left(\mathrm{8}\pi−\mathrm{16}{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{32}}{\mathrm{5}}\right) \\ $$$$=\mathrm{16}{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{32}}{\mathrm{5}}−\mathrm{4}\pi \\ $$
Commented by TawaTawa1 last updated on 24/Mar/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by TawaTawa1 last updated on 26/Mar/20

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{it}. \\ $$
