Question-85762

Question Number 85762 by Power last updated on 24/Mar/20

Commented by MJS last updated on 24/Mar/20

$$\approx\mathrm{1}.\mathrm{43312742672} \\ $$

Commented by I want to learn more last updated on 24/Mar/20

If x = ⌈1, 2, 3, 4, 5⌉ ∴ x = 1 + (1/(2 + (1/(3 + (1/(4 + (1/(5 + x)))))))) ∴ x = 1 + (1/(2 + (1/(3 + ((5 + x)/(21 + 4x)))))) ∴ x = 1 + (1/(2 + (1/((63 + 12x + 5 + x)/(21 + 4x))))) ∴ x = 1 + (1/(2 + ((21 + 4x)/(68 + 13x)))) ∴ x = 1 + (1/((136 + 26x + 21 + 4x)/(68 + 13x))) ∴ x = 1 + ((68 + 13x)/(157 + 30x)) ∴ x = ((157 + 30x + 68 + 13x)/(157 + 30x)) ∴ x = ((225 + 43x)/(157 + 30x)) ∴ 30x^2 + 157x = 225 + 43x ∴ 30x^2 + 114x − 225 = 0 a = 30, b = 114, c = − 225 ∴ x = ≈ 1.433166662

$$\boldsymbol{\mathrm{If}}\:\:\:\boldsymbol{\mathrm{x}}\:\:\:=\:\:\:\lceil\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4},\:\mathrm{5}\rceil \\ $$$$\therefore\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}\:\:\:=\:\:\:\mathrm{1}\:\:+\:\:\frac{\mathrm{1}}{\mathrm{2}\:\:+\:\:\frac{\mathrm{1}}{\mathrm{3}\:\:+\:\:\frac{\mathrm{1}}{\mathrm{4}\:\:+\:\:\frac{\mathrm{1}}{\mathrm{5}\:\:+\:\boldsymbol{\mathrm{x}}}}}} \\ $$$$\therefore\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}\:\:\:=\:\:\:\mathrm{1}\:\:+\:\:\frac{\mathrm{1}}{\mathrm{2}\:\:+\:\:\frac{\mathrm{1}}{\mathrm{3}\:\:+\:\:\frac{\mathrm{5}\:\:+\:\:\boldsymbol{\mathrm{x}}}{\mathrm{21}\:+\:\mathrm{4}\boldsymbol{\mathrm{x}}}}} \\ $$$$\therefore\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}\:\:\:=\:\:\:\mathrm{1}\:\:+\:\:\frac{\mathrm{1}}{\mathrm{2}\:\:+\:\:\frac{\mathrm{1}}{\frac{\mathrm{63}\:+\:\mathrm{12}\boldsymbol{\mathrm{x}}\:+\:\mathrm{5}\:+\:\boldsymbol{\mathrm{x}}}{\mathrm{21}\:+\:\mathrm{4}\boldsymbol{\mathrm{x}}}}} \\ $$$$\therefore\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}\:\:\:=\:\:\:\mathrm{1}\:\:+\:\:\frac{\mathrm{1}}{\mathrm{2}\:\:+\:\:\frac{\mathrm{21}\:+\:\mathrm{4}\boldsymbol{\mathrm{x}}}{\mathrm{68}\:+\:\mathrm{13}\boldsymbol{\mathrm{x}}}} \\ $$$$\therefore\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}\:\:\:=\:\:\:\mathrm{1}\:\:+\:\:\frac{\mathrm{1}}{\frac{\mathrm{136}\:+\:\mathrm{26}\boldsymbol{\mathrm{x}}\:+\:\mathrm{21}\:+\:\mathrm{4}\boldsymbol{\mathrm{x}}}{\mathrm{68}\:+\:\mathrm{13}\boldsymbol{\mathrm{x}}}} \\ $$$$\therefore\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}\:\:\:=\:\:\:\mathrm{1}\:\:+\:\:\frac{\mathrm{68}\:+\:\mathrm{13}\boldsymbol{\mathrm{x}}}{\mathrm{157}\:+\:\mathrm{30}\boldsymbol{\mathrm{x}}} \\ $$$$\therefore\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}\:\:\:=\:\:\:\frac{\mathrm{157}\:\:+\:\:\mathrm{30}\boldsymbol{\mathrm{x}}\:\:+\:\:\mathrm{68}\:\:+\:\:\mathrm{13}\boldsymbol{\mathrm{x}}}{\mathrm{157}\:\:+\:\:\mathrm{30}\boldsymbol{\mathrm{x}}} \\ $$$$\therefore\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}\:\:\:=\:\:\:\frac{\mathrm{225}\:\:+\:\:\mathrm{43}\boldsymbol{\mathrm{x}}}{\mathrm{157}\:\:+\:\:\mathrm{30}\boldsymbol{\mathrm{x}}} \\ $$$$\therefore\:\:\:\:\:\:\:\:\:\:\mathrm{30}\boldsymbol{\mathrm{x}}^{\mathrm{2}} \:\:+\:\:\mathrm{157}\boldsymbol{\mathrm{x}}\:\:\:=\:\:\mathrm{225}\:\:+\:\:\mathrm{43}\boldsymbol{\mathrm{x}} \\ $$$$\therefore\:\:\:\:\:\:\:\:\:\:\mathrm{30}\boldsymbol{\mathrm{x}}^{\mathrm{2}} \:\:+\:\:\mathrm{114}\boldsymbol{\mathrm{x}}\:\:−\:\mathrm{225}\:\:=\:\:\mathrm{0} \\ $$$$\boldsymbol{\mathrm{a}}\:\:=\:\:\mathrm{30},\:\:\:\boldsymbol{\mathrm{b}}\:\:=\:\:\mathrm{114},\:\:\:\boldsymbol{\mathrm{c}}\:\:=\:\:−\:\mathrm{225} \\ $$$$\therefore\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}\:\:\:=\:\:\:\approx\:\:\mathrm{1}.\mathrm{433166662}\: \\ $$

Commented by Power last updated on 24/Mar/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\: \\ $$

Commented by MJS last updated on 24/Mar/20

but the question includes “...”, which means to infinity. you simply ignored this.

$$\mathrm{but}\:\mathrm{the}\:\mathrm{question}\:\mathrm{includes}\:“…'',\:\mathrm{which}\:\mathrm{means} \\ $$$$\mathrm{to}\:\mathrm{infinity}.\:\mathrm{you}\:\mathrm{simply}\:\mathrm{ignored}\:\mathrm{this}. \\ $$

Commented by I want to learn more last updated on 24/Mar/20

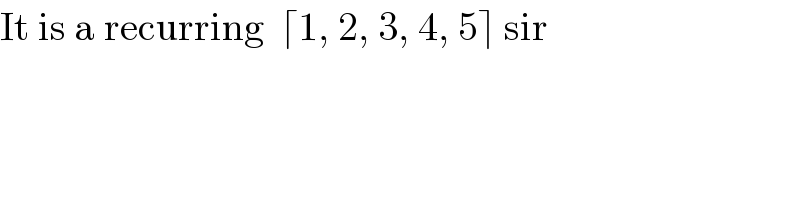
$$\mathrm{It}\:\mathrm{is}\:\mathrm{a}\:\mathrm{recurring}\:\:\lceil\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4},\:\mathrm{5}\rceil\:\mathrm{sir} \\ $$

Commented by I want to learn more last updated on 24/Mar/20

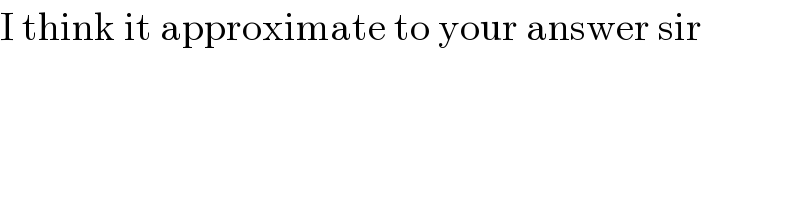
I think it approximate to your answer sir

$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{approximate}\:\mathrm{to}\:\mathrm{your}\:\mathrm{answer}\:\mathrm{sir} \\ $$

Commented by MJS last updated on 24/Mar/20

I think it′s [1,2,3,4,5,6,...] my value is an approximation of this

$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}'\mathrm{s}\:\left[\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{6},…\right] \\ $$$$\mathrm{my}\:\mathrm{value}\:\mathrm{is}\:\mathrm{an}\:\mathrm{approximation}\:\mathrm{of}\:\mathrm{this} \\ $$

Commented by I want to learn more last updated on 24/Mar/20

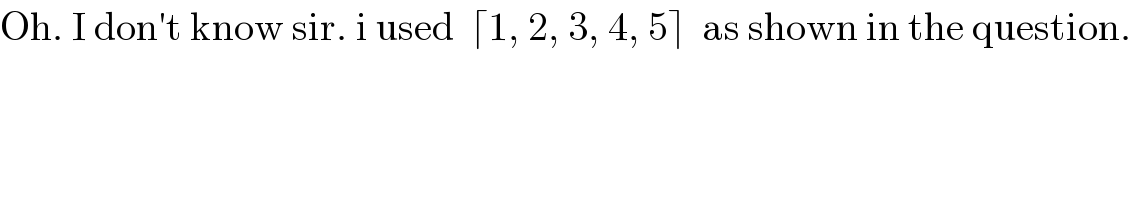
Oh. I don′t know sir. i used ⌈1, 2, 3, 4, 5⌉ as shown in the question.

$$\mathrm{Oh}.\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{used}\:\:\lceil\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4},\:\mathrm{5}\rceil\:\:\mathrm{as}\:\mathrm{shown}\:\mathrm{in}\:\mathrm{the}\:\mathrm{question}. \\ $$

Commented by MJS last updated on 24/Mar/20

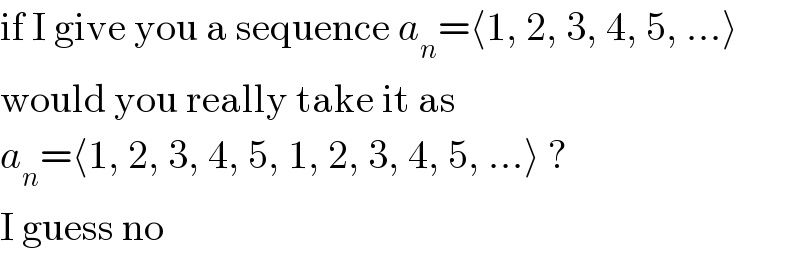
if I give you a sequence a_n =⟨1, 2, 3, 4, 5, ...⟩ would you really take it as a_n =⟨1, 2, 3, 4, 5, 1, 2, 3, 4, 5, ...⟩ ? I guess no

$$\mathrm{if}\:\mathrm{I}\:\mathrm{give}\:\mathrm{you}\:\mathrm{a}\:\mathrm{sequence}\:{a}_{{n}} =\langle\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4},\:\mathrm{5},\:…\rangle \\ $$$$\mathrm{would}\:\mathrm{you}\:\mathrm{really}\:\mathrm{take}\:\mathrm{it}\:\mathrm{as} \\ $$$${a}_{{n}} =\langle\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4},\:\mathrm{5},\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4},\:\mathrm{5},\:…\rangle\:? \\ $$$$\mathrm{I}\:\mathrm{guess}\:\mathrm{no} \\ $$

Commented by I want to learn more last updated on 24/Mar/20

That is infinite continue fraction sir. It is assume that the sequence repeat in that manner. As the dot dot dot ...

$$\mathrm{That}\:\mathrm{is}\:\mathrm{infinite}\:\mathrm{continue}\:\mathrm{fraction}\:\mathrm{sir}. \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{assume}\:\mathrm{that}\:\mathrm{the}\:\mathrm{sequence}\:\mathrm{repeat}\:\mathrm{in}\:\mathrm{that}\:\mathrm{manner}. \\ $$$$\mathrm{As}\:\mathrm{the}\:\mathrm{dot}\:\mathrm{dot}\:\mathrm{dot}\:… \\ $$

Commented by MJS last updated on 24/Mar/20

this is just your interpretation x=2+(1/(1+(1/(2+(1/(1+(1/(1+(1/(4+(1/(1+(1/(1+(1/(6+(1/(1+...)))))))))))))))))) x=e if we continue 2+[1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, ...] if I want a repetition I must show the first repeated number(s) like this: 2+[1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 2, ...]

$$\mathrm{this}\:\mathrm{is}\:\mathrm{just}\:\mathrm{your}\:\mathrm{interpretation} \\ $$$${x}=\mathrm{2}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{6}+\frac{\mathrm{1}}{\mathrm{1}+…}}}}}}}}} \\ $$$${x}=\mathrm{e}\:\mathrm{if}\:\mathrm{we}\:\mathrm{continue} \\ $$$$\mathrm{2}+\left[\mathrm{1},\:\mathrm{2},\:\mathrm{1},\:\mathrm{1},\:\mathrm{4},\:\mathrm{1},\:\mathrm{1},\:\mathrm{6},\:\mathrm{1},\:\mathrm{1},\:\mathrm{8},\:…\right] \\ $$$$\mathrm{if}\:\mathrm{I}\:\mathrm{want}\:\mathrm{a}\:\mathrm{repetition}\:\mathrm{I}\:\mathrm{must}\:\mathrm{show}\:\mathrm{the}\:\mathrm{first} \\ $$$$\mathrm{repeated}\:\mathrm{number}\left(\mathrm{s}\right)\:\mathrm{like}\:\mathrm{this}: \\ $$$$\mathrm{2}+\left[\mathrm{1},\:\mathrm{2},\:\mathrm{1},\:\mathrm{1},\:\mathrm{4},\:\mathrm{1},\:\mathrm{1},\:\mathrm{6},\:\mathrm{1},\:\mathrm{1},\:\mathrm{2},\:…\right] \\ $$

Commented by I want to learn more last updated on 25/Mar/20

$$\mathrm{Ok}\:\mathrm{sir}.\:\mathrm{Thanks}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply