Menu Close

Question-87105

Tinku Tara 0 Comments
Pin




Question Number 87105 by Chi Mes Try last updated on 02/Apr/20
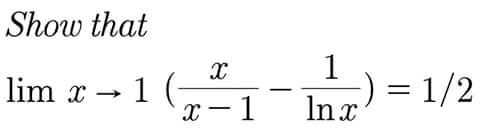
Commented by mathmax by abdo last updated on 03/Apr/20
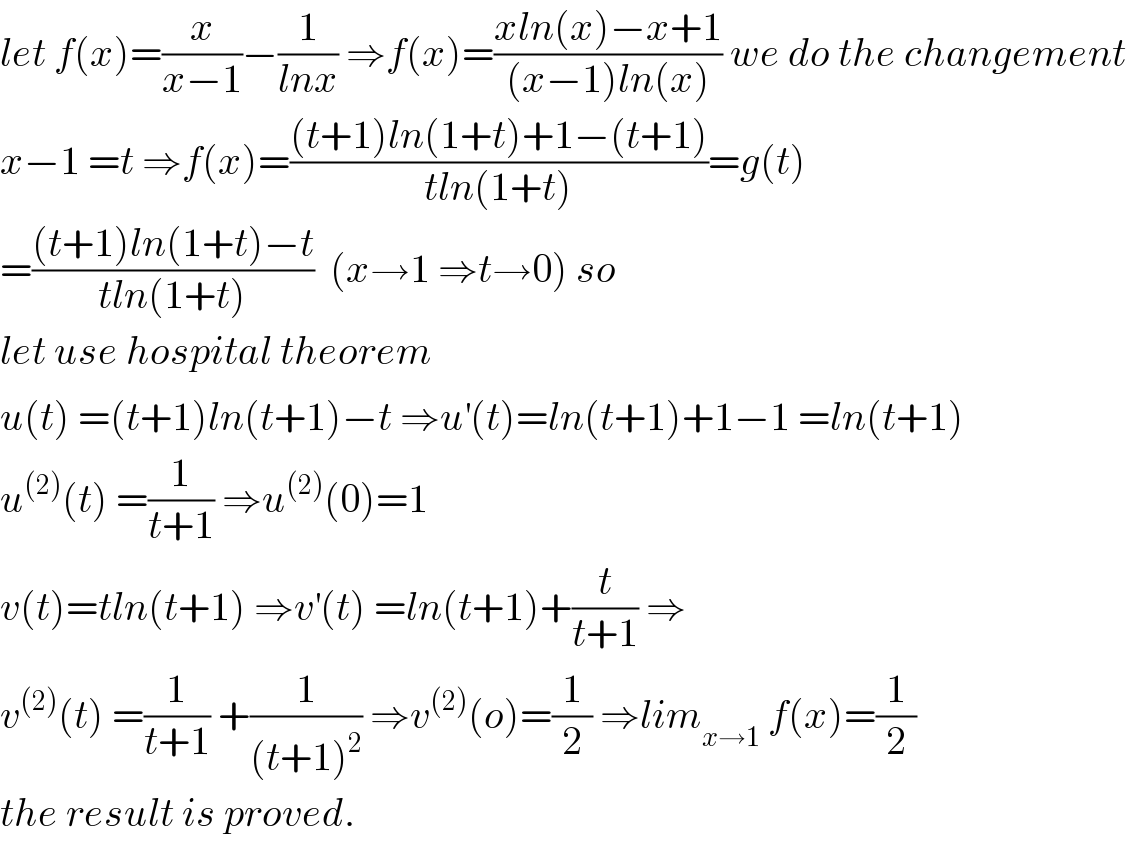
let f(x)=(x/(x−1))−(1/(lnx)) ⇒f(x)=((xln(x)−x+1)/((x−1)ln(x))) we do the changement x−1 =t ⇒f(x)=(((t+1)ln(1+t)+1−(t+1))/(tln(1+t)))=g(t) =(((t+1)ln(1+t)−t)/(tln(1+t))) (x→1 ⇒t→0) so let use hospital theorem u(t) =(t+1)ln(t+1)−t ⇒u^′ (t)=ln(t+1)+1−1 =ln(t+1) u^((2)) (t) =(1/(t+1)) ⇒u^((2)) (0)=1 v(t)=tln(t+1) ⇒v^′ (t) =ln(t+1)+(t/(t+1)) ⇒ v^((2)) (t) =(1/(t+1)) +(1/((t+1)^2 )) ⇒v^((2)) (o)=(1/2) ⇒lim_(x→1) f(x)=(1/2) the result is proved.
$${let}\:{f}\left({x}\right)=\frac{{x}}{{x}−\mathrm{1}}−\frac{\mathrm{1}}{{lnx}}\:\Rightarrow{f}\left({x}\right)=\frac{{xln}\left({x}\right)−{x}+\mathrm{1}}{\left({x}−\mathrm{1}\right){ln}\left({x}\right)}\:{we}\:{do}\:{the}\:{changement} \\ $$$${x}−\mathrm{1}\:={t}\:\Rightarrow{f}\left({x}\right)=\frac{\left({t}+\mathrm{1}\right){ln}\left(\mathrm{1}+{t}\right)+\mathrm{1}−\left({t}+\mathrm{1}\right)}{{tln}\left(\mathrm{1}+{t}\right)}={g}\left({t}\right) \\ $$$$=\frac{\left({t}+\mathrm{1}\right){ln}\left(\mathrm{1}+{t}\right)−{t}}{{tln}\left(\mathrm{1}+{t}\right)}\:\:\left({x}\rightarrow\mathrm{1}\:\Rightarrow{t}\rightarrow\mathrm{0}\right)\:{so} \\ $$$${let}\:{use}\:{hospital}\:{theorem} \\ $$$${u}\left({t}\right)\:=\left({t}+\mathrm{1}\right){ln}\left({t}+\mathrm{1}\right)−{t}\:\Rightarrow{u}^{'} \left({t}\right)={ln}\left({t}+\mathrm{1}\right)+\mathrm{1}−\mathrm{1}\:={ln}\left({t}+\mathrm{1}\right) \\ $$$${u}^{\left(\mathrm{2}\right)} \left({t}\right)\:=\frac{\mathrm{1}}{{t}+\mathrm{1}}\:\Rightarrow{u}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)=\mathrm{1} \\ $$$${v}\left({t}\right)={tln}\left({t}+\mathrm{1}\right)\:\Rightarrow{v}^{'} \left({t}\right)\:={ln}\left({t}+\mathrm{1}\right)+\frac{{t}}{{t}+\mathrm{1}}\:\Rightarrow \\ $$$${v}^{\left(\mathrm{2}\right)} \left({t}\right)\:=\frac{\mathrm{1}}{{t}+\mathrm{1}}\:+\frac{\mathrm{1}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow{v}^{\left(\mathrm{2}\right)} \left({o}\right)=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{1}} \:{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${the}\:{result}\:{is}\:{proved}. \\ $$
Answered by MJS last updated on 02/Apr/20
2×l′Hopital lim_(x→1) ((xln x −x+1)/((x−1)ln x)) = lim_(x→1) (((d^2 /dx^2 )[xln x −x+1])/((d^2 /dx^2 )[(x−1)ln x])) = =lim_(x→1) (x/(x+1)) =(1/2)
$$\mathrm{2}×\mathrm{l}'\mathrm{Hopital} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{x}\mathrm{ln}\:{x}\:−{x}+\mathrm{1}}{\left({x}−\mathrm{1}\right)\mathrm{ln}\:{x}}\:=\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }\left[{x}\mathrm{ln}\:{x}\:−{x}+\mathrm{1}\right]}{\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }\left[\left({x}−\mathrm{1}\right)\mathrm{ln}\:{x}\right]}\:= \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{x}}{{x}+\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by $@ty@m123 last updated on 03/Apr/20
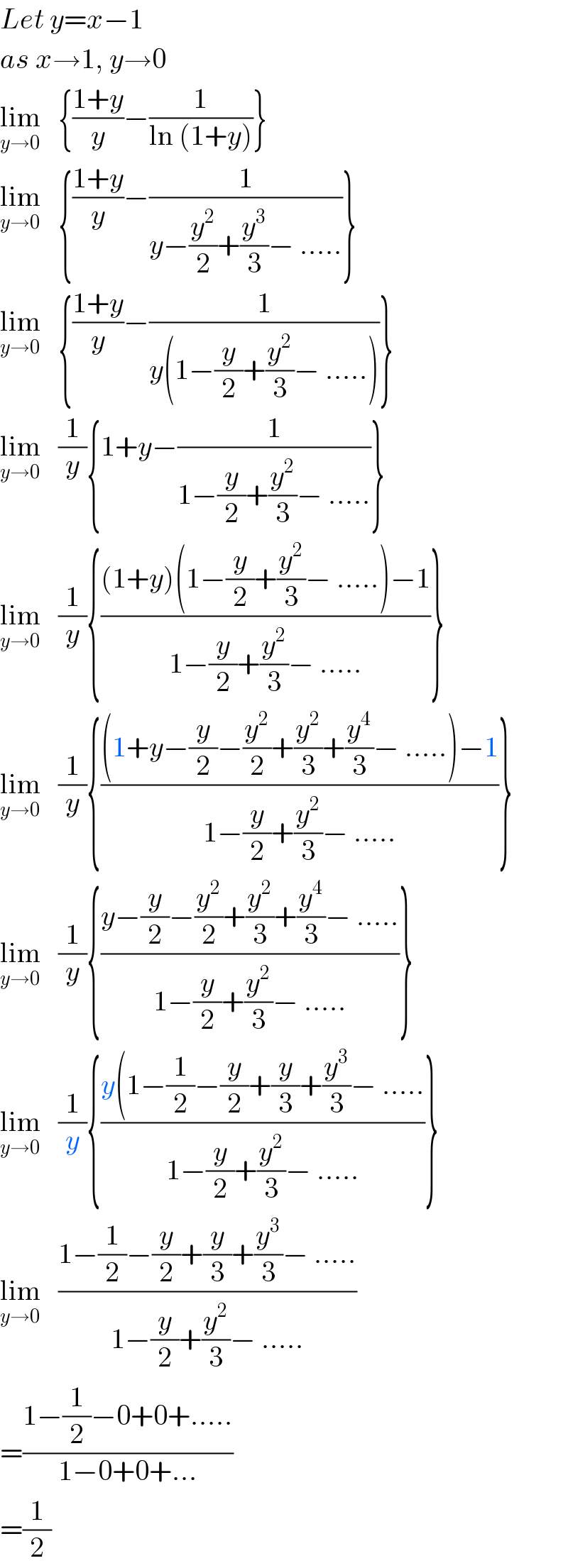
Let y=x−1 as x→1, y→0 lim_(y→0) {((1+y)/y)−(1/(ln (1+y)))} lim_(y→0) {((1+y)/y)−(1/(y−(y^2 /2)+(y^3 /3)− .....))} lim_(y→0) {((1+y)/y)−(1/(y(1−(y/2)+(y^2 /3)− .....)))} lim_(y→0) (1/y){1+y−(1/(1−(y/2)+(y^2 /3)− .....))} lim_(y→0) (1/y){(((1+y)(1−(y/2)+(y^2 /3)− .....)−1)/(1−(y/2)+(y^2 /3)− .....))} lim_(y→0) (1/y){(((1+y−(y/2)−(y^2 /2)+(y^2 /3)+(y^4 /3)− .....)−1)/(1−(y/2)+(y^2 /3)− .....))} lim_(y→0) (1/y){((y−(y/2)−(y^2 /2)+(y^2 /3)+(y^4 /3)− .....)/(1−(y/2)+(y^2 /3)− .....))} lim_(y→0) (1/y){((y(1−(1/2)−(y/2)+(y/3)+(y^3 /3)− .....)/(1−(y/2)+(y^2 /3)− .....))} lim_(y→0) ((1−(1/2)−(y/2)+(y/3)+(y^3 /3)− .....)/(1−(y/2)+(y^2 /3)− .....)) =((1−(1/2)−0+0+.....)/(1−0+0+...)) =(1/2)
$${Let}\:{y}={x}−\mathrm{1} \\ $$$${as}\:{x}\rightarrow\mathrm{1},\:{y}\rightarrow\mathrm{0} \\ $$$$\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\left\{\frac{\mathrm{1}+{y}}{{y}}−\frac{\mathrm{1}}{\mathrm{ln}\:\left(\mathrm{1}+{y}\right)}\right\} \\ $$$$\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\left\{\frac{\mathrm{1}+{y}}{{y}}−\frac{\mathrm{1}}{{y}−\frac{{y}^{\mathrm{2}} }{\mathrm{2}}+\frac{{y}^{\mathrm{3}} }{\mathrm{3}}−\:…..}\right\} \\ $$$$\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\left\{\frac{\mathrm{1}+{y}}{{y}}−\frac{\mathrm{1}}{{y}\left(\mathrm{1}−\frac{{y}}{\mathrm{2}}+\frac{{y}^{\mathrm{2}} }{\mathrm{3}}−\:…..\right)}\right\} \\ $$$$\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\frac{\mathrm{1}}{{y}}\left\{\mathrm{1}+{y}−\frac{\mathrm{1}}{\mathrm{1}−\frac{{y}}{\mathrm{2}}+\frac{{y}^{\mathrm{2}} }{\mathrm{3}}−\:…..}\right\} \\ $$$$\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\frac{\mathrm{1}}{{y}}\left\{\frac{\left(\mathrm{1}+{y}\right)\left(\mathrm{1}−\frac{{y}}{\mathrm{2}}+\frac{{y}^{\mathrm{2}} }{\mathrm{3}}−\:…..\right)−\mathrm{1}}{\mathrm{1}−\frac{{y}}{\mathrm{2}}+\frac{{y}^{\mathrm{2}} }{\mathrm{3}}−\:…..}\right\} \\ $$$$\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\frac{\mathrm{1}}{{y}}\left\{\frac{\left(\mathrm{1}+{y}−\frac{{y}}{\mathrm{2}}−\frac{{y}^{\mathrm{2}} }{\mathrm{2}}+\frac{{y}^{\mathrm{2}} }{\mathrm{3}}+\frac{{y}^{\mathrm{4}} }{\mathrm{3}}−\:…..\right)−\mathrm{1}}{\mathrm{1}−\frac{{y}}{\mathrm{2}}+\frac{{y}^{\mathrm{2}} }{\mathrm{3}}−\:…..}\right\} \\ $$$$\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\frac{\mathrm{1}}{{y}}\left\{\frac{{y}−\frac{{y}}{\mathrm{2}}−\frac{{y}^{\mathrm{2}} }{\mathrm{2}}+\frac{{y}^{\mathrm{2}} }{\mathrm{3}}+\frac{{y}^{\mathrm{4}} }{\mathrm{3}}−\:…..}{\mathrm{1}−\frac{{y}}{\mathrm{2}}+\frac{{y}^{\mathrm{2}} }{\mathrm{3}}−\:…..}\right\} \\ $$$$\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\frac{\mathrm{1}}{{y}}\left\{\frac{{y}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{{y}}{\mathrm{2}}+\frac{{y}}{\mathrm{3}}+\frac{{y}^{\mathrm{3}} }{\mathrm{3}}−\:…..\right.}{\mathrm{1}−\frac{{y}}{\mathrm{2}}+\frac{{y}^{\mathrm{2}} }{\mathrm{3}}−\:…..}\right\} \\ $$$$\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{{y}}{\mathrm{2}}+\frac{{y}}{\mathrm{3}}+\frac{{y}^{\mathrm{3}} }{\mathrm{3}}−\:…..}{\mathrm{1}−\frac{{y}}{\mathrm{2}}+\frac{{y}^{\mathrm{2}} }{\mathrm{3}}−\:…..} \\ $$$$=\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{0}+\mathrm{0}+…..}{\mathrm{1}−\mathrm{0}+\mathrm{0}+…} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *