Question Number 87125 by jagoll last updated on 03/Apr/20
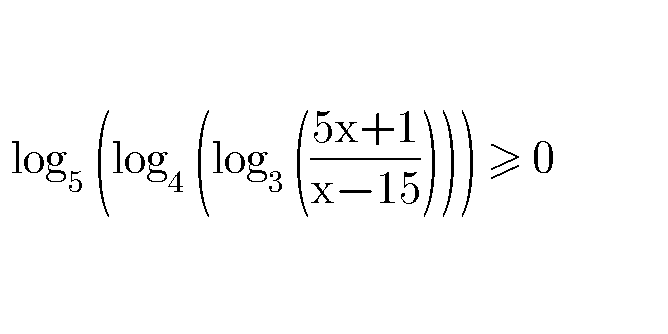
Commented by john santu last updated on 03/Apr/20

$$\mathrm{cooll} \\ $$
Commented by john santu last updated on 03/Apr/20
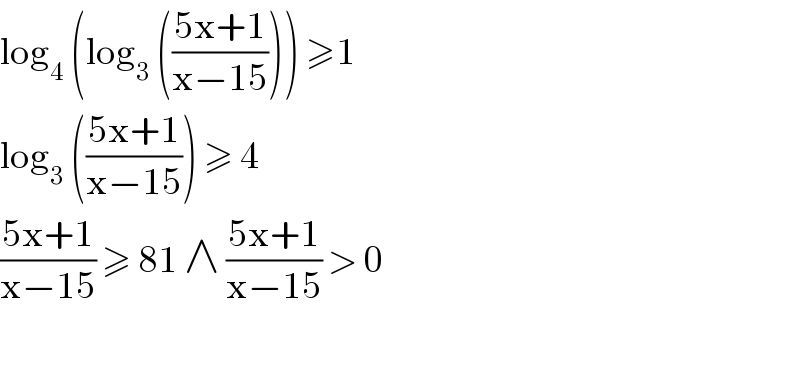
$$\mathrm{log}_{\mathrm{4}} \:\left(\mathrm{log}_{\mathrm{3}} \:\left(\frac{\mathrm{5x}+\mathrm{1}}{\mathrm{x}−\mathrm{15}}\right)\right)\:\geqslant\mathrm{1} \\ $$$$\mathrm{log}_{\mathrm{3}} \:\left(\frac{\mathrm{5x}+\mathrm{1}}{\mathrm{x}−\mathrm{15}}\right)\:\geqslant\:\mathrm{4}\: \\ $$$$\frac{\mathrm{5x}+\mathrm{1}}{\mathrm{x}−\mathrm{15}}\:\geqslant\:\mathrm{81}\:\wedge\:\frac{\mathrm{5x}+\mathrm{1}}{\mathrm{x}−\mathrm{15}}\:>\:\mathrm{0} \\ $$$$ \\ $$
Commented by MJS last updated on 03/Apr/20
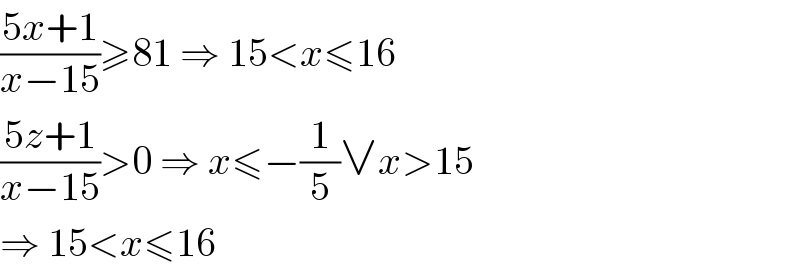
$$\frac{\mathrm{5}{x}+\mathrm{1}}{{x}−\mathrm{15}}\geqslant\mathrm{81}\:\Rightarrow\:\mathrm{15}<{x}\leqslant\mathrm{16} \\ $$$$\frac{\mathrm{5}{z}+\mathrm{1}}{{x}−\mathrm{15}}>\mathrm{0}\:\Rightarrow\:{x}\leqslant−\frac{\mathrm{1}}{\mathrm{5}}\vee{x}>\mathrm{15} \\ $$$$\Rightarrow\:\mathrm{15}<{x}\leqslant\mathrm{16} \\ $$
