Question Number 87285 by ajfour last updated on 03/Apr/20
Commented by ajfour last updated on 03/Apr/20
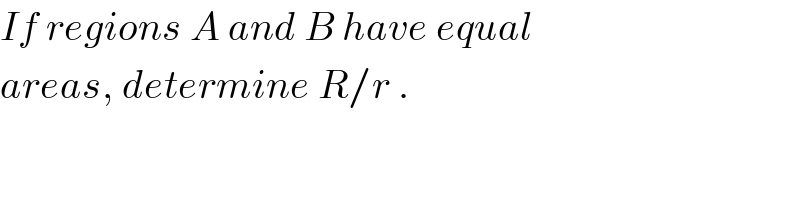
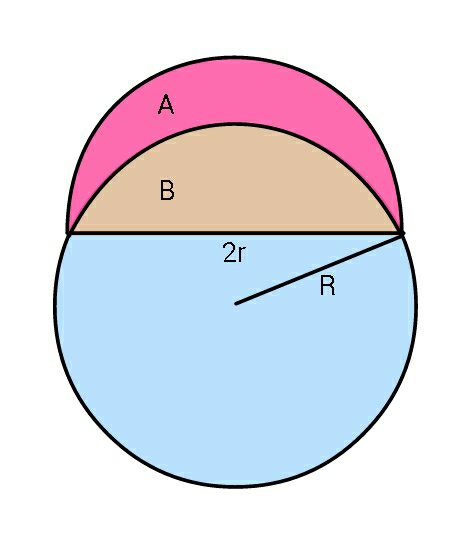
$${If}\:{regions}\:{A}\:{and}\:{B}\:{have}\:{equal} \\ $$$${areas},\:{determine}\:{R}/{r}\:. \\ $$
Answered by mr W last updated on 03/Apr/20
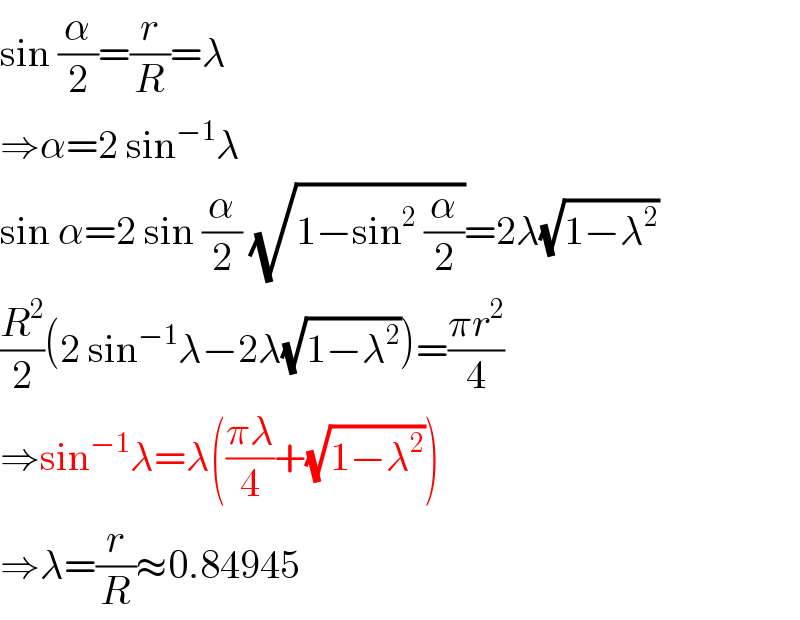
$$\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}=\frac{{r}}{{R}}=\lambda \\ $$$$\Rightarrow\alpha=\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \lambda \\ $$$$\mathrm{sin}\:\alpha=\mathrm{2}\:\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}\:\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}}=\mathrm{2}\lambda\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} } \\ $$$$\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \lambda−\mathrm{2}\lambda\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }\right)=\frac{\pi{r}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{sin}^{−\mathrm{1}} \lambda=\lambda\left(\frac{\pi\lambda}{\mathrm{4}}+\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }\right) \\ $$$$\Rightarrow\lambda=\frac{{r}}{{R}}\approx\mathrm{0}.\mathrm{84945} \\ $$
Commented by ajfour last updated on 03/Apr/20
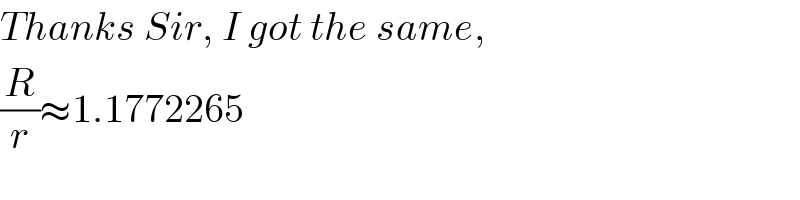
$${Thanks}\:{Sir},\:{I}\:{got}\:{the}\:{same}, \\ $$$$\frac{{R}}{{r}}\approx\mathrm{1}.\mathrm{1772265} \\ $$
Commented by Ar Brandon last updated on 03/Apr/20
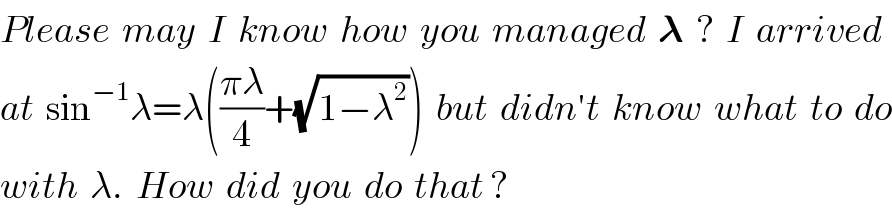
$${Please}\:\:{may}\:\:{I}\:\:{know}\:\:{how}\:\:{you}\:\:{managed}\:\:\boldsymbol{\lambda}\:\:?\:\:{I}\:\:{arrived} \\ $$$${at}\:\:\mathrm{sin}^{−\mathrm{1}} \lambda=\lambda\left(\frac{\pi\lambda}{\mathrm{4}}+\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }\right)\:\:{but}\:\:{didn}'{t}\:\:{know}\:\:{what}\:\:{to}\:\:{do} \\ $$$${with}\:\:\lambda.\:\:{How}\:\:{did}\:\:{you}\:\:{do}\:\:{that}\:? \\ $$
Commented by ajfour last updated on 03/Apr/20

$${calculator}\:{Sir}. \\ $$
Commented by mr W last updated on 03/Apr/20

$${it}\:{is}\:{not}\:{possible}\:{to}\:{solve}\:{the}\:{equation} \\ $$$${exactly}.\:{usually}\:{i}\:{use}\:{the}\:{app}\:{Grapher} \\ $$$${to}\:{get}\:{the}\:{approximation}. \\ $$
Commented by Ar Brandon last updated on 03/Apr/20
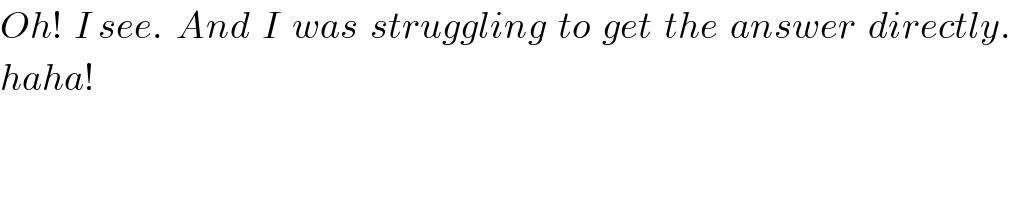
$${Oh}!\:\:{I}\:{see}.\:\:{And}\:\:{I}\:\:{was}\:\:{struggling}\:\:{to}\:\:{get}\:\:{the}\:\:{answer}\:\:{directly}. \\ $$$${haha}! \\ $$
