Question Number 87335 by naka3546 last updated on 04/Apr/20
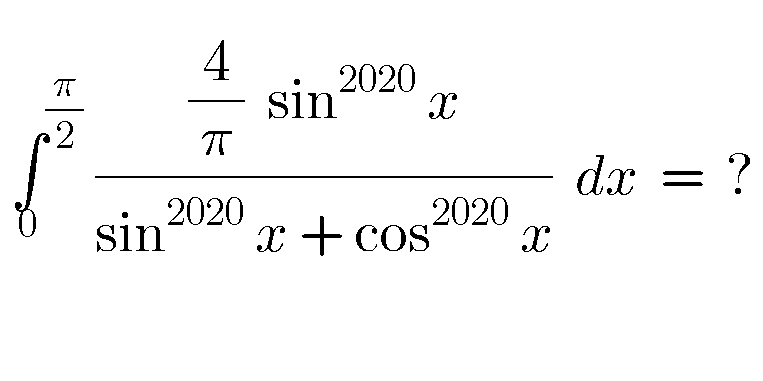
Answered by TANMAY PANACEA. last updated on 04/Apr/20
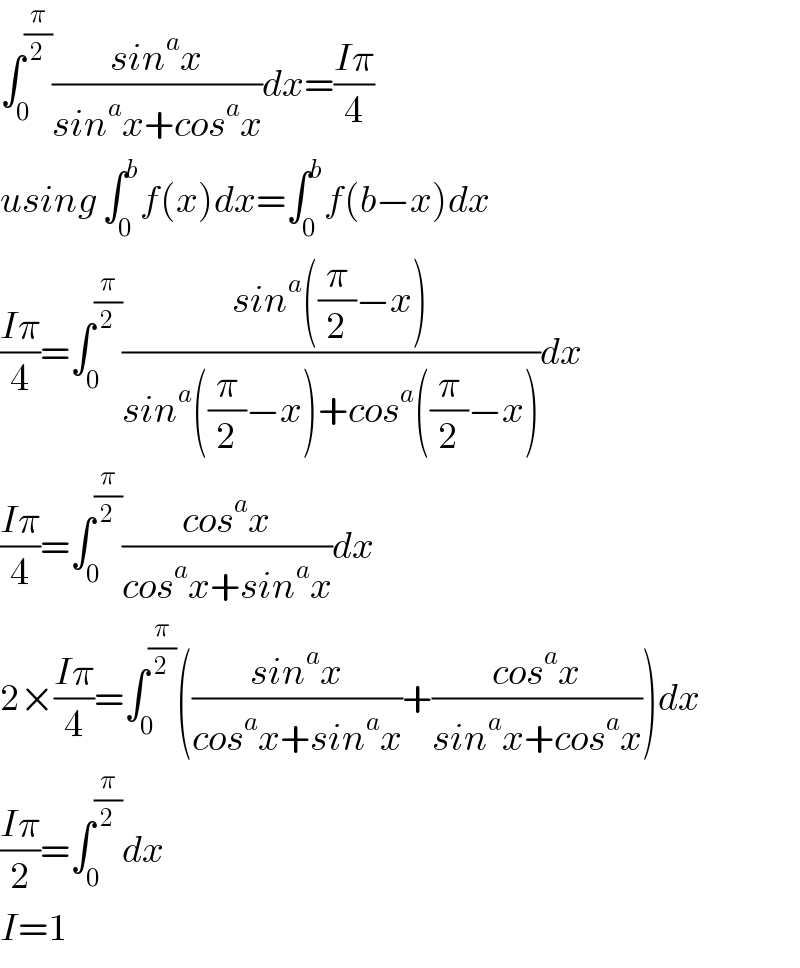
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}^{{a}} {x}}{{sin}^{{a}} {x}+{cos}^{{a}} {x}}{dx}=\frac{{I}\pi}{\mathrm{4}} \\ $$$${using}\:\int_{\mathrm{0}} ^{{b}} {f}\left({x}\right){dx}=\int_{\mathrm{0}} ^{{b}} {f}\left({b}−{x}\right){dx} \\ $$$$\frac{{I}\pi}{\mathrm{4}}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}^{{a}} \left(\frac{\pi}{\mathrm{2}}−{x}\right)}{{sin}^{{a}} \left(\frac{\pi}{\mathrm{2}}−{x}\right)+{cos}^{{a}} \left(\frac{\pi}{\mathrm{2}}−{x}\right)}{dx} \\ $$$$\frac{{I}\pi}{\mathrm{4}}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cos}^{{a}} {x}}{{cos}^{{a}} {x}+{sin}^{{a}} {x}}{dx} \\ $$$$\mathrm{2}×\frac{{I}\pi}{\mathrm{4}}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{{sin}^{{a}} {x}}{{cos}^{{a}} {x}+{sin}^{{a}} {x}}+\frac{{cos}^{{a}} {x}}{{sin}^{{a}} {x}+{cos}^{{a}} {x}}\right){dx} \\ $$$$\frac{{I}\pi}{\mathrm{2}}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {dx} \\ $$$${I}=\mathrm{1} \\ $$
