Question Number 87376 by naka3546 last updated on 04/Apr/20
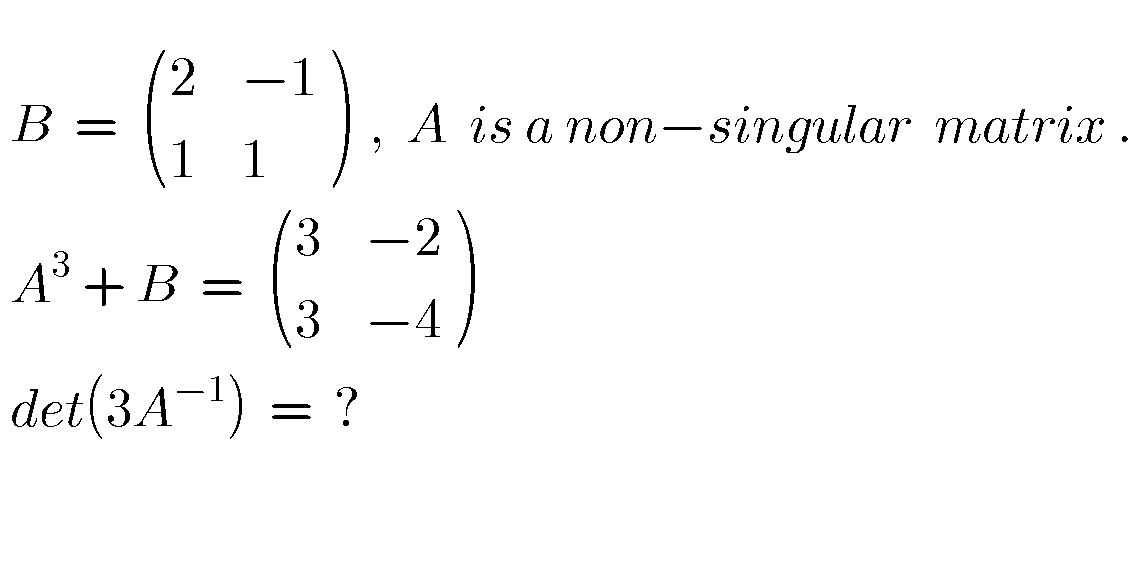
Answered by john santu last updated on 04/Apr/20
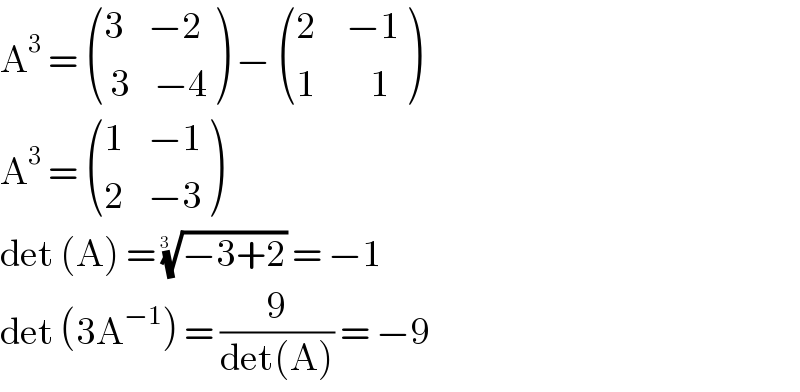
$$\mathrm{A}^{\mathrm{3}} \:=\:\begin{pmatrix}{\mathrm{3}\:\:\:\:−\mathrm{2}}\\{\:\mathrm{3}\:\:\:\:−\mathrm{4}}\end{pmatrix}\:−\:\begin{pmatrix}{\mathrm{2}\:\:\:\:\:−\mathrm{1}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$$\mathrm{A}^{\mathrm{3}} \:=\:\begin{pmatrix}{\mathrm{1}\:\:\:\:−\mathrm{1}}\\{\mathrm{2}\:\:\:\:−\mathrm{3}}\end{pmatrix} \\ $$$$\mathrm{det}\:\left(\mathrm{A}\right)\:=\:\sqrt[{\mathrm{3}\:\:}]{−\mathrm{3}+\mathrm{2}}\:=\:−\mathrm{1} \\ $$$$\mathrm{det}\:\left(\mathrm{3A}^{−\mathrm{1}} \right)\:=\:\frac{\mathrm{9}}{\mathrm{det}\left(\mathrm{A}\right)}\:=\:−\mathrm{9} \\ $$
