Question Number 87413 by ajfour last updated on 04/Apr/20
Commented by ajfour last updated on 04/Apr/20
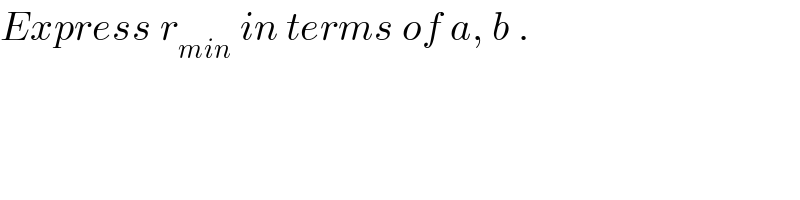
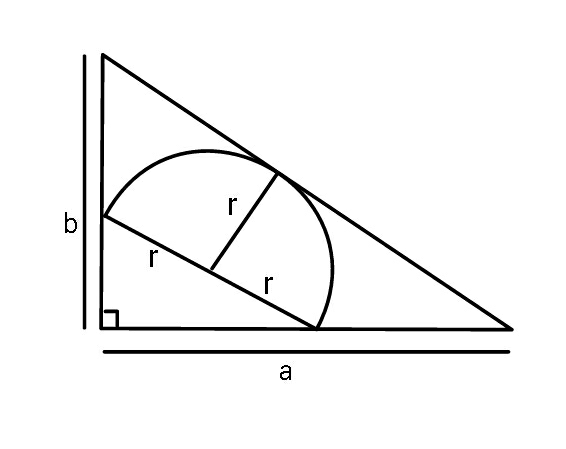
$${Express}\:{r}_{{min}} \:{in}\:{terms}\:{of}\:{a},\:{b}\:. \\ $$
Answered by mr W last updated on 04/Apr/20
Commented by mr W last updated on 04/Apr/20
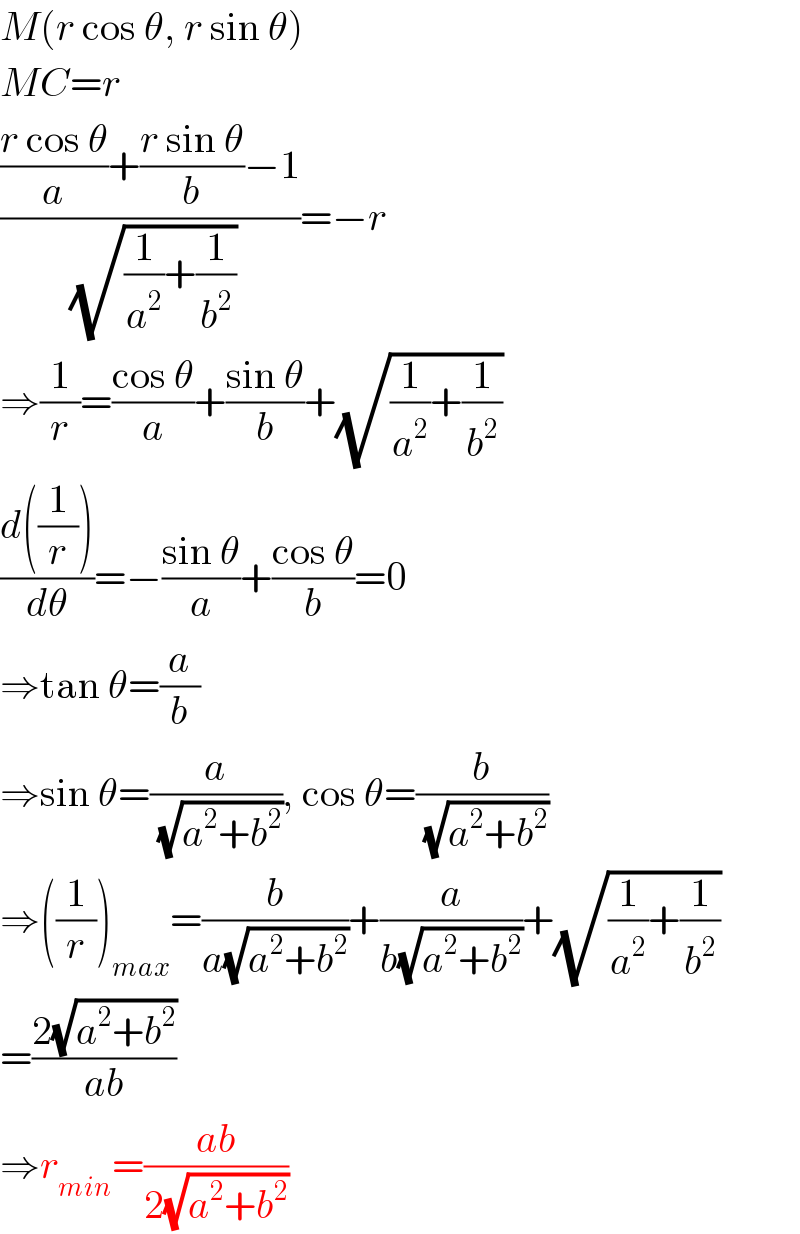
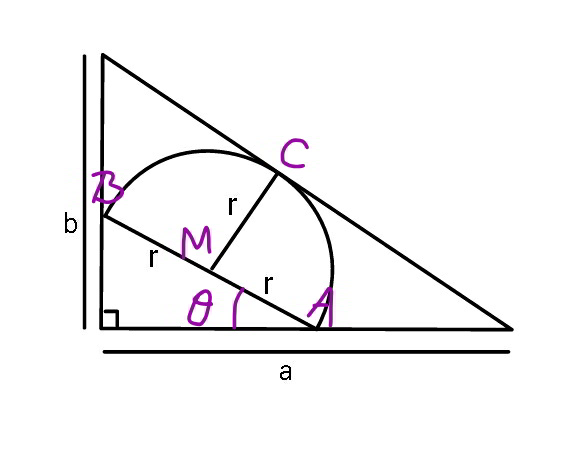
$${M}\left({r}\:\mathrm{cos}\:\theta,\:{r}\:\mathrm{sin}\:\theta\right) \\ $$$${MC}={r} \\ $$$$\frac{\frac{{r}\:\mathrm{cos}\:\theta}{{a}}+\frac{{r}\:\mathrm{sin}\:\theta}{{b}}−\mathrm{1}}{\:\sqrt{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }}}=−{r} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{r}}=\frac{\mathrm{cos}\:\theta}{{a}}+\frac{\mathrm{sin}\:\theta}{{b}}+\sqrt{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }} \\ $$$$\frac{{d}\left(\frac{\mathrm{1}}{{r}}\right)}{{d}\theta}=−\frac{\mathrm{sin}\:\theta}{{a}}+\frac{\mathrm{cos}\:\theta}{{b}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{{a}}{{b}} \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\frac{{a}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }},\:\mathrm{cos}\:\theta=\frac{{b}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$$\Rightarrow\left(\frac{\mathrm{1}}{{r}}\right)_{{max}} =\frac{{b}}{{a}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}+\frac{{a}}{{b}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}+\sqrt{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }} \\ $$$$=\frac{\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{{ab}} \\ $$$$\Rightarrow{r}_{{min}} =\frac{{ab}}{\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$
Commented by ajfour last updated on 04/Apr/20
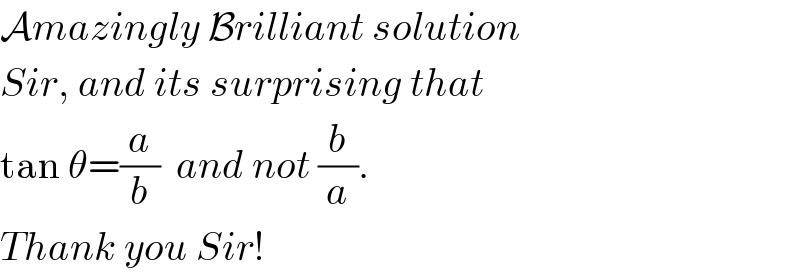
$$\mathcal{A}{mazingly}\:\mathcal{B}{rilliant}\:{solution} \\ $$$${Sir},\:{and}\:{its}\:{surprising}\:{that} \\ $$$$\mathrm{tan}\:\theta=\frac{{a}}{{b}}\:\:{and}\:{not}\:\frac{{b}}{{a}}. \\ $$$${Thank}\:{you}\:{Sir}! \\ $$
Commented by mr W last updated on 04/Apr/20
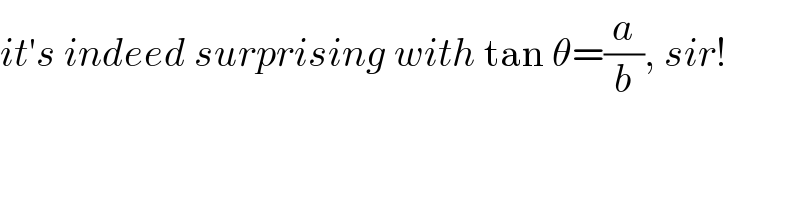
$${it}'{s}\:{indeed}\:{surprising}\:{with}\:\mathrm{tan}\:\theta=\frac{{a}}{{b}},\:{sir}! \\ $$
