Question Number 87511 by M±th+et£s last updated on 04/Apr/20
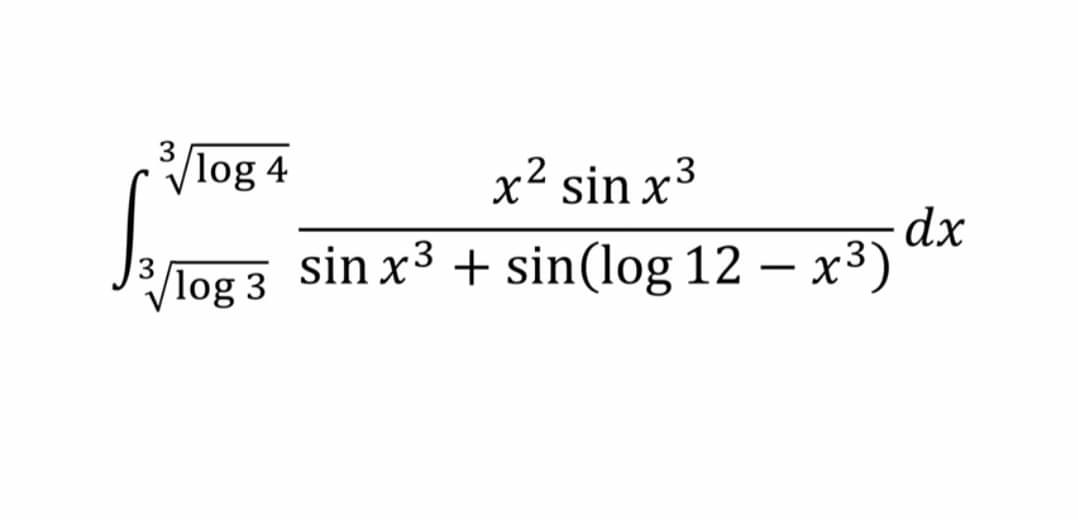
Answered by TANMAY PANACEA. last updated on 04/Apr/20
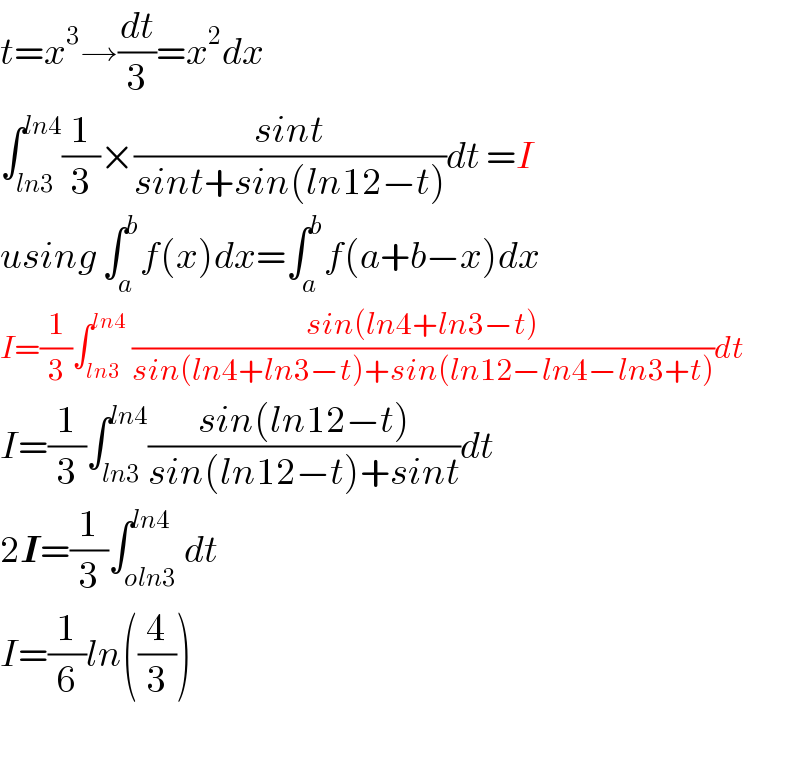
$${t}={x}^{\mathrm{3}} \rightarrow\frac{{dt}}{\mathrm{3}}={x}^{\mathrm{2}} {dx} \\ $$$$\int_{{ln}\mathrm{3}} ^{{ln}\mathrm{4}} \frac{\mathrm{1}}{\mathrm{3}}×\frac{{sint}}{{sint}+{sin}\left({ln}\mathrm{12}−{t}\right)}{dt}\:={I} \\ $$$${using}\:\int_{{a}} ^{{b}} {f}\left({x}\right){dx}=\int_{{a}} ^{{b}} {f}\left({a}+{b}−{x}\right){dx} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{3}}\int_{{ln}\mathrm{3}} ^{{ln}\mathrm{4}} \:\frac{{sin}\left({ln}\mathrm{4}+{ln}\mathrm{3}−{t}\right)}{{sin}\left({ln}\mathrm{4}+{ln}\mathrm{3}−{t}\right)+{sin}\left({ln}\mathrm{12}−{ln}\mathrm{4}−{ln}\mathrm{3}+{t}\right)}{dt} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{3}}\int_{{ln}\mathrm{3}} ^{{ln}\mathrm{4}} \frac{{sin}\left({ln}\mathrm{12}−{t}\right)}{{sin}\left({ln}\mathrm{12}−{t}\right)+{sint}}{dt} \\ $$$$\mathrm{2}\boldsymbol{{I}}=\frac{\mathrm{1}}{\mathrm{3}}\int_{{oln}\mathrm{3}} ^{{ln}\mathrm{4}} {dt} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{6}}{ln}\left(\frac{\mathrm{4}}{\mathrm{3}}\right) \\ $$$$ \\ $$
Commented by M±th+et£s last updated on 04/Apr/20

$${god}\:{bless}\:{you}\:{sir} \\ $$
Commented by TANMAY PANACEA. last updated on 04/Apr/20

$${thank}\:{you}\:{sir} \\ $$
Answered by redmiiuser last updated on 05/Apr/20
![sin x^3 +sin (log 12−x^3 ) =2sin( ((log 12)/2)).cos (x^3 −((log 12)/2)) x^3 −((log 12)/2)=t dt=3x^2 .dx (dt/3)=x^2 .dx sin x^3 =sin (t+((log 12)/2)) (1/(3.2sin (((log 12)/2))))∫_(log 3−((log 12)/2)) ^(log 4−((log 12)/2) ) ((sin (t+((log 12)/2)))/(cos t)).dt =(1/(6sin (((log 12)/2))))[cos ( ((log 12)/2)).∫_(log 3−((log 12)/2)) ^(log 4−((log 12)/2)) tan t.dt+sin (((log 12)/2))∫_(log 3−((log 12)/2)) ^(log 4−((log 12)/2)) dt] =((cot (((log 12)/2)))/6).[log ∣sec(t)∣]_(log 3−((log 12)/2)) ^(log 4 −((log 12)/2)) +(1/6)[t]_(log 3−((log 12)/2)) ^(log 4−((log 12)/2))](https://www.tinkutara.com/question/Q87579.png)
$$\mathrm{sin}\:{x}^{\mathrm{3}} +\mathrm{sin}\:\left(\mathrm{log}\:\mathrm{12}−{x}^{\mathrm{3}} \right) \\ $$$$=\mathrm{2sin}\left(\:\frac{\mathrm{log}\:\mathrm{12}}{\mathrm{2}}\right).\mathrm{cos}\:\left({x}^{\mathrm{3}} −\frac{\mathrm{log}\:\mathrm{12}}{\mathrm{2}}\right) \\ $$$${x}^{\mathrm{3}} −\frac{\mathrm{log}\:\mathrm{12}}{\mathrm{2}}={t} \\ $$$${dt}=\mathrm{3}{x}^{\mathrm{2}} .{dx} \\ $$$$\frac{{dt}}{\mathrm{3}}={x}^{\mathrm{2}} .{dx} \\ $$$$\mathrm{sin}\:{x}^{\mathrm{3}} =\mathrm{sin}\:\left({t}+\frac{\mathrm{log}\:\mathrm{12}}{\mathrm{2}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{3}.\mathrm{2sin}\:\left(\frac{\mathrm{log}\:\mathrm{12}}{\mathrm{2}}\right)}\int_{\mathrm{log}\:\mathrm{3}−\frac{\mathrm{log}\:\mathrm{12}}{\mathrm{2}}} ^{\mathrm{log}\:\mathrm{4}−\frac{\mathrm{log}\:\mathrm{12}}{\mathrm{2}}\:\:} \frac{\mathrm{sin}\:\left({t}+\frac{\mathrm{log}\:\mathrm{12}}{\mathrm{2}}\right)}{\mathrm{cos}\:{t}}.{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6sin}\:\left(\frac{\mathrm{log}\:\mathrm{12}}{\mathrm{2}}\right)}\left[\mathrm{cos}\:\left(\:\frac{\mathrm{log}\:\mathrm{12}}{\mathrm{2}}\right).\int_{\mathrm{log}\:\mathrm{3}−\frac{\mathrm{log}\:\mathrm{12}}{\mathrm{2}}} ^{{log}\:\mathrm{4}−\frac{\mathrm{log}\:\mathrm{12}}{\mathrm{2}}} \mathrm{tan}\:{t}.{dt}+\mathrm{sin}\:\left(\frac{\mathrm{log}\:\mathrm{12}}{\mathrm{2}}\right)\int_{\mathrm{log}\:\mathrm{3}−\frac{\mathrm{log}\:\mathrm{12}}{\mathrm{2}}} ^{\mathrm{log}\:\mathrm{4}−\frac{\mathrm{log}\:\mathrm{12}}{\mathrm{2}}} {dt}\right] \\ $$$$=\frac{\mathrm{cot}\:\left(\frac{\mathrm{log}\:\mathrm{12}}{\mathrm{2}}\right)}{\mathrm{6}}.\left[\mathrm{log}\:\mid{sec}\left({t}\right)\mid\right]_{\mathrm{log}\:\mathrm{3}−\frac{\mathrm{log}\:\mathrm{12}}{\mathrm{2}}} ^{\mathrm{log}\:\mathrm{4}\:−\frac{\mathrm{log}\:\mathrm{12}}{\mathrm{2}}} +\frac{\mathrm{1}}{\mathrm{6}}\left[{t}\right]_{\mathrm{log}\:\mathrm{3}−\frac{\mathrm{log}\:\mathrm{12}}{\mathrm{2}}} ^{\mathrm{log}\:\mathrm{4}−\frac{\mathrm{log}\:\mathrm{12}}{\mathrm{2}}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by redmiiuser last updated on 05/Apr/20
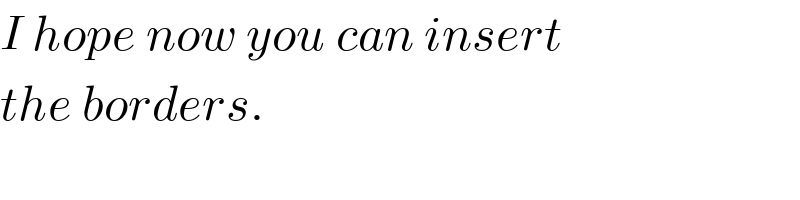
$${I}\:{hope}\:{now}\:{you}\:{can}\:{insert} \\ $$$${the}\:{borders}. \\ $$
Commented by M±th+et£s last updated on 05/Apr/20

$${thank}\:{you}\:{sir} \\ $$
Commented by redmiiuser last updated on 05/Apr/20

$${welcome} \\ $$
