Question Number 87538 by Power last updated on 04/Apr/20

Commented by mathmax by abdo last updated on 04/Apr/20
![I =∫_(−1) ^1 f^(−1) (x)dx changement f^(−1) (x)=t give x =f(t)⇒ dx =f^′ (t)dt ⇒ I =∫_(f^(−1) (−1)) ^(f^(−1) (1)) t f^′ (t)dt =_(by parts) =[(t^2 /2)f(t)]_(f^(−1) (−1)) ^(f^(−1) (1)) −∫_(f^(−1) (−1)) ^(f^(−1) (1)) (t^2 /2)f(t)dt =(1/2){ (f^(−1) (1))^2 + (f^(−1) (−1))^2 }−(1/2)∫_(f^(−1) (−1)) ^(f^(−1) (1)) t^2 (t^3 +t−1)dt we hsve ∫_(f^(−1) (−1)) ^(f^(−1) (1)) (t^5 +t^3 −t^2 )dt [(t^6 /6)+(t^4 /4)−(t^3 /3)]_(f^(−1) (−1)) ^(f^(−1) (1)) rest calculus of f^(−1) (1) and f^(−1) (−1) ...be continued...](https://www.tinkutara.com/question/Q87541.png)
$${I}\:=\int_{−\mathrm{1}} ^{\mathrm{1}} \:{f}^{−\mathrm{1}} \left({x}\right){dx}\:\:\:{changement}\:{f}^{−\mathrm{1}} \left({x}\right)={t}\:{give}\:{x}\:={f}\left({t}\right)\Rightarrow \\ $$$${dx}\:={f}^{'} \left({t}\right){dt}\:\Rightarrow\:{I}\:=\int_{{f}^{−\mathrm{1}} \left(−\mathrm{1}\right)} ^{{f}^{−\mathrm{1}} \left(\mathrm{1}\right)} \:{t}\:{f}^{'} \left({t}\right){dt}\:\:=_{{by}\:{parts}} \\ $$$$=\left[\frac{{t}^{\mathrm{2}} }{\mathrm{2}}{f}\left({t}\right)\right]_{{f}^{−\mathrm{1}} \left(−\mathrm{1}\right)} ^{{f}^{−\mathrm{1}} \left(\mathrm{1}\right)} \:−\int_{{f}^{−\mathrm{1}} \left(−\mathrm{1}\right)} ^{{f}^{−\mathrm{1}} \left(\mathrm{1}\right)} \:\frac{{t}^{\mathrm{2}} }{\mathrm{2}}{f}\left({t}\right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\left({f}^{−\mathrm{1}} \left(\mathrm{1}\right)\right)^{\mathrm{2}} +\:\left({f}^{−\mathrm{1}} \left(−\mathrm{1}\right)\right)^{\mathrm{2}} \right\}−\frac{\mathrm{1}}{\mathrm{2}}\int_{{f}^{−\mathrm{1}} \left(−\mathrm{1}\right)} ^{{f}^{−\mathrm{1}} \left(\mathrm{1}\right)} \:\:{t}^{\mathrm{2}} \left({t}^{\mathrm{3}} +{t}−\mathrm{1}\right){dt} \\ $$$${we}\:{hsve} \\ $$$$\int_{{f}^{−\mathrm{1}} \left(−\mathrm{1}\right)} ^{{f}^{−\mathrm{1}} \left(\mathrm{1}\right)} \left({t}^{\mathrm{5}} \:+{t}^{\mathrm{3}} −{t}^{\mathrm{2}} \right){dt} \\ $$$$\left[\frac{{t}^{\mathrm{6}} }{\mathrm{6}}+\frac{{t}^{\mathrm{4}} }{\mathrm{4}}−\frac{{t}^{\mathrm{3}} }{\mathrm{3}}\right]_{{f}^{−\mathrm{1}} \left(−\mathrm{1}\right)} ^{{f}^{−\mathrm{1}} \left(\mathrm{1}\right)} \:\:\:\:\:\:{rest}\:{calculus}\:{of}\:{f}^{−\mathrm{1}} \left(\mathrm{1}\right)\:{and}\:{f}^{−\mathrm{1}} \left(−\mathrm{1}\right) \\ $$$$…{be}\:{continued}… \\ $$
Commented by Power last updated on 04/Apr/20

$$\mathrm{sir}\:\mathrm{step}\:\mathrm{by}\:\mathrm{step}\:\mathrm{solution}\:\mathrm{please} \\ $$
Commented by MJS last updated on 04/Apr/20

$$\frac{\mathrm{5}}{\mathrm{4}} \\ $$
Commented by mathmax by abdo last updated on 04/Apr/20

$${let}\:{solve}\:{f}\left({x}\right)={y}\:\Rightarrow{x}^{\mathrm{3}} \:+{x}−\mathrm{1}\:={y}\:{let}\:{x}\:={u}+{v}\:\Rightarrow \\ $$$$\left({u}+{v}\right)^{\mathrm{3}} \:+{u}+{v}−\mathrm{1}−{y}\:=\mathrm{0}\:\Rightarrow{u}^{\mathrm{3}} \:+{v}^{\mathrm{3}} \:+\mathrm{3}{uv}\left({u}+{v}\right)\:+{u}+{v}\:−\mathrm{1}−{y}\:=\mathrm{0}\:\Rightarrow \\ $$$${u}^{\mathrm{3}} \:+{v}^{\mathrm{3}} \:−\mathrm{1}−{y}\:+\left({u}+{v}\right)\left(\mathrm{3}{uv}\:+\mathrm{1}\right)\:=\mathrm{0}\:\Rightarrow\begin{cases}{{u}^{\mathrm{3}} \:+{y}^{\mathrm{3}} =\mathrm{1}+{y}}\\{{uv}\:=−\frac{\mathrm{1}}{\mathrm{3}}}\end{cases} \\ $$$$\Rightarrow\:\begin{cases}{\:{u}^{\mathrm{3}} \:+{v}^{\mathrm{3}} \:=\mathrm{1}+{y}}\\{{u}^{\mathrm{3}} \:{v}^{\mathrm{3}} \:=−\frac{\mathrm{1}}{\mathrm{27}}}\end{cases} \\ $$$$\Rightarrow\:{u}^{\mathrm{3}} \:{and}\:{v}^{\mathrm{3}} \:{are}\:{solution}\:{of}\:{X}^{\mathrm{2}} −\left(\mathrm{1}+{y}\right){X}\:−\frac{\mathrm{1}}{\mathrm{27}}\:=\mathrm{0} \\ $$$$\Delta\:=\left(\mathrm{1}+{y}\right)^{\mathrm{2}} \:+\frac{\mathrm{4}}{\mathrm{27}}\:\Rightarrow{X}_{\mathrm{1}} =\frac{\mathrm{1}+{y}\:+\sqrt{\left(\mathrm{1}+{y}\right)^{\mathrm{2}} \:+\frac{\mathrm{4}}{\mathrm{27}}}}{\mathrm{2}} \\ $$$${X}_{\mathrm{2}} =\frac{\mathrm{1}+{y}−\sqrt{\left(\mathrm{1}+{y}\right)^{\mathrm{2}} +\frac{\mathrm{4}}{\mathrm{27}}}}{\mathrm{2}}\:\Rightarrow \\ $$$${u}\:=^{\mathrm{3}} \sqrt{\frac{\mathrm{1}+{y}+\sqrt{\left(\mathrm{1}+{y}\right)^{\mathrm{2}} \:+\frac{\mathrm{4}}{\mathrm{27}}}}{\mathrm{2}}}\:{and}\:{v}\:=^{\mathrm{3}} \sqrt{\frac{\mathrm{1}+{y}−\sqrt{\left(\mathrm{1}+{y}\right)^{\mathrm{2}} +\frac{\mathrm{4}}{\mathrm{27}}}}{\mathrm{2}}} \\ $$$${or}\:{u}\:=−^{\mathrm{3}} \sqrt{…}\:\:{and}\:{v}\:=−^{\mathrm{3}} \sqrt{….}\:\:\left(\:\:{uv}<\mathrm{0}\right)\:\Rightarrow \\ $$$${f}^{−\mathrm{1}} \left({x}\right)\:=^{\mathrm{3}} \sqrt{\frac{\mathrm{1}+{x}+\sqrt{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} \:+\frac{\mathrm{4}}{\mathrm{27}}}}{\mathrm{2}}}\:+^{\mathrm{3}} \sqrt{\frac{\mathrm{1}+{x}−\sqrt{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} +\frac{\mathrm{4}}{\mathrm{27}}}}{\mathrm{2}}} \\ $$$$\Rightarrow{f}^{−\mathrm{1}} \left(−\mathrm{1}\right)\:=^{\mathrm{3}} \sqrt{\frac{\mathrm{1}}{\mathrm{27}}}−^{\mathrm{3}} \sqrt{\frac{\mathrm{1}}{\mathrm{27}}}\:=\mathrm{0} \\ $$$${f}^{−\mathrm{1}} \left(\mathrm{1}\right)\:=^{\mathrm{3}} \sqrt{\frac{\mathrm{2}+\sqrt{\mathrm{4}+\frac{\mathrm{4}}{\mathrm{27}}}}{\mathrm{2}}}\:+^{\mathrm{3}} \sqrt{\frac{\mathrm{2}−\sqrt{\mathrm{4}+\frac{\mathrm{4}}{\mathrm{27}}}}{\mathrm{2}}} \\ $$
Commented by Power last updated on 05/Apr/20

$$\mathrm{sir}\:\mathrm{pls}\:\mathrm{solution} \\ $$
Commented by Power last updated on 05/Apr/20

$$\mathrm{Mjs}\:\:\mathrm{sir}\:\:\mathrm{5}/\mathrm{4}\:\:\mathrm{correct}\:\mathrm{answer} \\ $$
Commented by mathmax by abdo last updated on 05/Apr/20
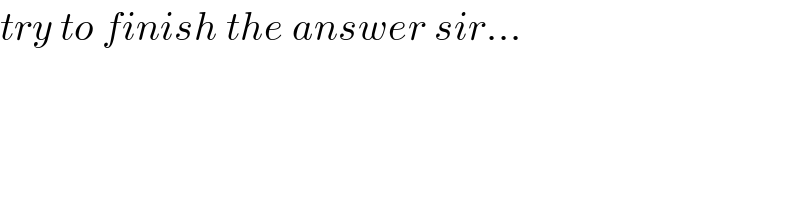
$${try}\:{to}\:{finish}\:{the}\:{answer}\:{sir}… \\ $$
