Question Number 87540 by Power last updated on 04/Apr/20
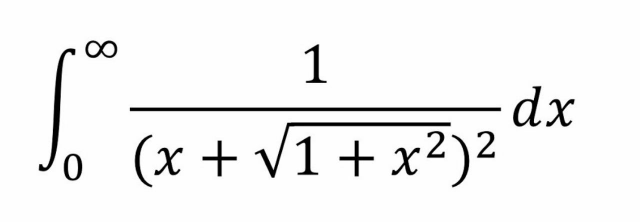
Commented by abdomathmax last updated on 05/Apr/20
![let I =∫_0 ^∞ (dx/((x+(√(1+x^2 )))^2 )) changement x =sh(t) give I =∫_0 ^∞ ((ch(t) dt)/((sh(t)+cht)^2 )) =∫_0 ^∞ ((ch(t))/e^(2t) )dt =∫_0 ^∞ e^(−2t) (((e^t +e^(−t) )/2))dt =(1/2)∫_0 ^∞ e^(−t) dt +(1/2)∫_0 ^∞ e^(−3t) dt =(1/2)[−e^(−t) ]_0 ^(+∞) +(1/2)[−(1/3)e^(−3t) ]_0 ^(+∞) =(1/2)(1) +(1/6) =(3/6)+(1/6) =(4/6) =(2/3)](https://www.tinkutara.com/question/Q87549.png)
$${let}\:\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} }\:{changement}\:{x}\:={sh}\left({t}\right)\:{give} \\ $$$${I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{ch}\left({t}\right)\:{dt}}{\left({sh}\left({t}\right)+{cht}\right)^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ch}\left({t}\right)}{{e}^{\mathrm{2}{t}} }{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:{e}^{−\mathrm{2}{t}} \left(\frac{{e}^{{t}} \:+{e}^{−{t}} }{\mathrm{2}}\right){dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:{e}^{−{t}} \:{dt}\:+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:{e}^{−\mathrm{3}{t}} \:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[−{e}^{−{t}} \right]_{\mathrm{0}} ^{+\infty} \:+\frac{\mathrm{1}}{\mathrm{2}}\left[−\frac{\mathrm{1}}{\mathrm{3}}{e}^{−\mathrm{3}{t}} \right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}\right)\:+\frac{\mathrm{1}}{\mathrm{6}}\:=\frac{\mathrm{3}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{6}}\:=\frac{\mathrm{4}}{\mathrm{6}}\:=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Answered by MJS last updated on 04/Apr/20
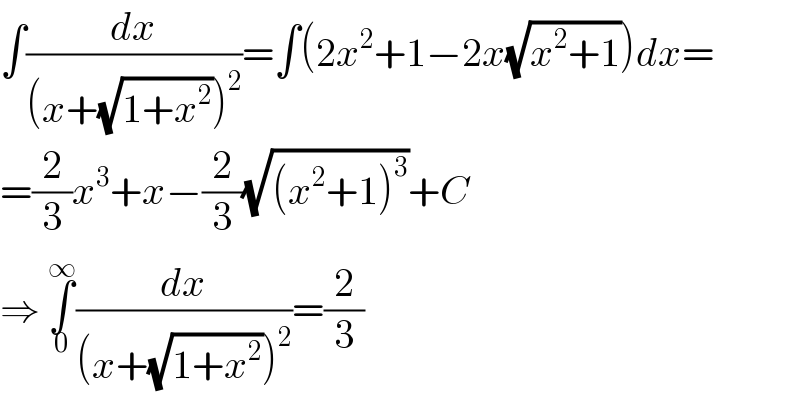
$$\int\frac{{dx}}{\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} }=\int\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right){dx}= \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}{x}^{\mathrm{3}} +{x}−\frac{\mathrm{2}}{\mathrm{3}}\sqrt{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }+{C} \\ $$$$\Rightarrow\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{dx}}{\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} }=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by Power last updated on 05/Apr/20
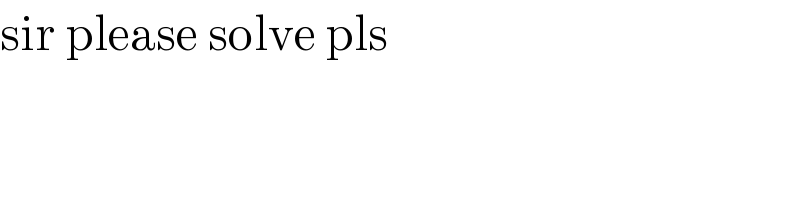
$$\mathrm{sir}\:\mathrm{please}\:\mathrm{solve}\:\mathrm{pls} \\ $$
