Menu Close

Question-87553

Tinku Tara 0 Comments
Pin




Question Number 87553 by TawaTawa1 last updated on 05/Apr/20
Answered by ajfour last updated on 05/Apr/20
let no. of boys in A=3k ...........girls .... A = 2k let no. of girls in B= x & no. of boys in B = y no. of girls in C = z no. of boys in C = t ⇒ x+y=5k ...(i) (x/4)+z=16+x ...(ii) (y/t)=(5/8) ....(iii) z+t=100 ....(iv) 10k+100=220 ...(v) Q=((3k+y+t)/(2k+x+z)) = ? from (v): k=12 ⇒ x+y=60 [using (i)] z=100−t y=((5t)/8) Now from (ii) (x/4)+100−t=16+x ⇒ ((3x)/4)+t=84 ...(I) x+((5t)/8)= 60 ....(II) ⇒ 336−4t+((15t)/8)=180 ((17t)/8)=156 but t shud hav been an integer! I shall checkgain afterawhile..
$${let}\:{no}.\:{of}\:{boys}\:{in}\:{A}=\mathrm{3}{k} \\ $$$$\:\:\:\:………..{girls}\:\:….\:{A}\:=\:\mathrm{2}{k} \\ $$$${let}\:\:{no}.\:{of}\:{girls}\:{in}\:{B}=\:{x} \\ $$$$\&\:\:\:{no}.\:{of}\:{boys}\:{in}\:{B}\:=\:{y} \\ $$$${no}.\:{of}\:{girls}\:{in}\:{C}\:=\:{z} \\ $$$${no}.\:{of}\:{boys}\:{in}\:{C}\:=\:{t} \\ $$$$\Rightarrow\:\:\:{x}+{y}=\mathrm{5}{k}\:\:\:\:…\left({i}\right) \\ $$$$\frac{{x}}{\mathrm{4}}+{z}=\mathrm{16}+{x}\:\:\:\:\:…\left({ii}\right) \\ $$$$\frac{{y}}{{t}}=\frac{\mathrm{5}}{\mathrm{8}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\left({iii}\right) \\ $$$${z}+{t}=\mathrm{100}\:\:\:\:\:\:\:\:\:\:\:….\left({iv}\right) \\ $$$$\mathrm{10}{k}+\mathrm{100}=\mathrm{220}\:\:\:\:…\left({v}\right) \\ $$$${Q}=\frac{\mathrm{3}{k}+{y}+{t}}{\mathrm{2}{k}+{x}+{z}}\:=\:? \\ $$$${from}\:\left({v}\right):\:\:\:\:{k}=\mathrm{12} \\ $$$$\Rightarrow\:\:{x}+{y}=\mathrm{60}\:\:\:\:\:\left[{using}\:\left({i}\right)\right] \\ $$$$\:\:\:\:\:\:\:{z}=\mathrm{100}−{t} \\ $$$$\:\:\:\:\:\:\:{y}=\frac{\mathrm{5}{t}}{\mathrm{8}} \\ $$$${Now}\:{from}\:\left({ii}\right) \\ $$$$\:\:\frac{{x}}{\mathrm{4}}+\mathrm{100}−{t}=\mathrm{16}+{x} \\ $$$$\Rightarrow\:\:\:\frac{\mathrm{3}{x}}{\mathrm{4}}+{t}=\mathrm{84}\:\:\:\:\:\:\:\:…\left({I}\right) \\ $$$$\:\:\:\:\:\:\:{x}+\frac{\mathrm{5}{t}}{\mathrm{8}}=\:\mathrm{60}\:\:\:\:\:\:….\left({II}\right) \\ $$$$\Rightarrow\:\:\:\mathrm{336}−\mathrm{4}{t}+\frac{\mathrm{15}{t}}{\mathrm{8}}=\mathrm{180} \\ $$$$\frac{\mathrm{17}{t}}{\mathrm{8}}=\mathrm{156}\:\:\:\: \\ $$$${but}\:\:{t}\:{shud}\:{hav}\:{been}\:{an}\:{integer}! \\ $$$${I}\:{shall}\:{checkgain}\:{afterawhile}.. \\ $$
Commented by TawaTawa1 last updated on 05/Apr/20
God bless you sir. I appreciate. From your solution sir. I got 7 : 4
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$$$\mathrm{From}\:\mathrm{your}\:\mathrm{solution}\:\mathrm{sir}.\:\:\mathrm{I}\:\mathrm{got}\:\:\:\:\:\:\mathrm{7}\::\:\mathrm{4} \\ $$
Commented by TawaTawa1 last updated on 05/Apr/20
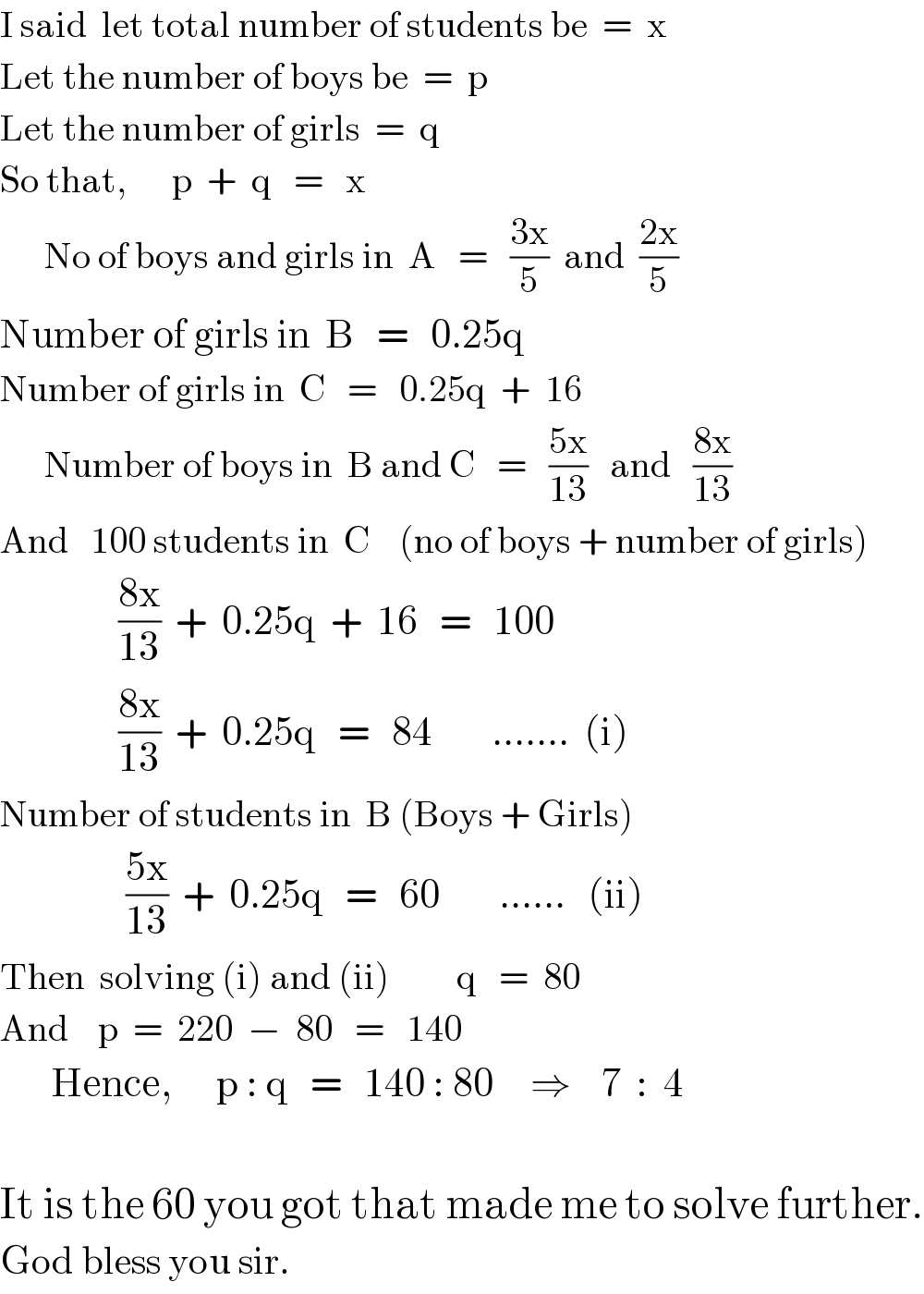
I said let total number of students be = x Let the number of boys be = p Let the number of girls = q So that, p + q = x No of boys and girls in A = ((3x)/5) and ((2x)/5) Number of girls in B = 0.25q Number of girls in C = 0.25q + 16 Number of boys in B and C = ((5x)/(13)) and ((8x)/(13)) And 100 students in C (no of boys + number of girls) ((8x)/(13)) + 0.25q + 16 = 100 ((8x)/(13)) + 0.25q = 84 ....... (i) Number of students in B (Boys + Girls) ((5x)/(13)) + 0.25q = 60 ...... (ii) Then solving (i) and (ii) q = 80 And p = 220 − 80 = 140 Hence, p : q = 140 : 80 ⇒ 7 : 4 It is the 60 you got that made me to solve further. God bless you sir.
$$\mathrm{I}\:\mathrm{said}\:\:\mathrm{let}\:\mathrm{total}\:\mathrm{number}\:\mathrm{of}\:\mathrm{students}\:\mathrm{be}\:\:=\:\:\mathrm{x} \\ $$$$\mathrm{Let}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{boys}\:\mathrm{be}\:\:=\:\:\mathrm{p} \\ $$$$\mathrm{Let}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{girls}\:\:=\:\:\mathrm{q} \\ $$$$\mathrm{So}\:\mathrm{that},\:\:\:\:\:\:\mathrm{p}\:\:+\:\:\mathrm{q}\:\:\:=\:\:\:\mathrm{x} \\ $$$$\:\:\:\:\:\:\mathrm{No}\:\mathrm{of}\:\mathrm{boys}\:\mathrm{and}\:\mathrm{girls}\:\mathrm{in}\:\:\mathrm{A}\:\:\:=\:\:\:\frac{\mathrm{3x}}{\mathrm{5}}\:\:\mathrm{and}\:\:\frac{\mathrm{2x}}{\mathrm{5}} \\ $$$$\mathrm{Number}\:\mathrm{of}\:\mathrm{girls}\:\mathrm{in}\:\:\mathrm{B}\:\:\:=\:\:\:\mathrm{0}.\mathrm{25q} \\ $$$$\mathrm{Number}\:\mathrm{of}\:\mathrm{girls}\:\mathrm{in}\:\:\mathrm{C}\:\:\:=\:\:\:\mathrm{0}.\mathrm{25q}\:\:+\:\:\mathrm{16} \\ $$$$\:\:\:\:\:\:\mathrm{Number}\:\mathrm{of}\:\mathrm{boys}\:\mathrm{in}\:\:\mathrm{B}\:\mathrm{and}\:\mathrm{C}\:\:\:=\:\:\:\frac{\mathrm{5x}}{\mathrm{13}}\:\:\:\mathrm{and}\:\:\:\frac{\mathrm{8x}}{\mathrm{13}} \\ $$$$\mathrm{And}\:\:\:\mathrm{100}\:\mathrm{students}\:\mathrm{in}\:\:\mathrm{C}\:\:\:\:\left(\mathrm{no}\:\mathrm{of}\:\mathrm{boys}\:+\:\mathrm{number}\:\mathrm{of}\:\mathrm{girls}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{8x}}{\mathrm{13}}\:\:+\:\:\mathrm{0}.\mathrm{25q}\:\:+\:\:\mathrm{16}\:\:\:=\:\:\:\mathrm{100}\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{8x}}{\mathrm{13}}\:\:+\:\:\mathrm{0}.\mathrm{25q}\:\:\:=\:\:\:\mathrm{84}\:\:\:\:\:\:\:\:…….\:\:\left(\mathrm{i}\right) \\ $$$$\mathrm{Number}\:\mathrm{of}\:\mathrm{students}\:\mathrm{in}\:\:\mathrm{B}\:\left(\mathrm{Boys}\:+\:\mathrm{Girls}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{5x}}{\mathrm{13}}\:\:+\:\:\mathrm{0}.\mathrm{25q}\:\:\:=\:\:\:\mathrm{60}\:\:\:\:\:\:\:\:……\:\:\:\left(\mathrm{ii}\right) \\ $$$$\mathrm{Then}\:\:\mathrm{solving}\:\left(\mathrm{i}\right)\:\mathrm{and}\:\left(\mathrm{ii}\right)\:\:\:\:\:\:\:\:\:\mathrm{q}\:\:\:=\:\:\mathrm{80} \\ $$$$\mathrm{And}\:\:\:\:\mathrm{p}\:\:=\:\:\mathrm{220}\:\:−\:\:\mathrm{80}\:\:\:=\:\:\:\mathrm{140} \\ $$$$\:\:\:\:\:\:\:\mathrm{Hence},\:\:\:\:\:\:\mathrm{p}\::\:\mathrm{q}\:\:\:=\:\:\:\mathrm{140}\::\:\mathrm{80}\:\:\:\:\:\Rightarrow\:\:\:\:\mathrm{7}\:\::\:\:\mathrm{4} \\ $$$$ \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{the}\:\mathrm{60}\:\mathrm{you}\:\mathrm{got}\:\mathrm{that}\:\mathrm{made}\:\mathrm{me}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{further}. \\ $$$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *