Menu Close

Question-87581

Tinku Tara 0 Comments
Pin




Question Number 87581 by peter frank last updated on 05/Apr/20
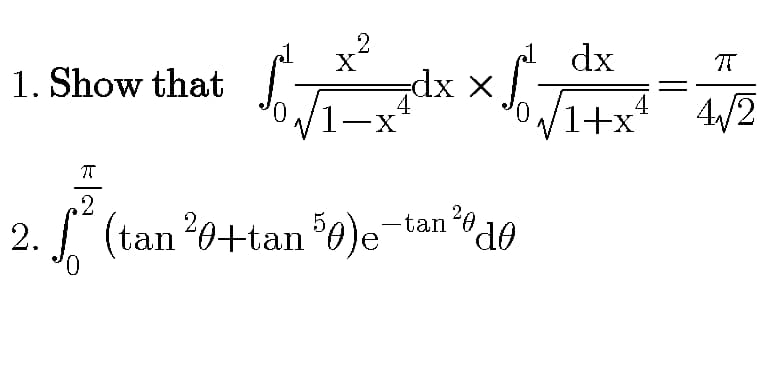
Commented by TANMAY PANACEA. last updated on 05/Apr/20
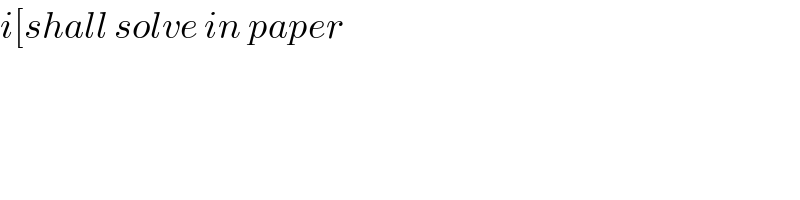
i[shall solve in paper
$${i}\left[{shall}\:{solve}\:{in}\:{paper}\right. \\ $$
Answered by TANMAY PANACEA. last updated on 05/Apr/20
1)∫_0 ^1 ((x^2 dx)/( (√(1−x^4 ))))dx×∫_0 ^1 (dx/( (√(1+x^4 )))) I=I_1 ×I_2 I_1 =∫_0 ^1 ((x^2 dx)/( (√(1−x^4 )))) x^2 =sina →2xdx=cosada ∫_0 ^(π/2) ((sina)/(cosa))×((cosada)/(2(√(sina))))=(1/2)∫_0 ^(π/2) (sina)^(2×(3/4)−1) (cosa)^(2×(1/2)−1) da using gamma function 2∫_0 ^(π/2) (sinα)^(2p−1) (cosα)^(2q−1) dα=((⌈(p)⌈(q))/(⌈(p+q))) I_1 =(1/4)×2∫_0 ^(π/2) (sina)^(2×(3/4)−1) (cosa)^(2×(1/2)−1) da =(1/4)×((⌈((3/4))⌈((1/2)))/(⌈((3/4)+(1/2)))) I_2 =∫_0 ^1 (dx/( (√(1+x^4 )))) x^2 =tanb→2xdx=sec^2 b db dx=((sec^2 b)/(2(√(tanb))))db ∫_0 ^(π/4) ((sec^2 b)/(2(√(tanb)) ×secb))db=(1/2)∫_0 ^(π/4) (db/( (√(sinbcosb))))=(1/( (√2)))∫_0 ^(π/4) (db/( (√(sin2b)))) ★★now t=2b dt=2db I_2 =(1/( (√2)))∫_0 ^(π/4) (db/( (√(sin2b))))=(1/( (√2)))∫_0 ^(π/2) (dt/(2(√(sint)))) =(1/(4(√2)))×2∫_0 ^(π/2) (sint)^(2×(1/4)−1) (cost)^(2×(1/2)−1) dt =(1/(4(√2)))×((⌈((1/4))⌈((1/2)))/(⌈((1/2)+(1/4))))=I_2 I=I_1 ×I_2 =(1/4)×((⌈((3/4))⌈((1/2)))/(⌈((5/4))))×(1/(4(√2)))×((⌈((1/4))⌈((1/2)))/(⌈((3/4)))) formula ⌈((1/2))=(√π) ⌈(p)⌈(1−p)=(p/(sinpπ)) I=(1/(16(√2)))×π×((⌈((1/4)))/(⌈(1+(1/4))))=(π/(16(√2)))×((⌈((1/4)))/((1/4)⌈((1/4)))) =(π/(4(√2))) proved note ⌈(n+1)=n⌈(n) so ⌈((5/4)) =⌈(1+(1/4))=(1/4)⌈((1/4))
$$\left.\mathrm{1}\right)\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} {dx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}{dx}×\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{4}} }} \\ $$$${I}={I}_{\mathrm{1}} ×{I}_{\mathrm{2}} \\ $$$${I}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} {dx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}\: \\ $$$${x}^{\mathrm{2}} ={sina}\:\:\rightarrow\mathrm{2}{xdx}={cosada} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sina}}{{cosa}}×\frac{{cosada}}{\mathrm{2}\sqrt{{sina}}}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({sina}\right)^{\mathrm{2}×\frac{\mathrm{3}}{\mathrm{4}}−\mathrm{1}} \left({cosa}\right)^{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} {da} \\ $$$${using}\:{gamma}\:{function} \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({sin}\alpha\right)^{\mathrm{2}{p}−\mathrm{1}} \left({cos}\alpha\right)^{\mathrm{2}{q}−\mathrm{1}} {d}\alpha=\frac{\lceil\left({p}\right)\lceil\left({q}\right)}{\lceil\left({p}+{q}\right)} \\ $$$${I}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{4}}×\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({sina}\right)^{\mathrm{2}×\frac{\mathrm{3}}{\mathrm{4}}−\mathrm{1}} \left({cosa}\right)^{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} {da} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}×\frac{\lceil\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\lceil\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\lceil\left(\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$${I}_{\mathrm{2}} =\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{4}} }} \\ $$$${x}^{\mathrm{2}} ={tanb}\rightarrow\mathrm{2}{xdx}={sec}^{\mathrm{2}} {b}\:{db} \\ $$$${dx}=\frac{{sec}^{\mathrm{2}} {b}}{\mathrm{2}\sqrt{{tanb}}}{db} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{sec}^{\mathrm{2}} {b}}{\mathrm{2}\sqrt{{tanb}}\:×{secb}}{db}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{db}}{\:\sqrt{{sinbcosb}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{db}}{\:\sqrt{{sin}\mathrm{2}{b}}} \\ $$$$\bigstar\bigstar{now}\:{t}=\mathrm{2}{b}\:\:{dt}=\mathrm{2}{db} \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{db}}{\:\sqrt{{sin}\mathrm{2}{b}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dt}}{\mathrm{2}\sqrt{{sint}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}×\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({sint}\right)^{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} \left({cost}\right)^{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} {dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}×\frac{\lceil\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\lceil\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\lceil\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\right)}={I}_{\mathrm{2}} \\ $$$${I}={I}_{\mathrm{1}} ×{I}_{\mathrm{2}} \\ $$$$\:=\frac{\mathrm{1}}{\mathrm{4}}×\frac{\lceil\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\lceil\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\lceil\left(\frac{\mathrm{5}}{\mathrm{4}}\right)}×\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}×\frac{\lceil\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\lceil\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\lceil\left(\frac{\mathrm{3}}{\mathrm{4}}\right)} \\ $$$${formula}\:\lceil\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\sqrt{\pi}\: \\ $$$$\lceil\left({p}\right)\lceil\left(\mathrm{1}−{p}\right)=\frac{{p}}{{sinp}\pi} \\ $$$$\boldsymbol{{I}}=\frac{\mathrm{1}}{\mathrm{16}\sqrt{\mathrm{2}}}×\pi×\frac{\lceil\left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\lceil\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\right)}=\frac{\pi}{\mathrm{16}\sqrt{\mathrm{2}}}×\frac{\lceil\left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\frac{\mathrm{1}}{\mathrm{4}}\lceil\left(\frac{\mathrm{1}}{\mathrm{4}}\right)} \\ $$$$=\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\:\:{proved} \\ $$$$ \\ $$$${note}\:\lceil\left({n}+\mathrm{1}\right)={n}\lceil\left({n}\right) \\ $$$${so}\:\lceil\left(\frac{\mathrm{5}}{\mathrm{4}}\right) \\ $$$$=\lceil\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\right)=\frac{\mathrm{1}}{\mathrm{4}}\lceil\left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$ \\ $$$$ \\ $$
Answered by TANMAY PANACEA. last updated on 05/Apr/20
2)∫_0 ^(π/2) (tan^2 θ+tan^5 θ)e^(−tan^2 θ) dθ t=tan^2 θ (dt/dθ)=2tanθ×sec^2 θ=2tanθ(1+tan^2 θ)=2(√t) (1+t) ∫_0 ^∞ (t+t^(5/2) )e^(−t) ×2((√t) +t^(3/2) )dt I=2∫_0 ^∞ e^(−t) (t^(3/2) +t^(5/2) +t^3 +t^4 )dt formula ⌈(n)=∫_0 ^∞ e^(−x) ×x^(n−1) dx (I/2)=∫_0 ^∞ e^(−t) .t^((5/2)−1) +∫_0 ^∞ e^(−t) .t^((7/2)−1) +∫_0 ^∞ e^(−t) .t^(4−1) +∫_0 ^∞ e^(−t) .t^(5−1) =⌈((5/2))+⌈((7/2))+⌈(4)+⌈(5) ⌈((5/2))=⌈((3/2)+1)=(3/2)×(1/2)×(√π) =((3(√π))/4) ⌈((7/2))=(5/2)×(3/2)×(1/2)×(√π) =((15)/8)(√π) ⌈(4)=3×2×1=6 ⌈(5)=4×3×2×1=24 I=2[((3(√π))/4)+((15(√π))/8)+6+24] pls check...
$$\left.\mathrm{2}\right)\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left({tan}^{\mathrm{2}} \theta+{tan}^{\mathrm{5}} \theta\right){e}^{−{tan}^{\mathrm{2}} \theta} {d}\theta \\ $$$${t}={tan}^{\mathrm{2}} \theta \\ $$$$\frac{{dt}}{{d}\theta}=\mathrm{2}{tan}\theta×{sec}^{\mathrm{2}} \theta=\mathrm{2}{tan}\theta\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)=\mathrm{2}\sqrt{{t}}\:\left(\mathrm{1}+{t}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \left({t}+{t}^{\frac{\mathrm{5}}{\mathrm{2}}} \right){e}^{−{t}} ×\mathrm{2}\left(\sqrt{{t}}\:+{t}^{\frac{\mathrm{3}}{\mathrm{2}}} \right){dt} \\ $$$${I}=\mathrm{2}\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} \left({t}^{\frac{\mathrm{3}}{\mathrm{2}}} +{t}^{\frac{\mathrm{5}}{\mathrm{2}}} +{t}^{\mathrm{3}} +{t}^{\mathrm{4}} \right){dt} \\ $$$${formula}\:\lceil\left({n}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} ×{x}^{{n}−\mathrm{1}} {dx} \\ $$$$\frac{{I}}{\mathrm{2}}=\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} .{t}^{\frac{\mathrm{5}}{\mathrm{2}}−\mathrm{1}} +\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} .{t}^{\frac{\mathrm{7}}{\mathrm{2}}−\mathrm{1}} +\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} .{t}^{\mathrm{4}−\mathrm{1}} +\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} .{t}^{\mathrm{5}−\mathrm{1}} \\ $$$$=\lceil\left(\frac{\mathrm{5}}{\mathrm{2}}\right)+\lceil\left(\frac{\mathrm{7}}{\mathrm{2}}\right)+\lceil\left(\mathrm{4}\right)+\lceil\left(\mathrm{5}\right) \\ $$$$\lceil\left(\frac{\mathrm{5}}{\mathrm{2}}\right)=\lceil\left(\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{1}\right)=\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}×\sqrt{\pi}\:=\frac{\mathrm{3}\sqrt{\pi}}{\mathrm{4}} \\ $$$$\lceil\left(\frac{\mathrm{7}}{\mathrm{2}}\right)=\frac{\mathrm{5}}{\mathrm{2}}×\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}×\sqrt{\pi}\:=\frac{\mathrm{15}}{\mathrm{8}}\sqrt{\pi}\: \\ $$$$\lceil\left(\mathrm{4}\right)=\mathrm{3}×\mathrm{2}×\mathrm{1}=\mathrm{6} \\ $$$$\lceil\left(\mathrm{5}\right)=\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}=\mathrm{24} \\ $$$${I}=\mathrm{2}\left[\frac{\mathrm{3}\sqrt{\pi}}{\mathrm{4}}+\frac{\mathrm{15}\sqrt{\pi}}{\mathrm{8}}+\mathrm{6}+\mathrm{24}\right] \\ $$$${pls}\:{check}… \\ $$$$ \\ $$
Commented by peter frank last updated on 15/Apr/20
correct sir thank you
$${correct}\:{sir}\:{thank}\:{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *