Question Number 87585 by Power last updated on 05/Apr/20
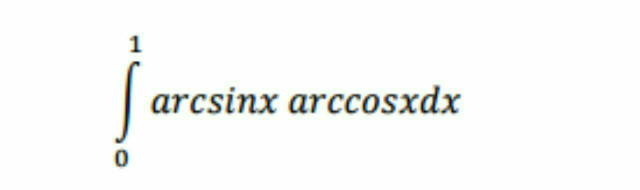
Answered by redmiiuser last updated on 05/Apr/20
![arcsin x+arccos x=(π/2) arcsin x.arccos x=(π/2)arcsin x−(arcsin x)^2 arcsin x=t dx=cos t.dt x=sin t ∫_0 ^(π/2) ((π/2)t−t^2 )cos t.dt =(π/2)∫_0 ^(π/2) tcos t.dt−∫_0 ^(π/2) t^2 cos t.dt =(π/2)[t∫_0 ^(π/2) cos t.dt−∫_(0 ) ^(π/2) {∫_0 ^(π/2) cos t.dt}.dt]−[∫_0 ^(π/2) cos t.dt−∫_0 ^(π/2) 2tsin t.dt] =(π/2)[tsin t+cos t]_0 ^(π/2) −[t^2 sin t+2tcos t−2sin t]_0 ^(π/2) =(π/2)[(π/2)−1]−[(π^2 /4)−2] =2−(π/2)](https://www.tinkutara.com/question/Q87635.png)
$${arc}\mathrm{sin}\:{x}+\mathrm{arccos}\:{x}=\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{arcsin}\:{x}.\mathrm{arccos}\:{x}=\frac{\pi}{\mathrm{2}}\mathrm{arcsin}\:{x}−\left(\mathrm{arcsin}\:{x}\right)^{\mathrm{2}} \\ $$$$\mathrm{arcsin}\:{x}={t} \\ $$$${dx}=\mathrm{cos}\:{t}.{dt} \\ $$$${x}=\mathrm{sin}\:{t} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{\pi}{\mathrm{2}}{t}−{t}^{\mathrm{2}} \right)\mathrm{cos}\:{t}.{dt} \\ $$$$=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {t}\mathrm{cos}\:{t}.{dt}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {t}^{\mathrm{2}} \mathrm{cos}\:{t}.{dt} \\ $$$$=\frac{\pi}{\mathrm{2}}\left[{t}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}\:{t}.{dt}−\int_{\mathrm{0}\:} ^{\frac{\pi}{\mathrm{2}}} \left\{\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}\:{t}.{dt}\right\}.{dt}\right]−\left[\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}\:{t}.{dt}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{2}{t}\mathrm{sin}\:{t}.{dt}\right] \\ $$$$=\frac{\pi}{\mathrm{2}}\left[{t}\mathrm{sin}\:{t}+\mathrm{cos}\:{t}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −\left[{t}^{\mathrm{2}} \mathrm{sin}\:{t}+\mathrm{2}{t}\mathrm{cos}\:{t}−\mathrm{2sin}\:{t}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\frac{\pi}{\mathrm{2}}\left[\frac{\pi}{\mathrm{2}}−\mathrm{1}\right]−\left[\frac{\pi^{\mathrm{2}} }{\mathrm{4}}−\mathrm{2}\right] \\ $$$$=\mathrm{2}−\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 05/Apr/20

$${nice}\:{method}! \\ $$
