Question Number 87716 by Power last updated on 05/Apr/20

Commented by malwaan last updated on 05/Apr/20
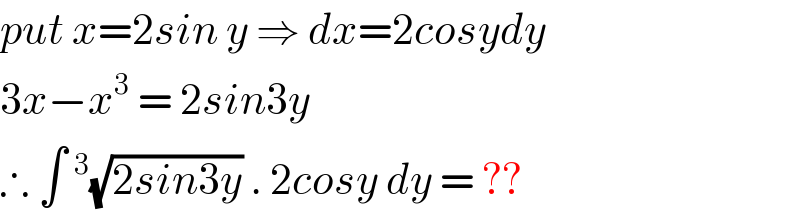
$${put}\:{x}=\mathrm{2}{sin}\:{y}\:\Rightarrow\:{dx}=\mathrm{2}{cosydy} \\ $$$$\mathrm{3}{x}−{x}^{\mathrm{3}} \:=\:\mathrm{2}{sin}\mathrm{3}{y} \\ $$$$\therefore\:\int\:^{\mathrm{3}} \sqrt{\mathrm{2}{sin}\mathrm{3}{y}}\:.\:\mathrm{2}{cosy}\:{dy}\:=\:?? \\ $$
Answered by MJS last updated on 06/Apr/20
![∫(3x−x^3 )^(1/3) dx=−∫x^(1/3) (x^2 −3)^(1/3) dx= [t=(x^(2/3) /((x^2 −3)^(1/3) )) ⇔ x=(((√3)t^(3/2) )/((t^3 −1)^(1/2) )) → dx=−(1/2)x^(1/3) (x^2 −3)^(4/3) dt] =(9/2)∫(t/((t^3 −1)^2 ))dt= [Ostrogradski, like I have shown before] =−((3t^2 )/(2(t^3 −1)))−(3/2)∫(t/(t^3 −1))dt ∫(t/(t^3 −1))dt=−(1/3)∫((t−1)/(t^2 +t+1))dt+(1/3)∫(dt/(t−1))= =−(1/6)ln (t^2 +t+1) +((√3)/3)arctan (((√3)(2t+1))/3) +(1/3)ln (t−1) = =(1/6)ln (((t−1)^2 )/(t^2 +t+1)) +((√3)/3)arctan (((√3)(2t+1))/3) =−((3t^2 )/(2(t^3 −1)))+(1/4)ln ((t^2 +t+1)/((t−1)^2 )) −((√3)/2)arctan (((√3)(2t+1))/3) now insert t=(x^(2/3) /((x^2 −3)^(1/3) ))](https://www.tinkutara.com/question/Q87753.png)
$$\int\left(\mathrm{3}{x}−{x}^{\mathrm{3}} \right)^{\mathrm{1}/\mathrm{3}} {dx}=−\int{x}^{\mathrm{1}/\mathrm{3}} \left({x}^{\mathrm{2}} −\mathrm{3}\right)^{\mathrm{1}/\mathrm{3}} {dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{{x}^{\mathrm{2}/\mathrm{3}} }{\left({x}^{\mathrm{2}} −\mathrm{3}\right)^{\mathrm{1}/\mathrm{3}} }\:\Leftrightarrow\:{x}=\frac{\sqrt{\mathrm{3}}{t}^{\mathrm{3}/\mathrm{2}} }{\left({t}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{1}/\mathrm{2}} }\:\rightarrow\:{dx}=−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{1}/\mathrm{3}} \left({x}^{\mathrm{2}} −\mathrm{3}\right)^{\mathrm{4}/\mathrm{3}} {dt}\right] \\ $$$$=\frac{\mathrm{9}}{\mathrm{2}}\int\frac{{t}}{\left({t}^{\mathrm{3}} −\mathrm{1}\right)^{\mathrm{2}} }{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski},\:\mathrm{like}\:\mathrm{I}\:\mathrm{have}\:\mathrm{shown}\:\mathrm{before}\right] \\ $$$$=−\frac{\mathrm{3}{t}^{\mathrm{2}} }{\mathrm{2}\left({t}^{\mathrm{3}} −\mathrm{1}\right)}−\frac{\mathrm{3}}{\mathrm{2}}\int\frac{{t}}{{t}^{\mathrm{3}} −\mathrm{1}}{dt} \\ $$$$ \\ $$$$\:\:\:\:\:\int\frac{{t}}{{t}^{\mathrm{3}} −\mathrm{1}}{dt}=−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{t}−\mathrm{1}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{dt}+\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dt}}{{t}−\mathrm{1}}= \\ $$$$\:\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\:\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)\:+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{t}+\mathrm{1}\right)}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\left({t}−\mathrm{1}\right)\:= \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\:\frac{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }{{t}^{\mathrm{2}} +{t}+\mathrm{1}}\:+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{t}+\mathrm{1}\right)}{\mathrm{3}} \\ $$$$ \\ $$$$=−\frac{\mathrm{3}{t}^{\mathrm{2}} }{\mathrm{2}\left({t}^{\mathrm{3}} −\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\frac{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{t}+\mathrm{1}\right)}{\mathrm{3}} \\ $$$$\mathrm{now}\:\mathrm{insert}\:{t}=\frac{{x}^{\mathrm{2}/\mathrm{3}} }{\left({x}^{\mathrm{2}} −\mathrm{3}\right)^{\mathrm{1}/\mathrm{3}} } \\ $$
