Question-87803

Question Number 87803 by ajfour last updated on 06/Apr/20

Commented by ajfour last updated on 06/Apr/20

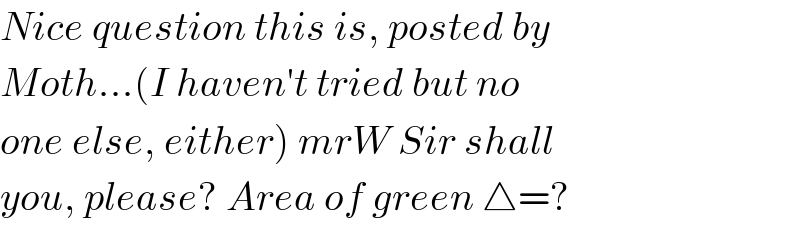
Nice question this is, posted by Moth...(I haven′t tried but no one else, either) mrW Sir shall you, please? Area of green △=?

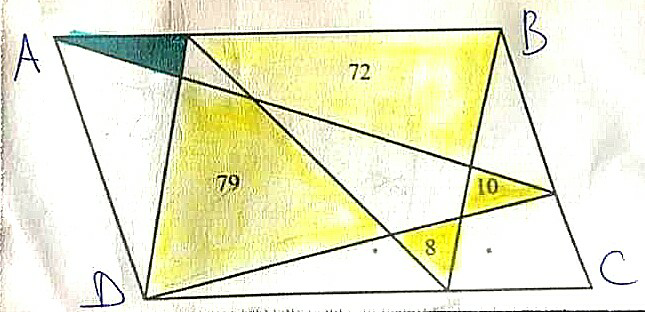
$${Nice}\:{question}\:{this}\:{is},\:{posted}\:{by} \\ $$$${Moth}…\left({I}\:{haven}'{t}\:{tried}\:{but}\:{no}\right. \\ $$$$\left.{one}\:{else},\:{either}\right)\:{mrW}\:{Sir}\:{shall} \\ $$$${you},\:{please}?\:{Area}\:{of}\:{green}\:\bigtriangleup=? \\ $$

Commented by john santu last updated on 06/Apr/20

$$\mathrm{9}\: \\ $$

Commented by ajfour last updated on 06/Apr/20

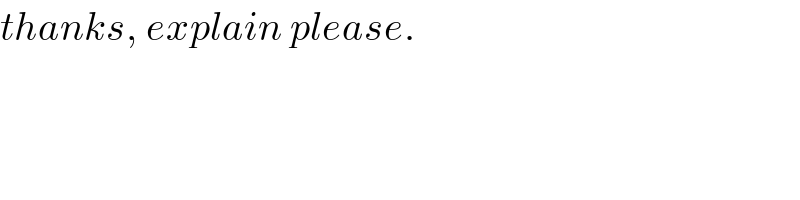
$${thanks},\:{explain}\:{please}. \\ $$

Commented by M±th+et£s last updated on 06/Apr/20

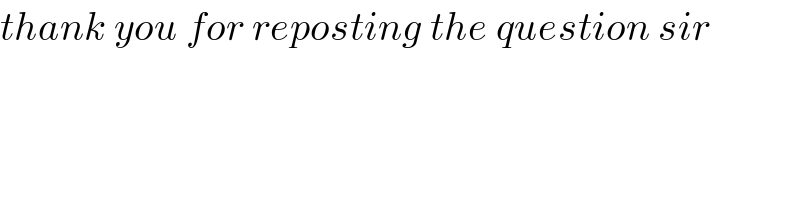
$${thank}\:{you}\:{for}\:{reposting}\:{the}\:{question}\:{sir} \\ $$

Answered by M±th+et£s last updated on 06/Apr/20

[ADM]+[MLB]=(1/2)[ABCD]=[AND] ⇒([APM]+[APD])+(72+[QSTR]+8) =[APD]+79+[QSTR]+10 [APM]=(79+10)−(72+8) =9

$$\left[{ADM}\right]+\left[{MLB}\right]=\frac{\mathrm{1}}{\mathrm{2}}\left[{ABCD}\right]=\left[{AND}\right] \\ $$$$\Rightarrow\left(\left[{APM}\right]+\left[{APD}\right]\right)+\left(\mathrm{72}+\left[{QSTR}\right]+\mathrm{8}\right) \\ $$$$=\left[{APD}\right]+\mathrm{79}+\left[{QSTR}\right]+\mathrm{10} \\ $$$$\left[{APM}\right]=\left(\mathrm{79}+\mathrm{10}\right)−\left(\mathrm{72}+\mathrm{8}\right) \\ $$$$=\mathrm{9} \\ $$

Commented by ajfour last updated on 06/Apr/20