Question Number 87886 by TawaTawa1 last updated on 06/Apr/20

Commented by jagoll last updated on 07/Apr/20
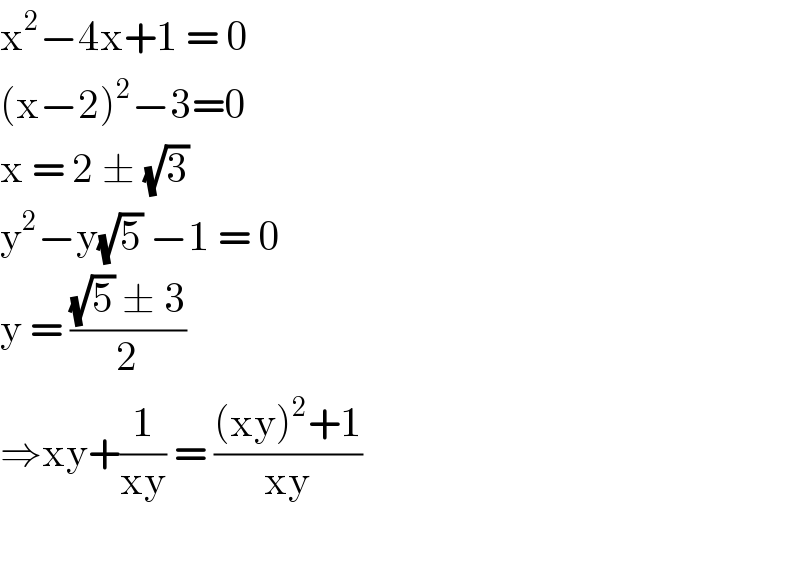
$$\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{1}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{x}\:=\:\mathrm{2}\:\pm\:\sqrt{\mathrm{3}}\: \\ $$$$\mathrm{y}^{\mathrm{2}} −\mathrm{y}\sqrt{\mathrm{5}}\:−\mathrm{1}\:=\:\mathrm{0} \\ $$$$\mathrm{y}\:=\:\frac{\sqrt{\mathrm{5}}\:\pm\:\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{xy}+\frac{\mathrm{1}}{\mathrm{xy}}\:=\:\frac{\left(\mathrm{xy}\right)^{\mathrm{2}} +\mathrm{1}}{\mathrm{xy}} \\ $$$$ \\ $$
Commented by TawaTawa1 last updated on 09/Apr/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by $@ty@m123 last updated on 07/Apr/20
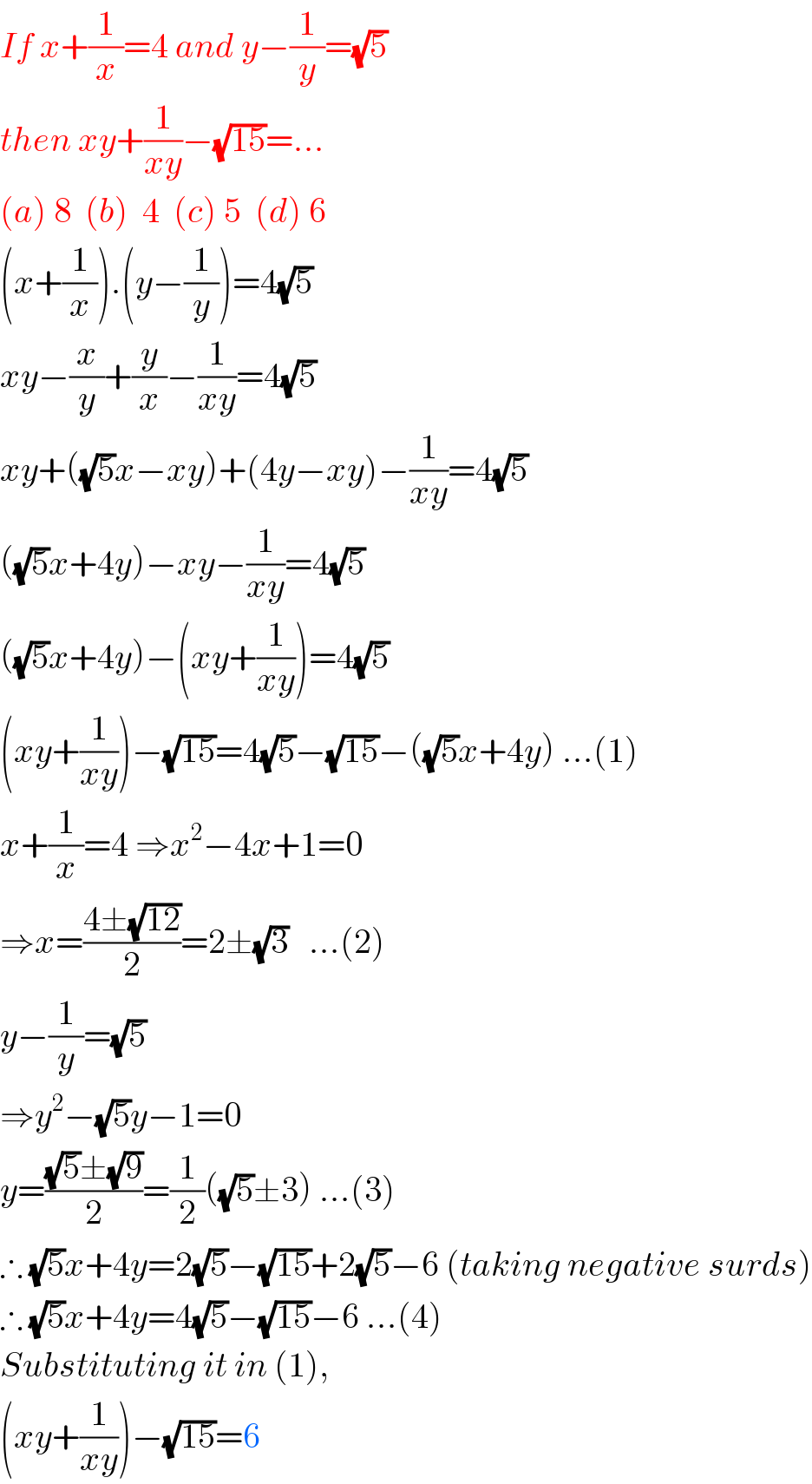
$${If}\:{x}+\frac{\mathrm{1}}{{x}}=\mathrm{4}\:{and}\:{y}−\frac{\mathrm{1}}{{y}}=\sqrt{\mathrm{5}} \\ $$$${then}\:{xy}+\frac{\mathrm{1}}{{xy}}−\sqrt{\mathrm{15}}=… \\ $$$$\left({a}\right)\:\mathrm{8}\:\:\left({b}\right)\:\:\mathrm{4}\:\:\left({c}\right)\:\mathrm{5}\:\:\left({d}\right)\:\mathrm{6} \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}}\right).\left({y}−\frac{\mathrm{1}}{{y}}\right)=\mathrm{4}\sqrt{\mathrm{5}} \\ $$$${xy}−\frac{{x}}{{y}}+\frac{{y}}{{x}}−\frac{\mathrm{1}}{{xy}}=\mathrm{4}\sqrt{\mathrm{5}} \\ $$$${xy}+\left(\sqrt{\mathrm{5}}{x}−{xy}\right)+\left(\mathrm{4}{y}−{xy}\right)−\frac{\mathrm{1}}{{xy}}=\mathrm{4}\sqrt{\mathrm{5}} \\ $$$$\left(\sqrt{\mathrm{5}}{x}+\mathrm{4}{y}\right)−{xy}−\frac{\mathrm{1}}{{xy}}=\mathrm{4}\sqrt{\mathrm{5}} \\ $$$$\left(\sqrt{\mathrm{5}}{x}+\mathrm{4}{y}\right)−\left({xy}+\frac{\mathrm{1}}{{xy}}\right)=\mathrm{4}\sqrt{\mathrm{5}} \\ $$$$\left({xy}+\frac{\mathrm{1}}{{xy}}\right)−\sqrt{\mathrm{15}}=\mathrm{4}\sqrt{\mathrm{5}}−\sqrt{\mathrm{15}}−\left(\sqrt{\mathrm{5}}{x}+\mathrm{4}{y}\right)\:…\left(\mathrm{1}\right) \\ $$$${x}+\frac{\mathrm{1}}{{x}}=\mathrm{4}\:\Rightarrow{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{4}\pm\sqrt{\mathrm{12}}}{\mathrm{2}}=\mathrm{2}\pm\sqrt{\mathrm{3}}\:\:\:…\left(\mathrm{2}\right) \\ $$$${y}−\frac{\mathrm{1}}{{y}}=\sqrt{\mathrm{5}} \\ $$$$\Rightarrow{y}^{\mathrm{2}} −\sqrt{\mathrm{5}}{y}−\mathrm{1}=\mathrm{0} \\ $$$${y}=\frac{\sqrt{\mathrm{5}}\pm\sqrt{\mathrm{9}}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{5}}\pm\mathrm{3}\right)\:…\left(\mathrm{3}\right) \\ $$$$\therefore\:\sqrt{\mathrm{5}}{x}+\mathrm{4}{y}=\mathrm{2}\sqrt{\mathrm{5}}−\sqrt{\mathrm{15}}+\mathrm{2}\sqrt{\mathrm{5}}−\mathrm{6}\:\left({taking}\:{negative}\:{surds}\right) \\ $$$$\therefore\:\sqrt{\mathrm{5}}{x}+\mathrm{4}{y}=\mathrm{4}\sqrt{\mathrm{5}}−\sqrt{\mathrm{15}}−\mathrm{6}\:…\left(\mathrm{4}\right) \\ $$$${Substituting}\:{it}\:{in}\:\left(\mathrm{1}\right), \\ $$$$\left({xy}+\frac{\mathrm{1}}{{xy}}\right)−\sqrt{\mathrm{15}}=\mathrm{6} \\ $$
Commented by TawaTawa1 last updated on 07/Apr/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
