Question Number 87975 by ajfour last updated on 07/Apr/20
Commented by ajfour last updated on 07/Apr/20
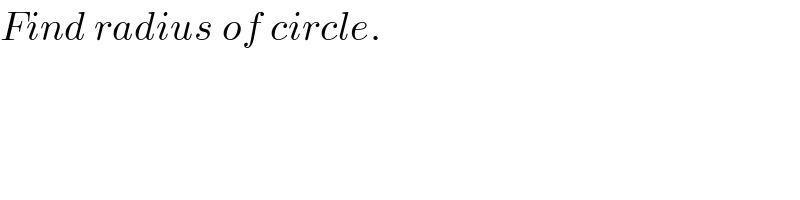
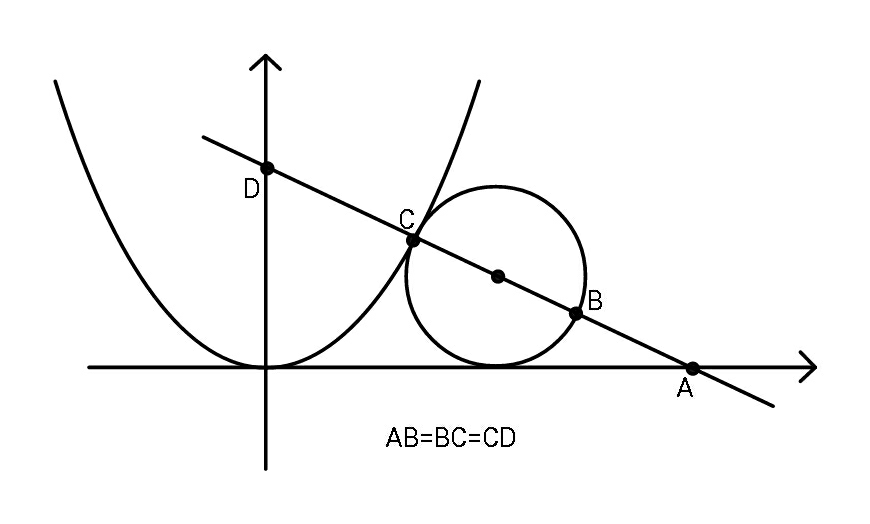
$${Find}\:{radius}\:{of}\:{circle}. \\ $$
Commented by Tony Lin last updated on 07/Apr/20
Commented by Tony Lin last updated on 07/Apr/20

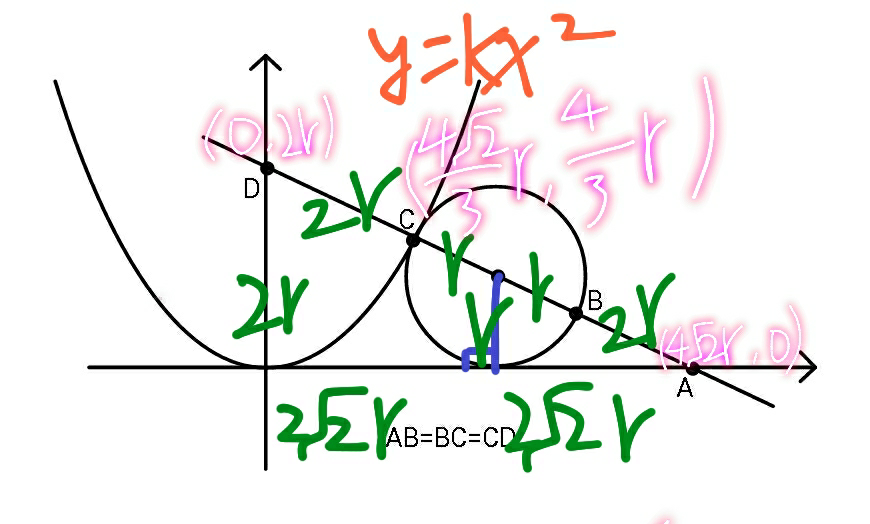
$$\frac{\mathrm{4}}{\mathrm{3}}{r}={k}\left(\frac{\mathrm{4}\sqrt{\mathrm{2}}}{\mathrm{3}}{r}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{r}=\frac{\mathrm{3}}{\mathrm{8}{k}} \\ $$
Commented by Tony Lin last updated on 07/Apr/20
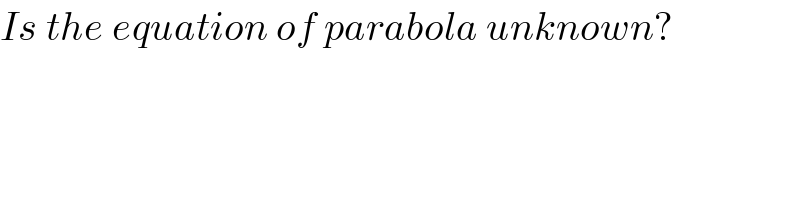
$${Is}\:{the}\:{equation}\:{of}\:{parabola}\:{unknown}? \\ $$
Commented by ajfour last updated on 07/Apr/20
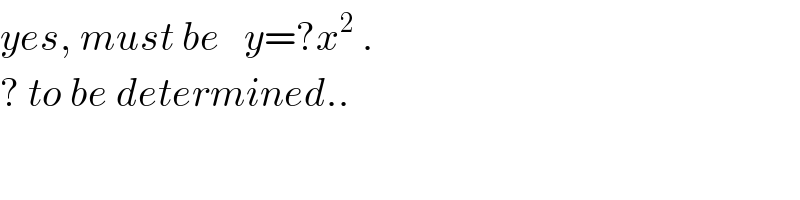
$${yes},\:{must}\:{be}\:\:\:{y}=?{x}^{\mathrm{2}} \:. \\ $$$$?\:{to}\:{be}\:{determined}.. \\ $$
Commented by ajfour last updated on 07/Apr/20

$${I}\:{got}\:{kr}=\frac{\mathrm{3}}{\mathrm{4}}\:,\:{and}\:{there}\:{seems} \\ $$$$\left({to}\:{me}\:{now}\right),\:{that}\:{something}'{s} \\ $$$${wrong}\:{with}\:{this}\:{question}\:\left({i}\:{thought}\right. \\ $$$$\left.{of}\:{myself}..\right) \\ $$
Commented by Tony Lin last updated on 07/Apr/20
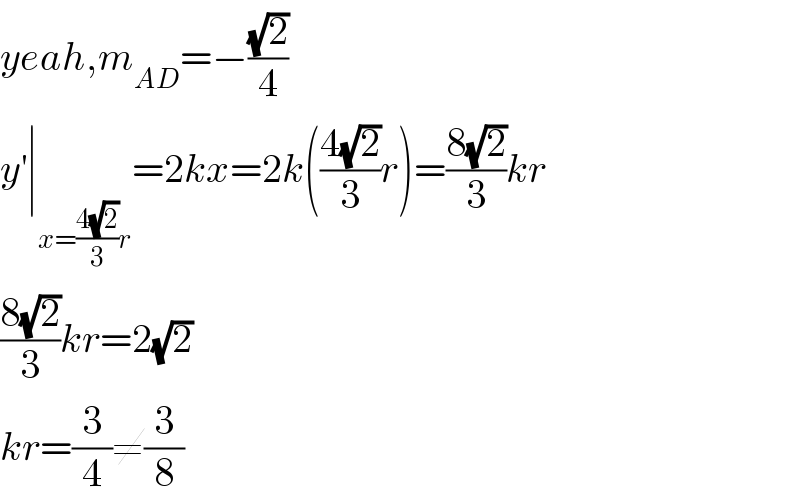
$${yeah},{m}_{{AD}} =−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$$${y}^{'} \mid_{{x}=\frac{\mathrm{4}\sqrt{\mathrm{2}}}{\mathrm{3}}{r}} =\mathrm{2}{kx}=\mathrm{2}{k}\left(\frac{\mathrm{4}\sqrt{\mathrm{2}}}{\mathrm{3}}{r}\right)=\frac{\mathrm{8}\sqrt{\mathrm{2}}}{\mathrm{3}}{kr} \\ $$$$\frac{\mathrm{8}\sqrt{\mathrm{2}}}{\mathrm{3}}{kr}=\mathrm{2}\sqrt{\mathrm{2}} \\ $$$${kr}=\frac{\mathrm{3}}{\mathrm{4}}\neq\frac{\mathrm{3}}{\mathrm{8}} \\ $$
