Menu Close

Question-87991

Tinku Tara 0 Comments
Pin




Question Number 87991 by necxxx last updated on 07/Apr/20
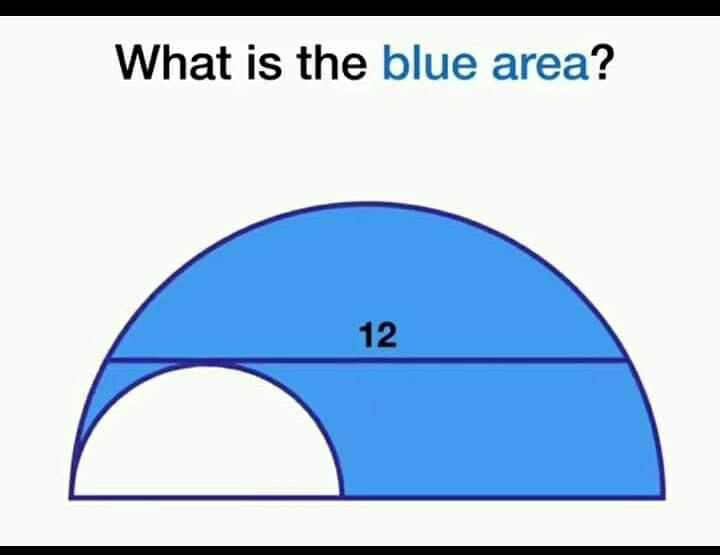
Commented by necxxx last updated on 07/Apr/20
please help
$${please}\:{help} \\ $$
Answered by mr W last updated on 07/Apr/20
R=radius of big semicircle r=radius of small semicircle b=length of chord R^2 −r^2 =((b/2))^2 (π/2)R^2 −(π/2)r^2 =((b^2 π)/8) big−small semicircle=((b^2 π)/8) blue area=((b^2 π)/8)=((12^2 π)/8)=18π
$${R}={radius}\:{of}\:{big}\:{semicircle} \\ $$$${r}={radius}\:{of}\:{small}\:{semicircle} \\ $$$${b}={length}\:{of}\:{chord} \\ $$$${R}^{\mathrm{2}} −{r}^{\mathrm{2}} =\left(\frac{{b}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\frac{\pi}{\mathrm{2}}{R}^{\mathrm{2}} −\frac{\pi}{\mathrm{2}}{r}^{\mathrm{2}} =\frac{{b}^{\mathrm{2}} \pi}{\mathrm{8}} \\ $$$${big}−{small}\:{semicircle}=\frac{{b}^{\mathrm{2}} \pi}{\mathrm{8}} \\ $$$${blue}\:{area}=\frac{{b}^{\mathrm{2}} \pi}{\mathrm{8}}=\frac{\mathrm{12}^{\mathrm{2}} \pi}{\mathrm{8}}=\mathrm{18}\pi \\ $$
Commented by necxxx last updated on 07/Apr/20
wow.. what an eye opener. Thank you sir
$${wow}..\:{what}\:{an}\:{eye}\:{opener}.\:{Thank}\:{you} \\ $$$${sir} \\ $$
Commented by necxxx last updated on 07/Apr/20
please sir I just tried to understanx that formula you used and I′m stuck. how is the area of the blue region= (((12^2 )/8_ )π) ?
$${please}\:{sir}\:{I}\:{just}\:{tried}\:{to}\:{understanx}\:{that} \\ $$$${formula}\:{you}\:{used}\:{and}\:{I}'{m}\:{stuck}. \\ $$$$ \\ $$$${how}\:{is}\:{the}\:{area}\:{of}\:{the}\:{blue}\:{region}=\:\left(\frac{\mathrm{12}^{\mathrm{2}} }{\mathrm{8}_{} }\pi\right)\:\:? \\ $$
Commented by mr W last updated on 07/Apr/20
blue area=big semicircle − small semicircle big semicircle=((πR^2 )/2) as all earth people know small semicircle=((πr^2 )/2) as all earth people know ⇒blue area=((πR^2 )/2)−((πr^2 )/2) since (π/2)R^2 −(π/2)r^2 =((b^2 π)/8) as proved ⇒blue area=((b^2 π)/8) since b=12 as given ⇒blue area=((12^2 π)/8)=18π
$${blue}\:{area}={big}\:{semicircle}\:−\:{small}\:{semicircle} \\ $$$$ \\ $$$${big}\:{semicircle}=\frac{\pi{R}^{\mathrm{2}} }{\mathrm{2}}\:{as}\:{all}\:{earth}\:{people}\:{know} \\ $$$${small}\:{semicircle}=\frac{\pi{r}^{\mathrm{2}} }{\mathrm{2}}\:{as}\:{all}\:{earth}\:{people}\:{know} \\ $$$$\Rightarrow{blue}\:{area}=\frac{\pi{R}^{\mathrm{2}} }{\mathrm{2}}−\frac{\pi{r}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$ \\ $$$${since}\:\frac{\pi}{\mathrm{2}}{R}^{\mathrm{2}} −\frac{\pi}{\mathrm{2}}{r}^{\mathrm{2}} =\frac{{b}^{\mathrm{2}} \pi}{\mathrm{8}}\:{as}\:{proved} \\ $$$$\Rightarrow{blue}\:{area}=\frac{{b}^{\mathrm{2}} \pi}{\mathrm{8}} \\ $$$$ \\ $$$${since}\:{b}=\mathrm{12}\:{as}\:{given} \\ $$$$\Rightarrow{blue}\:{area}=\frac{\mathrm{12}^{\mathrm{2}} \pi}{\mathrm{8}}=\mathrm{18}\pi \\ $$
Commented by $@ty@m123 last updated on 07/Apr/20
Wonnderful!
$${Wonnderful}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *