Question Number 88021 by naka3546 last updated on 07/Apr/20
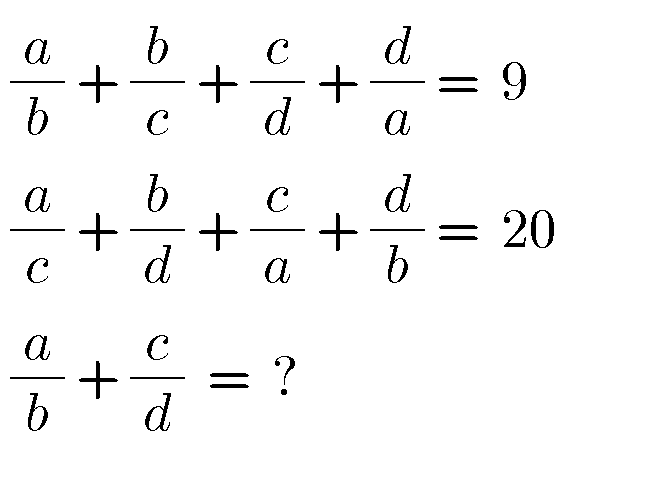
Commented by MJS last updated on 07/Apr/20
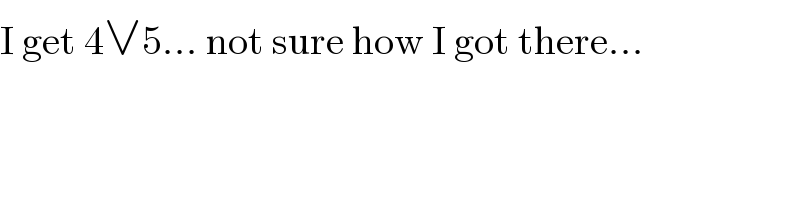
$$\mathrm{I}\:\mathrm{get}\:\mathrm{4}\vee\mathrm{5}…\:\mathrm{not}\:\mathrm{sure}\:\mathrm{how}\:\mathrm{I}\:\mathrm{got}\:\mathrm{there}… \\ $$
Commented by naka3546 last updated on 08/Apr/20
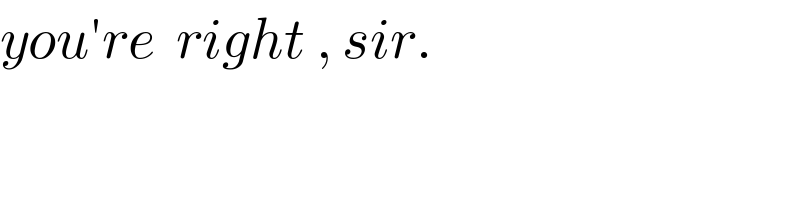
$${you}'{re}\:\:{right}\:,\:{sir}. \\ $$
Answered by $@ty@m123 last updated on 08/Apr/20
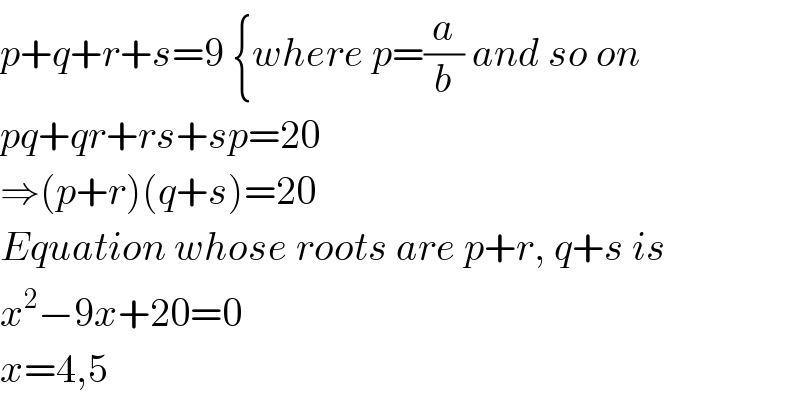
$${p}+{q}+{r}+{s}=\mathrm{9}\:\left\{{where}\:{p}=\frac{{a}}{{b}}\:{and}\:{so}\:{on}\right. \\ $$$${pq}+{qr}+{rs}+{sp}=\mathrm{20} \\ $$$$\Rightarrow\left({p}+{r}\right)\left({q}+{s}\right)=\mathrm{20} \\ $$$${Equation}\:{whose}\:{roots}\:{are}\:{p}+{r},\:{q}+{s}\:{is} \\ $$$${x}^{\mathrm{2}} −\mathrm{9}{x}+\mathrm{20}=\mathrm{0} \\ $$$${x}=\mathrm{4},\mathrm{5} \\ $$
Commented by Prithwish Sen 1 last updated on 08/Apr/20

$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{will}\:\mathrm{be} \\ $$$$\left(\mathrm{p}+\mathrm{r}\right)\left(\mathrm{q}+\mathrm{s}\right)=\mathrm{20} \\ $$
Commented by $@ty@m123 last updated on 08/Apr/20
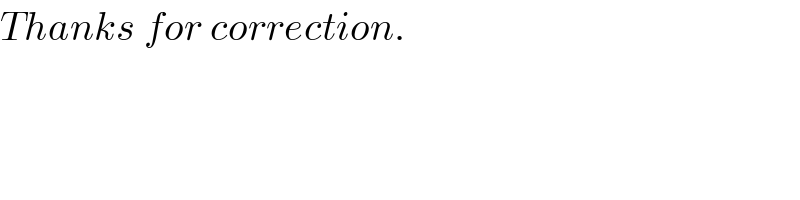
$${Thanks}\:{for}\:{correction}. \\ $$
