Question Number 88029 by M±th+et£s last updated on 07/Apr/20
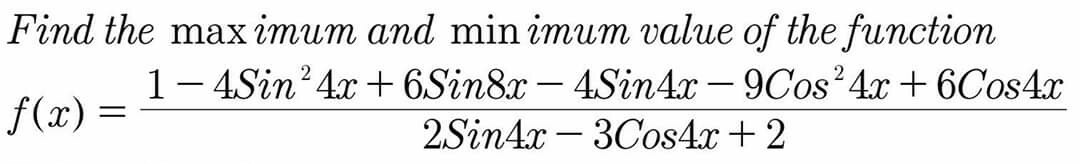
Answered by mind is power last updated on 08/Apr/20

$$−\mathrm{4}{sin}^{\mathrm{2}} \left(\mathrm{4}{x}\right)−\mathrm{8}{sin}\left(\mathrm{4}{x}\right)−\mathrm{9}{cos}^{\mathrm{2}} \left(\mathrm{4}{x}\right)+\mathrm{12}{cos}\left(\mathrm{4}{x}\right)−\mathrm{4}+\mathrm{6}{sin}\left(\mathrm{8}{x}\right) \\ $$$$=−\left(\mathrm{2}{sin}\left(\mathrm{4}{x}\right)−\mathrm{3}{cos}\left(\mathrm{4}{x}\right)+\mathrm{2}\right)^{\mathrm{2}} \\ $$$${f}\left({x}\right)=\frac{−\left(\mathrm{2}{sin}\left(\mathrm{4}{x}\right)−\mathrm{3}{cos}\left(\mathrm{4}{x}\right)+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{1}+\mathrm{4}−\mathrm{6}{cos}\left(\mathrm{4}{x}\right)+\mathrm{4}{sin}\left(\mathrm{4}{x}\right)}{\mathrm{2}{sin}\left(\mathrm{4}{x}\right)−\mathrm{3}{cos}\left(\mathrm{4}{x}\right)+\mathrm{2}} \\ $$$${let}\:{Y}\left({x}\right)=\mathrm{2}{sin}\left(\mathrm{4}{x}\right)−\mathrm{3}{cos}\left(\mathrm{4}{x}\right)+\mathrm{2} \\ $$$${g}\left({y}\right)=−{Y}+\frac{\mathrm{1}}{{Y}}+\mathrm{2} \\ $$$${g}'\left({y}\right)=−\mathrm{1}−\frac{\mathrm{1}}{{y}^{\mathrm{2}} } \\ $$$${y}\left({x}+\frac{\pi}{\mathrm{2}}\right)={y}\left({x}\right) \\ $$$$\mathrm{2}{sin}\left(\mathrm{4}{x}\right)−\mathrm{3}{cos}\left(\mathrm{4}{x}\right)+\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\sqrt{\mathrm{13}}{sin}\left(\mathrm{4}{x}−{arcsin}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{13}}}\right)\right)+\mathrm{2}=\mathrm{0} \\ $$$${has}\:{solution}\:\:{min}\:{and}\:{max}\:{didnt}\:{existe} \\ $$$$ \\ $$$$ \\ $$
Commented by M±th+et£s last updated on 08/Apr/20

$${god}\:{bless}\:{you}\:{sir} \\ $$
