Question Number 88050 by Sahil vampire last updated on 08/Apr/20

Commented by mr W last updated on 08/Apr/20
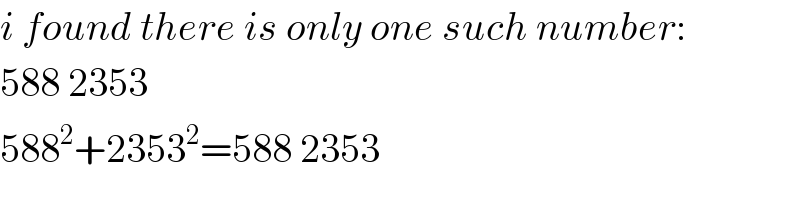
$${i}\:{found}\:{there}\:{is}\:{only}\:{one}\:{such}\:{number}: \\ $$$$\mathrm{588}\:\mathrm{2353} \\ $$$$\mathrm{588}^{\mathrm{2}} +\mathrm{2353}^{\mathrm{2}} =\mathrm{588}\:\mathrm{2353} \\ $$
Commented by Sahil vampire last updated on 08/Apr/20
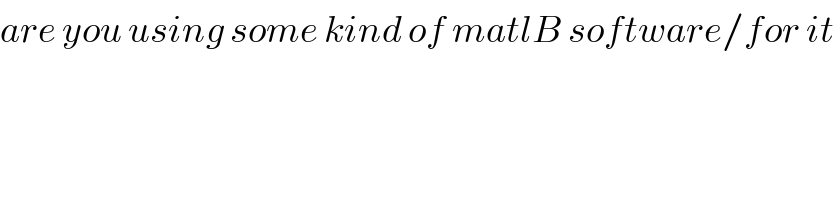
$${are}\:{you}\:{using}\:{some}\:{kind}\:{of}\:{matlB}\:{software}/{for}\:{it} \\ $$
Commented by mr W last updated on 08/Apr/20
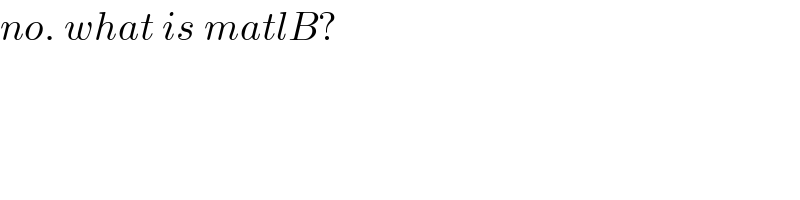
$${no}.\:{what}\:{is}\:{matlB}? \\ $$
Commented by Sahil vampire last updated on 08/Apr/20
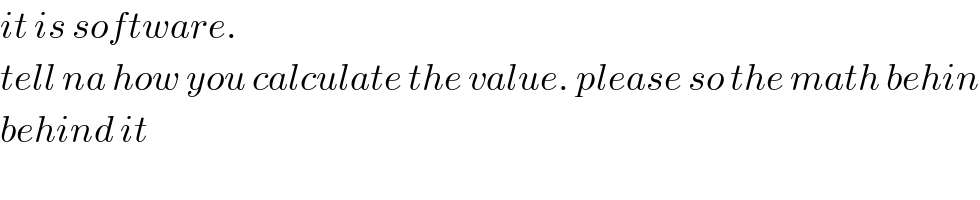
$${it}\:{is}\:{software}. \\ $$$${tell}\:{na}\:{how}\:{you}\:{calculate}\:{the}\:{value}.\:{please}\:{so}\:{the}\:{math}\:{behin} \\ $$$${behind}\:{it} \\ $$
Commented by mr W last updated on 08/Apr/20
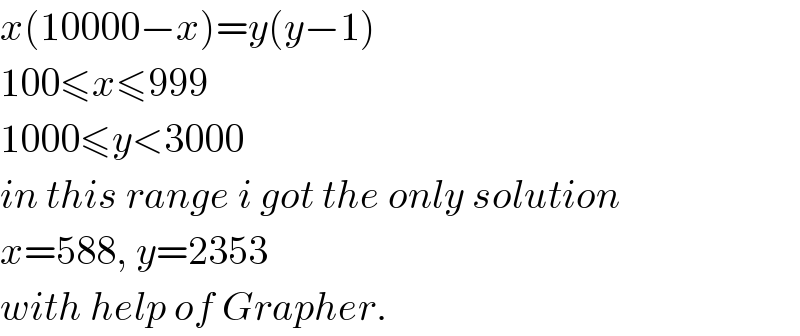
$${x}\left(\mathrm{10000}−{x}\right)={y}\left({y}−\mathrm{1}\right) \\ $$$$\mathrm{100}\leqslant{x}\leqslant\mathrm{999} \\ $$$$\mathrm{1000}\leqslant{y}<\mathrm{3000} \\ $$$${in}\:{this}\:{range}\:{i}\:{got}\:{the}\:{only}\:{solution} \\ $$$${x}=\mathrm{588},\:{y}=\mathrm{2353} \\ $$$${with}\:{help}\:{of}\:{Grapher}. \\ $$
Commented by Sahil vampire last updated on 08/Apr/20
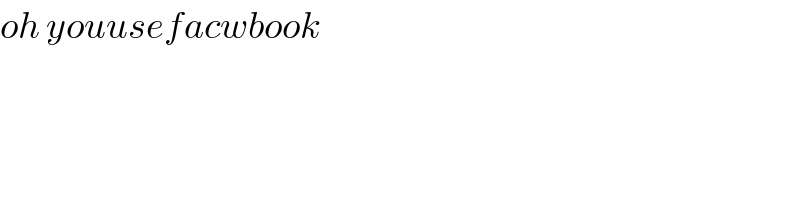
$${oh}\:{youusefacwbook} \\ $$
Answered by Rasheed.Sindhi last updated on 08/Apr/20

$${Let}\:{the}\:{number}\:{is}\:\mathrm{abcdefg}. \\ $$$$\left(\mathrm{10}^{\mathrm{2}} \mathrm{a}+\mathrm{10b}+\mathrm{c}\right)^{\mathrm{2}} +\left(\mathrm{10}^{\mathrm{3}} \mathrm{d}+\mathrm{10}^{\mathrm{2}} \mathrm{e}+\mathrm{10f}+\mathrm{g}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:=\mathrm{10}^{\mathrm{6}} \mathrm{a}+\mathrm{10}^{\mathrm{5}} \mathrm{b}+\mathrm{10}^{\mathrm{4}} \mathrm{c}+\mathrm{10}^{\mathrm{3}} \mathrm{d}+\mathrm{10}^{\mathrm{2}} \mathrm{e}+\mathrm{10f}+\mathrm{g} \\ $$$${The}\:{term}\:{containing}\:\mathrm{10}^{\mathrm{6}} \:{in}\:{lhs}: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{is}\:{equal}\:{to} \\ $$$${The}\:{term}\:{containing}\:\mathrm{10}^{\mathrm{6}} \:{in}\:{rhs}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{a} \\ $$$$\:\:\:\:\:\mathbb{WRONG}\:\mathbb{IDEA} \\ $$
Commented by mr W last updated on 08/Apr/20

$${say}\:{the}\:{number}\:{is}\:\mathrm{abcdefg}. \\ $$$${say}\:{x}=\mathrm{abc} \\ $$$${say}\:{y}=\mathrm{defg} \\ $$$$\mathrm{100}\leqslant{x}\leqslant\mathrm{999} \\ $$$$\mathrm{1000}\leqslant{y}\leqslant\mathrm{9999} \\ $$$${given}:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{10000}{x}+{y} \\ $$$$\Rightarrow{x}\left(\mathrm{10000}−{x}\right)={y}\left({y}−\mathrm{1}\right) \\ $$$$…… \\ $$
