Question-88068

Question Number 88068 by student work last updated on 08/Apr/20

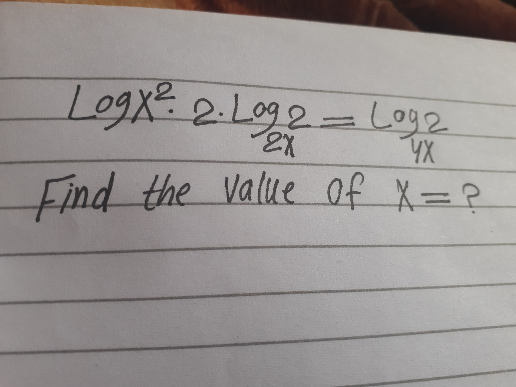
Commented by john santu last updated on 08/Apr/20

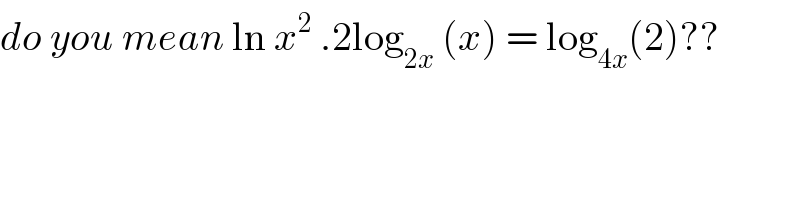
do you mean ln x^2 .2log_(2x) (x) = log_(4x) (2)??

$${do}\:{you}\:{mean}\:\mathrm{ln}\:{x}^{\mathrm{2}} \:.\mathrm{2log}_{\mathrm{2}{x}} \:\left({x}\right)\:=\:\mathrm{log}_{\mathrm{4}{x}} \left(\mathrm{2}\right)?? \\ $$

Commented by $@ty@m123 last updated on 08/Apr/20

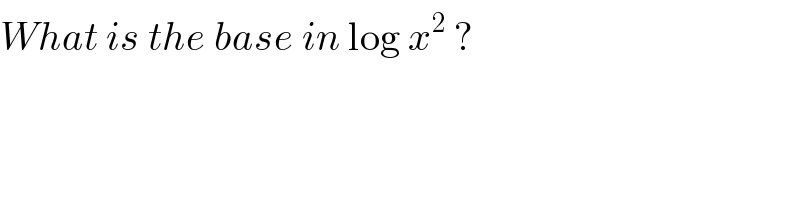
$${What}\:{is}\:{the}\:{base}\:{in}\:\mathrm{log}\:{x}^{\mathrm{2}} \:? \\ $$

Commented by john santu last updated on 08/Apr/20

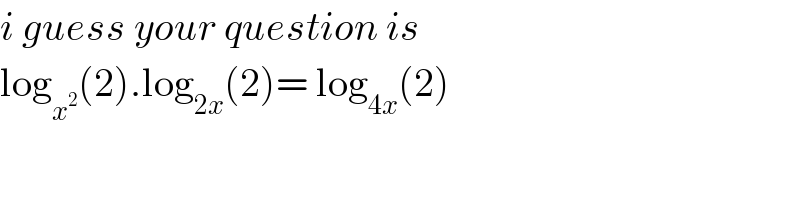
i guess your question is log_x^2 (2).log_(2x) (2)= log_(4x) (2)

$${i}\:{guess}\:{your}\:{question}\:{is}\: \\ $$$$\mathrm{log}_{{x}^{\mathrm{2}} } \left(\mathrm{2}\right).\mathrm{log}_{\mathrm{2}{x}} \left(\mathrm{2}\right)=\:\mathrm{log}_{\mathrm{4}{x}} \left(\mathrm{2}\right)\: \\ $$

Answered by MJS last updated on 08/Apr/20

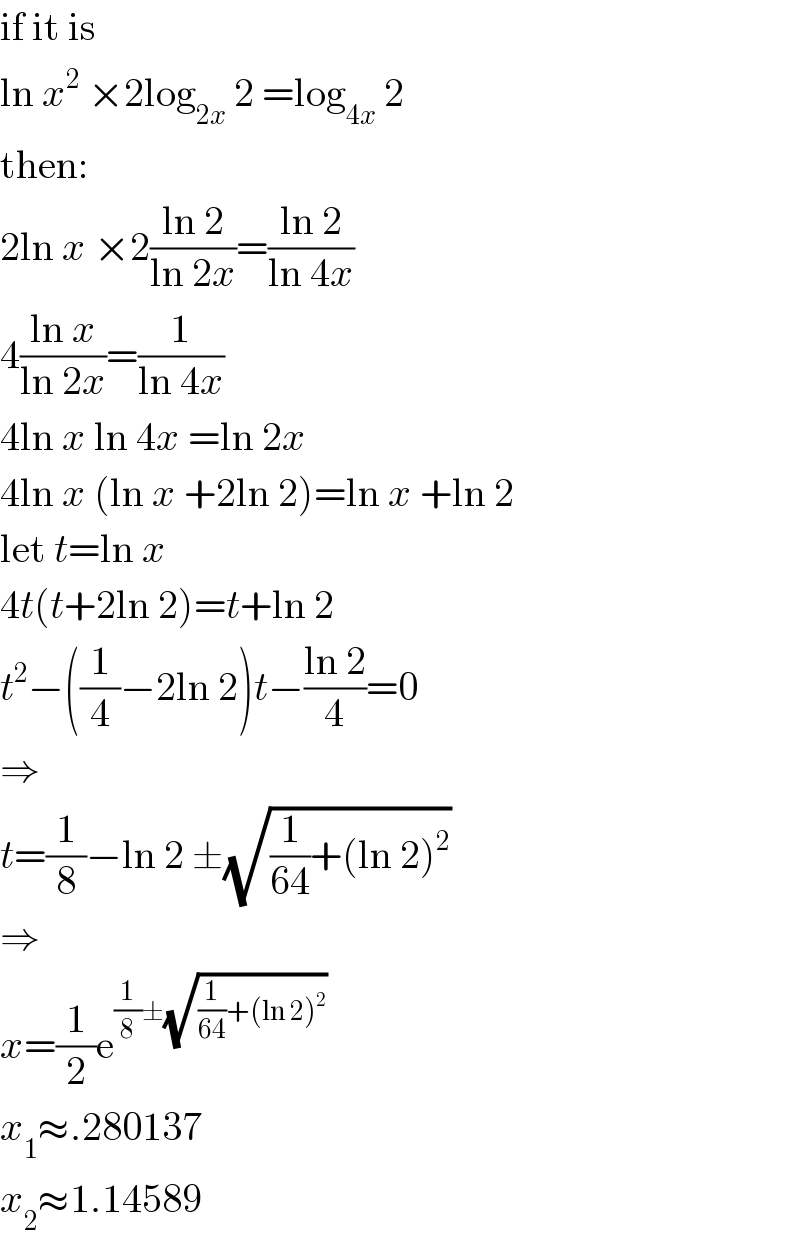
if it is ln x^2 ×2log_(2x) 2 =log_(4x) 2 then: 2ln x ×2((ln 2)/(ln 2x))=((ln 2)/(ln 4x)) 4((ln x)/(ln 2x))=(1/(ln 4x)) 4ln x ln 4x =ln 2x 4ln x (ln x +2ln 2)=ln x +ln 2 let t=ln x 4t(t+2ln 2)=t+ln 2 t^2 −((1/4)−2ln 2)t−((ln 2)/4)=0 ⇒ t=(1/8)−ln 2 ±(√((1/(64))+(ln 2)^2 )) ⇒ x=(1/2)e^((1/8)±(√((1/(64))+(ln 2)^2 ))) x_1 ≈.280137 x_2 ≈1.14589

$$\mathrm{if}\:\mathrm{it}\:\mathrm{is} \\ $$$$\mathrm{ln}\:{x}^{\mathrm{2}} \:×\mathrm{2log}_{\mathrm{2}{x}} \:\mathrm{2}\:=\mathrm{log}_{\mathrm{4}{x}} \:\mathrm{2} \\ $$$$\mathrm{then}: \\ $$$$\mathrm{2ln}\:{x}\:×\mathrm{2}\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{ln}\:\mathrm{2}{x}}=\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{ln}\:\mathrm{4}{x}} \\ $$$$\mathrm{4}\frac{\mathrm{ln}\:{x}}{\mathrm{ln}\:\mathrm{2}{x}}=\frac{\mathrm{1}}{\mathrm{ln}\:\mathrm{4}{x}} \\ $$$$\mathrm{4ln}\:{x}\:\mathrm{ln}\:\mathrm{4}{x}\:=\mathrm{ln}\:\mathrm{2}{x} \\ $$$$\mathrm{4ln}\:{x}\:\left(\mathrm{ln}\:{x}\:+\mathrm{2ln}\:\mathrm{2}\right)=\mathrm{ln}\:{x}\:+\mathrm{ln}\:\mathrm{2} \\ $$$$\mathrm{let}\:{t}=\mathrm{ln}\:{x} \\ $$$$\mathrm{4}{t}\left({t}+\mathrm{2ln}\:\mathrm{2}\right)={t}+\mathrm{ln}\:\mathrm{2} \\ $$$${t}^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{2ln}\:\mathrm{2}\right){t}−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${t}=\frac{\mathrm{1}}{\mathrm{8}}−\mathrm{ln}\:\mathrm{2}\:\pm\sqrt{\frac{\mathrm{1}}{\mathrm{64}}+\left(\mathrm{ln}\:\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{8}}\pm\sqrt{\frac{\mathrm{1}}{\mathrm{64}}+\left(\mathrm{ln}\:\mathrm{2}\right)^{\mathrm{2}} }} \\ $$$${x}_{\mathrm{1}} \approx.\mathrm{280137} \\ $$$${x}_{\mathrm{2}} \approx\mathrm{1}.\mathrm{14589} \\ $$

Commented by Zainal Arifin last updated on 13/Apr/20

$$\mathrm{thank}\:\mathrm{sir} \\ $$

Answered by MJS last updated on 08/Apr/20

if it is log_x^2 2 ×log_(2x) 2 =log_(4x) 2 then ((ln 2)/(ln x^2 ))×((ln 2)/(ln 2x))=((ln 2)/(ln 4x)) ((ln 2)/(2ln x (ln x +ln 2)))=(1/(ln 4x)) ...let t=ln x t^2 +((ln 2)/2)t−(ln 2)^2 =0 ⇒ t=−((1±(√(17)))/4)ln 2 ⇒ x=(1/2)2^((3±(√(17)))/4) x_1 ≈.411574 x_2 ≈1.71806

$$\mathrm{if}\:\mathrm{it}\:\mathrm{is} \\ $$$$\mathrm{log}_{{x}^{\mathrm{2}} } \:\mathrm{2}\:×\mathrm{log}_{\mathrm{2}{x}} \:\mathrm{2}\:=\mathrm{log}_{\mathrm{4}{x}} \:\mathrm{2} \\ $$$$\mathrm{then} \\ $$$$\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{ln}\:{x}^{\mathrm{2}} }×\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{ln}\:\mathrm{2}{x}}=\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{ln}\:\mathrm{4}{x}} \\ $$$$\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2ln}\:{x}\:\left(\mathrm{ln}\:{x}\:+\mathrm{ln}\:\mathrm{2}\right)}=\frac{\mathrm{1}}{\mathrm{ln}\:\mathrm{4}{x}} \\ $$$$…\mathrm{let}\:{t}=\mathrm{ln}\:{x} \\ $$$${t}^{\mathrm{2}} +\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}{t}−\left(\mathrm{ln}\:\mathrm{2}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:{t}=−\frac{\mathrm{1}\pm\sqrt{\mathrm{17}}}{\mathrm{4}}\mathrm{ln}\:\mathrm{2} \\ $$$$\Rightarrow\:{x}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{2}^{\frac{\mathrm{3}\pm\sqrt{\mathrm{17}}}{\mathrm{4}}} \\ $$$${x}_{\mathrm{1}} \approx.\mathrm{411574} \\ $$$${x}_{\mathrm{2}} \approx\mathrm{1}.\mathrm{71806} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply