Question Number 88069 by Power last updated on 08/Apr/20
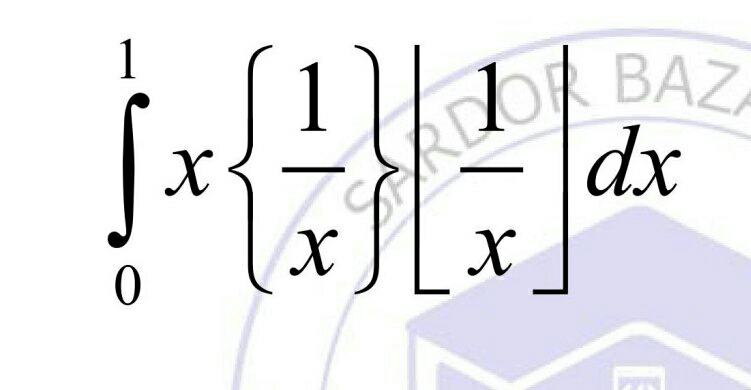
Commented by Power last updated on 08/Apr/20
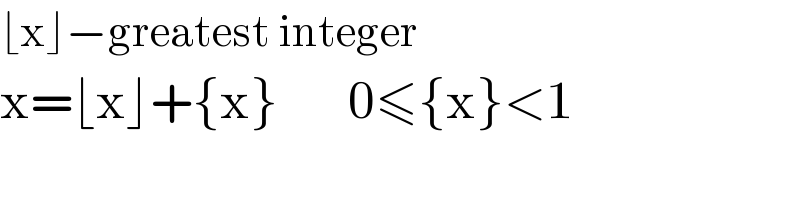
$$\lfloor\mathrm{x}\rfloor−\mathrm{greatest}\:\mathrm{integer}\: \\ $$$$\mathrm{x}=\lfloor\mathrm{x}\rfloor+\left\{\mathrm{x}\right\}\:\:\:\:\:\:\:\mathrm{0}\leqslant\left\{\mathrm{x}\right\}<\mathrm{1} \\ $$
Commented by mathmax by abdo last updated on 08/Apr/20
![A =∫_0 ^1 x{(1/x)}[(1/x)]dx we have (1/x)=[(1/x)]+{(1/x)} ⇒ A =∫_0 ^1 x((1/x)−[(1/x)])[(1/x)]dx =∫_0 ^1 (1−x[(1/x)])[(1/x)]dx we do the changement (1/x) =t ⇒ A =−∫_1 ^(+∞) (1−(1/t)[t])[t] (−(dt/t^2 )) =∫_1 ^(+∞) ((1/t^2 )−(([t]^2 )/t^3 ))dt =∫_1 ^(+∞ ) (dt/t^2 )−∫_1 ^(+∞) (([t]^2 )/t^3 )dt but we have ∫_1 ^(+∞) (dt/t^2 ) =[−(1/t)]_1 ^(+∞) =1 ∫_1 ^(+∞) (([t]^2 )/t^3 )dt =Σ_(n=1) ^∞ ∫_n ^(n+1) (n^2 /t^3 )dt =Σ_(n=1) ^∞ n^2 ∫_n ^(n+1) t^(−3) dt =Σ_(n=1) ^∞ n^2 [−(1/2)t^(−2) ]_n ^(n+1) =−(1/2)Σ_(n=1) ^∞ n^2 {(1/((n+1)^2 ))−(1/n^2 )} =−(1/2)Σ_(n=1) ^∞ ((n^2 /((n+1)^2 ))−1) =−(1/2)Σ_(n=1) ^∞ (((n^2 −(n^2 +2n+1))/((n+1)^2 ))) =−(1/2) Σ_(n=1) ^∞ ((−2n−1)/((n+1)^2 )) =Σ_(n=1) ^∞ ((2n+1)/(2(n+1)^2 )) and this serie is divergente because ((2n+1)/(2(n+1)^2 )) ∼(1/n)( n∼+∞)](https://www.tinkutara.com/question/Q88154.png)
$${A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}\left\{\frac{\mathrm{1}}{{x}}\right\}\left[\frac{\mathrm{1}}{{x}}\right]{dx}\:\:{we}\:{have}\:\frac{\mathrm{1}}{{x}}=\left[\frac{\mathrm{1}}{{x}}\right]+\left\{\frac{\mathrm{1}}{{x}}\right\}\:\Rightarrow \\ $$$${A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} {x}\left(\frac{\mathrm{1}}{{x}}−\left[\frac{\mathrm{1}}{{x}}\right]\right)\left[\frac{\mathrm{1}}{{x}}\right]{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}\left[\frac{\mathrm{1}}{{x}}\right]\right)\left[\frac{\mathrm{1}}{{x}}\right]{dx}\:\:{we}\:{do}\:{the}\:{changement} \\ $$$$\frac{\mathrm{1}}{{x}}\:={t}\:\Rightarrow\:{A}\:=−\int_{\mathrm{1}} ^{+\infty} \left(\mathrm{1}−\frac{\mathrm{1}}{{t}}\left[{t}\right]\right)\left[{t}\right]\:\left(−\frac{{dt}}{{t}^{\mathrm{2}} }\right) \\ $$$$=\int_{\mathrm{1}} ^{+\infty} \:\left(\frac{\mathrm{1}}{{t}^{\mathrm{2}} }−\frac{\left[{t}\right]^{\mathrm{2}} }{{t}^{\mathrm{3}} }\right){dt}\:=\int_{\mathrm{1}} ^{+\infty\:} \frac{{dt}}{{t}^{\mathrm{2}} }−\int_{\mathrm{1}} ^{+\infty} \:\frac{\left[{t}\right]^{\mathrm{2}} }{{t}^{\mathrm{3}} }{dt}\:\:{but}\:{we}\:{have} \\ $$$$\int_{\mathrm{1}} ^{+\infty} \:\frac{{dt}}{{t}^{\mathrm{2}} }\:=\left[−\frac{\mathrm{1}}{{t}}\right]_{\mathrm{1}} ^{+\infty} =\mathrm{1} \\ $$$$\int_{\mathrm{1}} ^{+\infty} \:\frac{\left[{t}\right]^{\mathrm{2}} }{{t}^{\mathrm{3}} }{dt}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\int_{{n}} ^{{n}+\mathrm{1}} \:\frac{{n}^{\mathrm{2}} }{{t}^{\mathrm{3}} }{dt}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:{n}^{\mathrm{2}} \:\int_{{n}} ^{{n}+\mathrm{1}} \:{t}^{−\mathrm{3}} \:{dt} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:{n}^{\mathrm{2}} \left[−\frac{\mathrm{1}}{\mathrm{2}}{t}^{−\mathrm{2}} \right]_{{n}} ^{{n}+\mathrm{1}} \:=−\frac{\mathrm{1}}{\mathrm{2}}\sum_{{n}=\mathrm{1}} ^{\infty} \:{n}^{\mathrm{2}} \left\{\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right\} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\sum_{{n}=\mathrm{1}} ^{\infty} \left(\frac{{n}^{\mathrm{2}} }{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }−\mathrm{1}\right)\:=−\frac{\mathrm{1}}{\mathrm{2}}\sum_{{n}=\mathrm{1}} ^{\infty} \left(\frac{{n}^{\mathrm{2}} −\left({n}^{\mathrm{2}} +\mathrm{2}{n}+\mathrm{1}\right)}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \frac{−\mathrm{2}{n}−\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:\:{and}\:{this}\:{serie}\:{is}\:{divergente} \\ $$$${because}\:\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:\sim\frac{\mathrm{1}}{{n}}\left(\:{n}\sim+\infty\right) \\ $$
Answered by mahdi last updated on 08/Apr/20
![(1/x)=[(1/x)]+{(1/x)}⇒x{(1/x)}[(1/x)]=x((1/x)−[(1/x)])[(1/x)] =[(1/x)]−x[(1/x)]^2 ∫_0 ^1 x{(1/x)}[(1/x)]dx=∫_0 ^1 ([(1/x)]−x[(1/x)]^2 )dx= Σ_(n=1) ^∞ ∫_(1/(n+1)) ^(1/n) ([(1/x)]−x[(1/x)]^2 )dx= Σ_(n=1) ^∞ ∫_(1/(n+1)) ^(1/n) (n−xn^2 )dx=Σ_(n=1) ^∞ [nx−((x^2 n^2 )/2)]_(1/(n+1)) ^(1/n) Σ_(n=1) ^∞ ((1/(n+1))−(1/(2(n+1)^2 )))=Σ_(n=1) ^∞ (((2n+1)/(2(n+1)^2 )))](https://www.tinkutara.com/question/Q88125.png)
$$\frac{\mathrm{1}}{\mathrm{x}}=\left[\frac{\mathrm{1}}{\mathrm{x}}\right]+\left\{\frac{\mathrm{1}}{\mathrm{x}}\right\}\Rightarrow\mathrm{x}\left\{\frac{\mathrm{1}}{\mathrm{x}}\right\}\left[\frac{\mathrm{1}}{\mathrm{x}}\right]=\mathrm{x}\left(\frac{\mathrm{1}}{\mathrm{x}}−\left[\frac{\mathrm{1}}{\mathrm{x}}\right]\right)\left[\frac{\mathrm{1}}{\mathrm{x}}\right] \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{x}}\right]−\mathrm{x}\left[\frac{\mathrm{1}}{\mathrm{x}}\right]^{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}\left\{\frac{\mathrm{1}}{\mathrm{x}}\right\}\left[\frac{\mathrm{1}}{\mathrm{x}}\right]\mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\left[\frac{\mathrm{1}}{\mathrm{x}}\right]−\mathrm{x}\left[\frac{\mathrm{1}}{\mathrm{x}}\right]^{\mathrm{2}} \right)\mathrm{dx}= \\ $$$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}} ^{\frac{\mathrm{1}}{\mathrm{n}}} \left(\left[\frac{\mathrm{1}}{\mathrm{x}}\right]−\mathrm{x}\left[\frac{\mathrm{1}}{\mathrm{x}}\right]^{\mathrm{2}} \right)\mathrm{dx}= \\ $$$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}} ^{\frac{\mathrm{1}}{\mathrm{n}}} \left(\mathrm{n}−\mathrm{xn}^{\mathrm{2}} \right)\mathrm{dx}=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\mathrm{nx}−\frac{\mathrm{x}^{\mathrm{2}} \mathrm{n}^{\mathrm{2}} }{\mathrm{2}}\right]_{\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}} ^{\frac{\mathrm{1}}{\mathrm{n}}} \\ $$$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\right)=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{2n}+\mathrm{1}}{\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$ \\ $$
Commented by mahdi last updated on 08/Apr/20
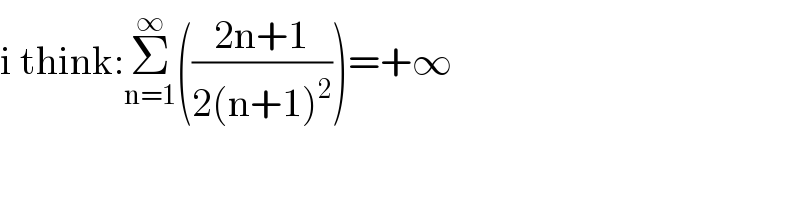
$$\mathrm{i}\:\mathrm{think}:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{2n}+\mathrm{1}}{\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\right)=+\infty \\ $$
