Question-88071

Question Number 88071 by ar247 last updated on 08/Apr/20

Commented by ar247 last updated on 08/Apr/20

$${help}\:{please} \\ $$

Commented by jagoll last updated on 08/Apr/20

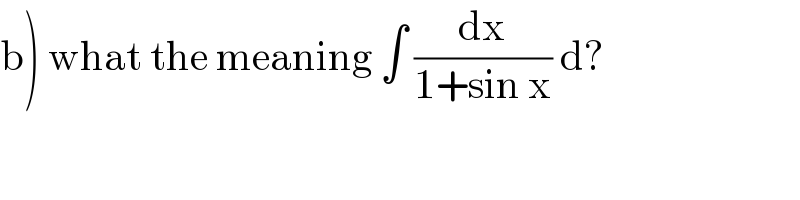
$$\left.\mathrm{b}\right)\:\mathrm{what}\:\mathrm{the}\:\mathrm{meaning}\:\int\:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}\:\mathrm{d}? \\ $$

Commented by ar247 last updated on 08/Apr/20

$$\left.{b}\right)\:\int\frac{{dx}}{\mathrm{1}+{sin}\:{x}}\:{typo} \\ $$

Commented by john santu last updated on 08/Apr/20

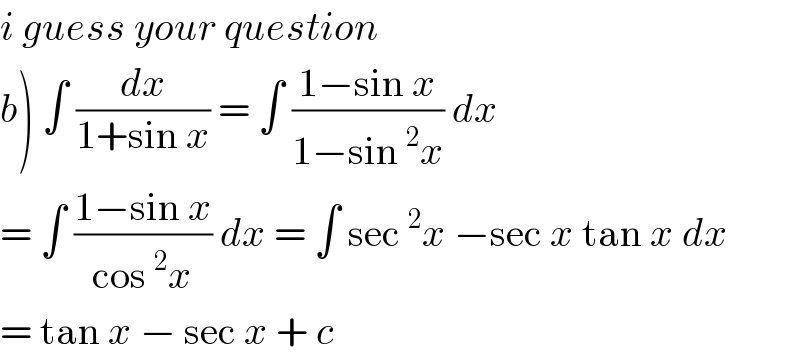
i guess your question b) ∫ (dx/(1+sin x)) = ∫ ((1−sin x)/(1−sin^2 x)) dx = ∫ ((1−sin x)/(cos^2 x)) dx = ∫ sec^2 x −sec x tan x dx = tan x − sec x + c

$${i}\:{guess}\:{your}\:{question} \\ $$$$\left.{b}\right)\:\int\:\frac{{dx}}{\mathrm{1}+\mathrm{sin}\:{x}}\:=\:\int\:\frac{\mathrm{1}−\mathrm{sin}\:{x}}{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {x}}\:{dx} \\ $$$$=\:\int\:\frac{\mathrm{1}−\mathrm{sin}\:{x}}{\mathrm{cos}\:^{\mathrm{2}} {x}}\:{dx}\:=\:\int\:\mathrm{sec}\:^{\mathrm{2}} {x}\:−\mathrm{sec}\:{x}\:\mathrm{tan}\:{x}\:{dx} \\ $$$$=\:\mathrm{tan}\:{x}\:−\:\mathrm{sec}\:{x}\:+\:{c}\: \\ $$

Commented by ar247 last updated on 08/Apr/20

$${help}\:{please} \\ $$

Commented by mathmax by abdo last updated on 08/Apr/20

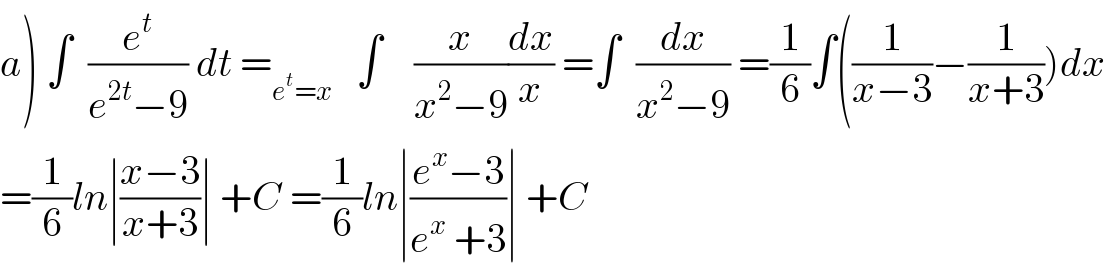
a) ∫ (e^t /(e^(2t) −9)) dt =_(e^t =x) ∫ (x/(x^2 −9))(dx/x) =∫ (dx/(x^2 −9)) =(1/6)∫((1/(x−3))−(1/(x+3)))dx =(1/6)ln∣((x−3)/(x+3))∣ +C =(1/6)ln∣((e^x −3)/(e^x +3))∣ +C

$$\left.{a}\right)\:\int\:\:\frac{{e}^{{t}} }{{e}^{\mathrm{2}{t}} −\mathrm{9}}\:{dt}\:=_{{e}^{{t}} ={x}} \:\:\:\int\:\:\:\:\frac{{x}}{{x}^{\mathrm{2}} −\mathrm{9}}\frac{{dx}}{{x}}\:=\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} −\mathrm{9}}\:=\frac{\mathrm{1}}{\mathrm{6}}\int\left(\frac{\mathrm{1}}{{x}−\mathrm{3}}−\frac{\mathrm{1}}{{x}+\mathrm{3}}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}{ln}\mid\frac{{x}−\mathrm{3}}{{x}+\mathrm{3}}\mid\:+{C}\:=\frac{\mathrm{1}}{\mathrm{6}}{ln}\mid\frac{{e}^{{x}} −\mathrm{3}}{{e}^{{x}} \:+\mathrm{3}}\mid\:+{C} \\ $$

Commented by mathmax by abdo last updated on 08/Apr/20

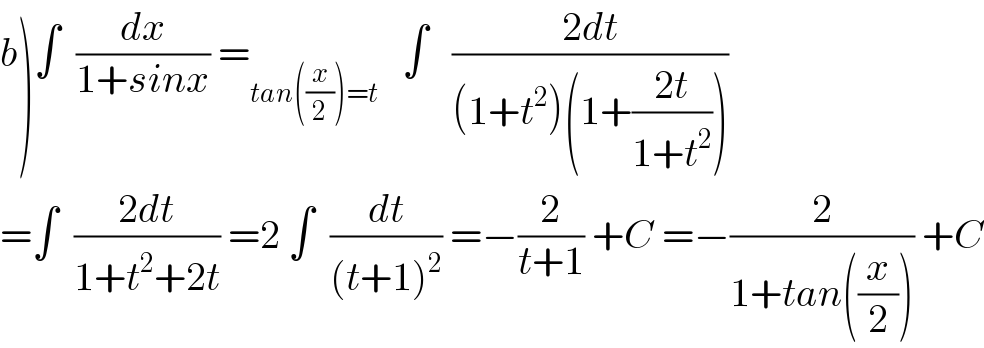
b)∫ (dx/(1+sinx)) =_(tan((x/2))=t) ∫ ((2dt)/((1+t^2 )(1+((2t)/(1+t^2 ))))) =∫ ((2dt)/(1+t^2 +2t)) =2 ∫ (dt/((t+1)^2 )) =−(2/(t+1)) +C =−(2/(1+tan((x/2)))) +C

$$\left.{b}\right)\int\:\:\frac{{dx}}{\mathrm{1}+{sinx}}\:=_{{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}} \:\:\:\int\:\:\:\frac{\mathrm{2}{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)} \\ $$$$=\int\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} +\mathrm{2}{t}}\:=\mathrm{2}\:\int\:\:\frac{{dt}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }\:=−\frac{\mathrm{2}}{{t}+\mathrm{1}}\:+{C}\:=−\frac{\mathrm{2}}{\mathrm{1}+{tan}\left(\frac{{x}}{\mathrm{2}}\right)}\:+{C} \\ $$

Answered by john santu last updated on 08/Apr/20

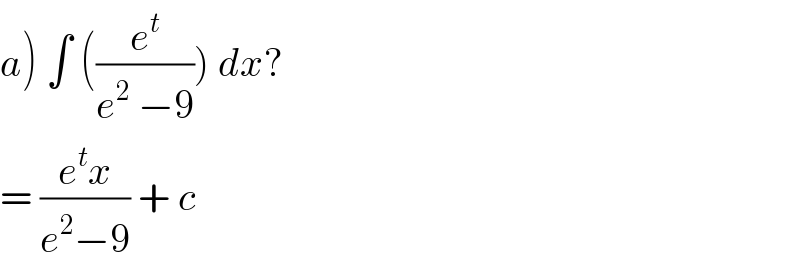
a) ∫ ((e^t /(e^2 −9))) dx? = ((e^t x)/(e^2 −9)) + c

$$\left.{a}\right)\:\int\:\left(\frac{{e}^{{t}} }{{e}^{\mathrm{2}} \:−\mathrm{9}}\right)\:{dx}?\: \\ $$$$=\:\frac{{e}^{{t}} {x}}{{e}^{\mathrm{2}} −\mathrm{9}}\:+\:{c} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply