Question Number 88153 by Chi Mes Try last updated on 08/Apr/20
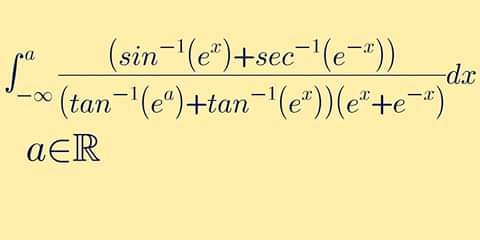
Commented by Prithwish Sen 1 last updated on 08/Apr/20

$$\mathrm{sin}^{−\mathrm{1}} \mathrm{e}^{\mathrm{x}} \:+\:\mathrm{sec}^{−\mathrm{1}} \left(\mathrm{e}^{−\mathrm{x}} \right)\:=\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{e}^{\mathrm{x}} \right)+\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{e}^{\mathrm{x}} \right)\:=\:\frac{\pi}{\mathrm{2}} \\ $$$$\frac{\pi}{\mathrm{2}}\int_{−\infty} ^{\mathrm{a}} \frac{\mathrm{e}^{\mathrm{x}} \mathrm{dx}}{\left(\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{e}^{\mathrm{a}} \right)+\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{e}^{\mathrm{x}} \right)\left(\mathrm{1}+\mathrm{e}^{\mathrm{2x}} \right)\right.} \\ $$$$\mathrm{putting}\:\mathrm{tan}\left(\mathrm{e}^{−\mathrm{x}} \right)=\:\mathrm{t} \\ $$$$=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{e}^{\mathrm{a}} \right)} \frac{\mathrm{dt}}{\mathrm{tan}^{−\mathrm{1}} \mathrm{e}^{\mathrm{a}} +\mathrm{t}}\:=\:\frac{\pi}{\mathrm{2}}\mathrm{ln}\mid\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{e}^{\mathrm{a}} \right)+\mathrm{t}\mid_{\mathrm{0}} ^{\mathrm{tan}^{−\mathrm{1}} \mathrm{e}^{\mathrm{a}} } \\ $$$$=\frac{\boldsymbol{\pi}}{\mathrm{2}}\boldsymbol{\mathrm{ln}}\mathrm{2}\:\:\:\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}}. \\ $$
