Question Number 88261 by ar247 last updated on 09/Apr/20

Answered by Joel578 last updated on 09/Apr/20
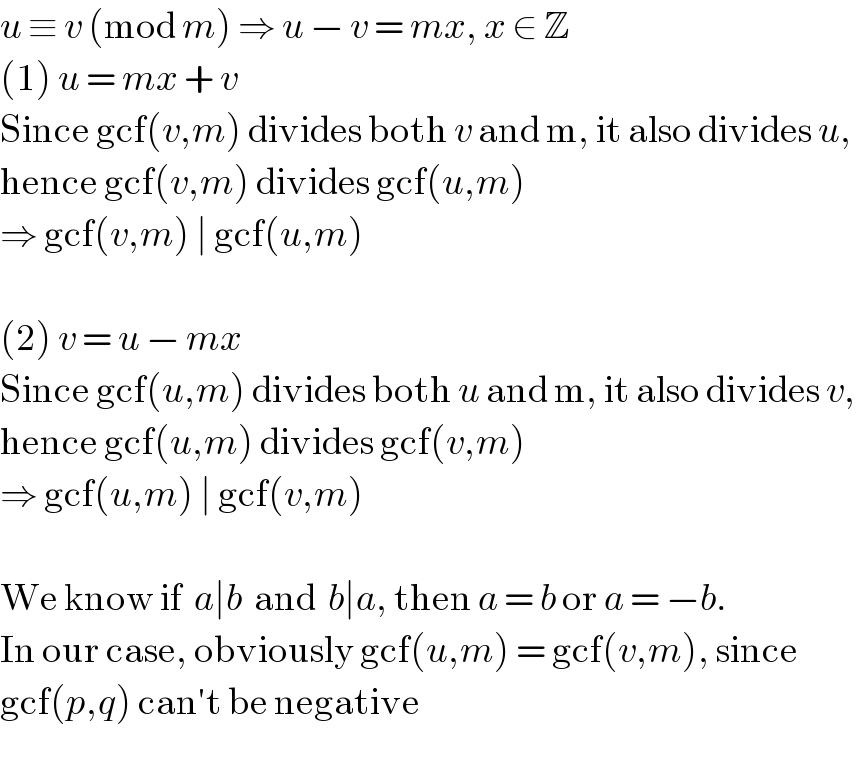
$${u}\:\equiv\:{v}\:\left(\mathrm{mod}\:{m}\right)\:\Rightarrow\:{u}\:−\:{v}\:=\:{mx},\:{x}\:\in\:\mathbb{Z} \\ $$$$\left(\mathrm{1}\right)\:{u}\:=\:{mx}\:+\:{v} \\ $$$$\mathrm{Since}\:\mathrm{gcf}\left({v},{m}\right)\:\mathrm{divides}\:\mathrm{both}\:{v}\:\mathrm{and}\:\mathrm{m},\:\mathrm{it}\:\mathrm{also}\:\mathrm{divides}\:{u}, \\ $$$$\mathrm{hence}\:\mathrm{gcf}\left({v},{m}\right)\:\mathrm{divides}\:\mathrm{gcf}\left({u},{m}\right) \\ $$$$\Rightarrow\:\mathrm{gcf}\left({v},{m}\right)\:\mid\:\mathrm{gcf}\left({u},{m}\right) \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\:{v}\:=\:{u}\:−\:{mx} \\ $$$$\mathrm{Since}\:\mathrm{gcf}\left({u},{m}\right)\:\mathrm{divides}\:\mathrm{both}\:{u}\:\mathrm{and}\:\mathrm{m},\:\mathrm{it}\:\mathrm{also}\:\mathrm{divides}\:{v}, \\ $$$$\mathrm{hence}\:\mathrm{gcf}\left({u},{m}\right)\:\mathrm{divides}\:\mathrm{gcf}\left({v},{m}\right) \\ $$$$\Rightarrow\:\mathrm{gcf}\left({u},{m}\right)\:\mid\:\mathrm{gcf}\left({v},{m}\right) \\ $$$$ \\ $$$$\mathrm{We}\:\mathrm{know}\:\mathrm{if}\:\:{a}\mid{b}\:\:\mathrm{and}\:\:{b}\mid{a},\:\mathrm{then}\:{a}\:=\:{b}\:\mathrm{or}\:{a}\:=\:−{b}. \\ $$$$\mathrm{In}\:\mathrm{our}\:\mathrm{case},\:\mathrm{obviously}\:\mathrm{gcf}\left({u},{m}\right)\:=\:\mathrm{gcf}\left({v},{m}\right),\:\mathrm{since} \\ $$$$\mathrm{gcf}\left({p},{q}\right)\:\mathrm{can}'\mathrm{t}\:\mathrm{be}\:\mathrm{negative} \\ $$
