Menu Close

Question-88272

Tinku Tara 0 Comments
Pin




Question Number 88272 by ajfour last updated on 09/Apr/20
Commented by ajfour last updated on 09/Apr/20
Find radius of semicircle in terms of ellipse parameters a and b. (a>b)
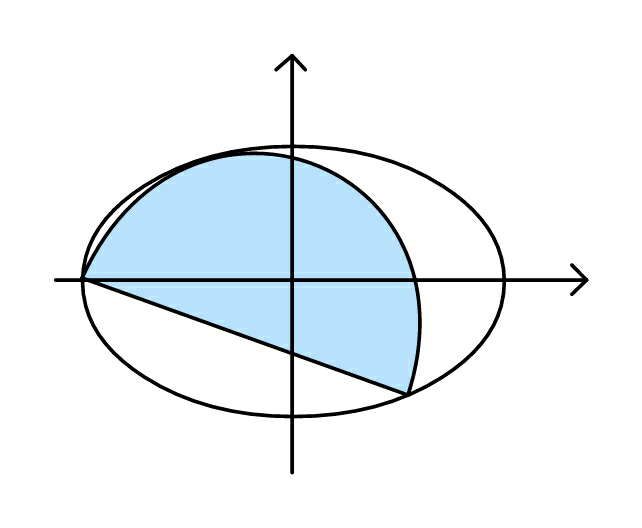
$${Find}\:{radius}\:{of}\:{semicircle}\:{in} \\ $$$${terms}\:{of}\:{ellipse}\:{parameters} \\ $$$${a}\:{and}\:{b}.\:\:\left({a}>{b}\right) \\ $$
Answered by mr W last updated on 09/Apr/20
Commented by mr W last updated on 10/Apr/20
let μ=(b/a) say P(a cos θ, b sin θ) (dy/dx)=((b cos θ)/(−a sin θ))=−(μ/(tan θ)) tan ϕ=−(1/(dy/dx))=((tan θ)/μ)=((sin θ)/(μ cos θ)) ⇒sin ϕ=((sin θ)/( (√(sin^2 θ+μ^2 cos^2 θ)) )) ⇒cos ϕ=((μ cos θ)/( (√(sin^2 θ+μ^2 cos^2 θ)) )) x_s =a cos θ −r cos ϕ y_s =b sin θ −r sin ϕ (a−x_s )^2 +y_s ^2 =r^2 (a−a cos θ +r cos ϕ)^2 +(b sin θ −r sin ϕ)^2 =r^2 a^2 (1−cos θ)^2 +2ar(1−cos θ) cos ϕ+b^2 sin^2 θ −2br sin θ sin ϕ=0 a^2 (1−cos θ)^2 +2ar(((1−cos θ)μ cos θ)/( (√(sin^2 θ+μ^2 cos^2 θ))))+b^2 sin^2 θ −2br((sin θ sin θ)/( (√(sin^2 θ+μ^2 cos^2 θ))))=0 with λ=(r/a) ⇒(1−cos θ)^2 +μ^2 sin^2 θ =2μλ((1−cos θ)/( (√(sin^2 θ+μ^2 cos^2 θ)) )) ⇒λ=(([1+μ^2 −(1−μ^2 )cos θ](√(sin^2 θ+μ^2 cos^2 θ)))/(2μ)) ...(i) x_R =2x_s −a x_R =−a(1−2cos θ)−2r cos ϕ=−a(1−2cos θ)−((2μr cos θ)/( (√(sin^2 θ+μ^2 cos^2 θ)) )) y_R =2y_s y_R =2(b sin θ −r sin ϕ)=2sin θ(b−(r/( (√(sin^2 θ+μ^2 cos^2 θ)) ))) (x_R ^2 /a^2 )+(y_R ^2 /b^2 )=1 b^2 [a(1−2 cos θ)+((2μr cos θ)/( (√(sin^2 θ+μ^2 cos^2 θ))))]^2 +4a^2 sin^2 θ(b−(r/( (√(sin^2 θ+μ^2 cos^2 θ)) )))^2 =a^2 b^2 ⇒[1−2 cos θ+((2μλ cos θ)/( (√(sin^2 θ+μ^2 cos^2 θ))))]^2 +4 sin^2 θ(1−(λ/(μ(√(sin^2 θ+μ^2 cos^2 θ)) )))^2 =1 ⇒(1−μ^2 )[μ^4 cos^2 θ(1+cos θ)+(1−cos θ)^3 ]=2μ^4 cos θ ...(ii) from (i) and (ii) we can get θ and λ. example: a=4, b=3⇒μ=(3/4) ⇒θ=73.7398° ⇒λ=0.9434
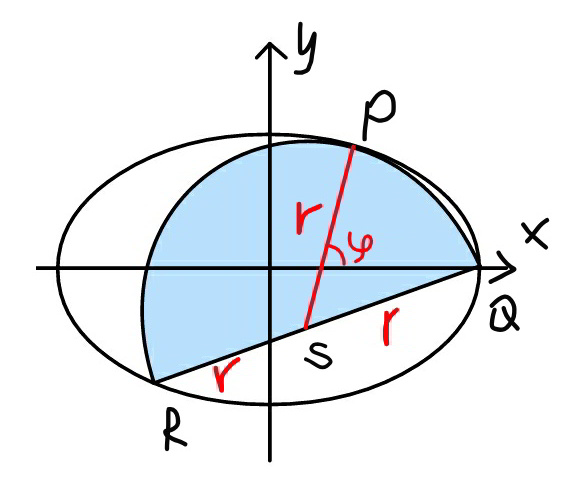
$${let}\:\mu=\frac{{b}}{{a}} \\ $$$${say}\:{P}\left({a}\:\mathrm{cos}\:\theta,\:{b}\:\mathrm{sin}\:\theta\right) \\ $$$$\frac{{dy}}{{dx}}=\frac{{b}\:\mathrm{cos}\:\theta}{−{a}\:\mathrm{sin}\:\theta}=−\frac{\mu}{\mathrm{tan}\:\theta} \\ $$$$\mathrm{tan}\:\varphi=−\frac{\mathrm{1}}{\frac{{dy}}{{dx}}}=\frac{\mathrm{tan}\:\theta}{\mu}=\frac{\mathrm{sin}\:\theta}{\mu\:\mathrm{cos}\:\theta} \\ $$$$\Rightarrow\mathrm{sin}\:\varphi=\frac{\mathrm{sin}\:\theta}{\:\sqrt{\mathrm{sin}^{\mathrm{2}} \:\theta+\mu^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}\:} \\ $$$$\Rightarrow\mathrm{cos}\:\varphi=\frac{\mu\:\mathrm{cos}\:\theta}{\:\sqrt{\mathrm{sin}^{\mathrm{2}} \:\theta+\mu^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}\:} \\ $$$$ \\ $$$${x}_{{s}} ={a}\:\mathrm{cos}\:\theta\:−{r}\:\mathrm{cos}\:\varphi \\ $$$${y}_{{s}} ={b}\:\mathrm{sin}\:\theta\:−{r}\:\mathrm{sin}\:\varphi \\ $$$$\left({a}−{x}_{{s}} \right)^{\mathrm{2}} +{y}_{{s}} ^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\left({a}−{a}\:\mathrm{cos}\:\theta\:+{r}\:\mathrm{cos}\:\varphi\right)^{\mathrm{2}} +\left({b}\:\mathrm{sin}\:\theta\:−{r}\:\mathrm{sin}\:\varphi\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} \:+\mathrm{2}{ar}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)\:\mathrm{cos}\:\varphi+{b}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta\:−\mathrm{2}{br}\:\mathrm{sin}\:\theta\:\mathrm{sin}\:\varphi=\mathrm{0} \\ $$$${a}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} \:+\mathrm{2}{ar}\frac{\left(\mathrm{1}−\mathrm{cos}\:\theta\right)\mu\:\mathrm{cos}\:\theta}{\:\sqrt{\mathrm{sin}^{\mathrm{2}} \:\theta+\mu^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}}+{b}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta\:−\mathrm{2}{br}\frac{\mathrm{sin}\:\theta\:\mathrm{sin}\:\theta}{\:\sqrt{\mathrm{sin}^{\mathrm{2}} \:\theta+\mu^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}}=\mathrm{0} \\ $$$${with}\:\lambda=\frac{{r}}{{a}} \\ $$$$\Rightarrow\left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} +\mu^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta\:=\mathrm{2}\mu\lambda\frac{\mathrm{1}−\mathrm{cos}\:\theta}{\:\sqrt{\mathrm{sin}^{\mathrm{2}} \:\theta+\mu^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta}\:} \\ $$$$\Rightarrow\lambda=\frac{\left[\mathrm{1}+\mu^{\mathrm{2}} −\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\mathrm{cos}\:\theta\right]\sqrt{\mathrm{sin}^{\mathrm{2}} \:\theta+\mu^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta}}{\mathrm{2}\mu}\:\:\:…\left({i}\right) \\ $$$$ \\ $$$${x}_{{R}} =\mathrm{2}{x}_{{s}} −{a} \\ $$$${x}_{{R}} =−{a}\left(\mathrm{1}−\mathrm{2cos}\:\theta\right)−\mathrm{2}{r}\:\mathrm{cos}\:\varphi=−{a}\left(\mathrm{1}−\mathrm{2cos}\:\theta\right)−\frac{\mathrm{2}\mu{r}\:\mathrm{cos}\:\theta}{\:\sqrt{\mathrm{sin}^{\mathrm{2}} \:\theta+\mu^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}\:} \\ $$$${y}_{{R}} =\mathrm{2}{y}_{{s}} \\ $$$${y}_{{R}} =\mathrm{2}\left({b}\:\mathrm{sin}\:\theta\:−{r}\:\mathrm{sin}\:\varphi\right)=\mathrm{2sin}\:\theta\left({b}−\frac{{r}}{\:\sqrt{\mathrm{sin}^{\mathrm{2}} \:\theta+\mu^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}\:}\right) \\ $$$$\frac{{x}_{{R}} ^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}_{{R}} ^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${b}^{\mathrm{2}} \left[{a}\left(\mathrm{1}−\mathrm{2}\:\mathrm{cos}\:\theta\right)+\frac{\mathrm{2}\mu{r}\:\mathrm{cos}\:\theta}{\:\sqrt{\mathrm{sin}^{\mathrm{2}} \:\theta+\mu^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}}\right]^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta\left({b}−\frac{{r}}{\:\sqrt{\mathrm{sin}^{\mathrm{2}} \:\theta+\mu^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}\:}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\Rightarrow\left[\mathrm{1}−\mathrm{2}\:\mathrm{cos}\:\theta+\frac{\mathrm{2}\mu\lambda\:\mathrm{cos}\:\theta}{\:\sqrt{\mathrm{sin}^{\mathrm{2}} \:\theta+\mu^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}}\right]^{\mathrm{2}} +\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\theta\left(\mathrm{1}−\frac{\lambda}{\mu\sqrt{\mathrm{sin}^{\mathrm{2}} \:\theta+\mu^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta}\:}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\left[\mu^{\mathrm{4}} \mathrm{cos}^{\mathrm{2}} \:\theta\left(\mathrm{1}+\mathrm{cos}\:\theta\right)+\left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{3}} \right]=\mathrm{2}\mu^{\mathrm{4}} \:\mathrm{cos}\:\theta\:\:…\left({ii}\right) \\ $$$$ \\ $$$${from}\:\left({i}\right)\:{and}\:\left({ii}\right)\:{we}\:{can}\:{get}\:\theta\:{and}\:\lambda. \\ $$$$ \\ $$$${example}:\:{a}=\mathrm{4},\:{b}=\mathrm{3}\Rightarrow\mu=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\theta=\mathrm{73}.\mathrm{7398}° \\ $$$$\Rightarrow\lambda=\mathrm{0}.\mathrm{9434} \\ $$
Commented by ajfour last updated on 10/Apr/20
Thanks sir!
$${Thanks}\:{sir}! \\ $$
Commented by liki last updated on 09/Apr/20
...sory mr W , how to get your contact i need help for you ; my contact +255745266946
$$…\boldsymbol{{sory}}\:\boldsymbol{{mr}}\:\boldsymbol{{W}}\:,\:{how}\:{to}\:{get}\:{your}\:{contact}\:{i}\:{need}\:{help}\:{for}\:{you}\:;\:{my}\:{contact}\:+\mathrm{255745266946}\: \\ $$
Commented by mr W last updated on 09/Apr/20
sorry sir, if i could help you, i can do it only within this forum. so, when you have a question, just post it here.
$${sorry}\:{sir},\:{if}\:{i}\:{could}\:{help}\:{you},\:{i}\:{can}\:{do}\:{it} \\ $$$${only}\:{within}\:{this}\:{forum}.\:{so},\:{when}\:{you} \\ $$$${have}\:{a}\:{question},\:{just}\:{post}\:{it}\:{here}. \\ $$
Commented by liki last updated on 09/Apr/20
..there is something i want to ask you sir, thus why i wrote my whatssap no
$$..{there}\:{is}\:{something}\:{i}\:{want}\:{to}\:{ask}\:{you}\:{sir},\:{thus}\:{why}\:{i}\:{wrote}\:{my}\:{whatssap}\:{no} \\ $$
Commented by Ar Brandon last updated on 09/Apr/20
Oh my !
$${Oh}\:{my}\:! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *