Question Number 88288 by Chi Mes Try last updated on 09/Apr/20
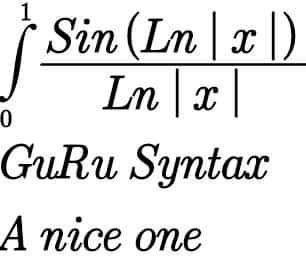
Commented by abdomathmax last updated on 10/Apr/20
![I =∫_0 ^1 ((sin(ln∣x∣))/(ln∣x∣))dx changement ln(x)=−u ⇒ I =∫_0 ^1 ((sin(lnx))/(lnx))dx =−∫_0 ^(+∞) ((−sinu)/(−u))(−e^(−u) )du = ∫_0 ^∞ ((sinu)/u) e^(−u) du let f(t) =∫_0 ^∞ ((sinu)/u)e^(−tu) du with t>0 f^′ (t) =−∫_0 ^∞ e^(−tu) sinu du =−Im(∫_0 ^∞ e^(−tu+iu) du) =−Im(∫_0 ^∞ e^((−t+i)u) du) ∫_0 ^∞ e^((−t+i)u) du =[(1/(−t+i))e^((−t+i)u) ]_0 ^(+∞) =((−1)/(−t+i)) =(1/(t−i)) =((t+i)/(t^2 +1)) ⇒f^′ (t)=−(1/(1+t^2 )) ⇒ f(t) =k−arctant lim_(t→0) f(t) =∫_0 ^∞ ((sinu)/u)du =(π/2)=k ⇒ f(t) =(π/2) −arcrant (t>0) I =f(1) =(π/2)−(π/4) =(π/4)](https://www.tinkutara.com/question/Q88334.png)
$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{sin}\left({ln}\mid{x}\mid\right)}{{ln}\mid{x}\mid}{dx}\:\:{changement}\:\:{ln}\left({x}\right)=−{u}\:\Rightarrow \\ $$$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{sin}\left({lnx}\right)}{{lnx}}{dx}\:=−\int_{\mathrm{0}} ^{+\infty} \:\frac{−{sinu}}{−{u}}\left(−{e}^{−{u}} \right){du} \\ $$$$=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sinu}}{{u}}\:{e}^{−{u}} \:{du}\:\:{let}\:{f}\left({t}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sinu}}{{u}}{e}^{−{tu}} \:{du} \\ $$$${with}\:{t}>\mathrm{0} \\ $$$${f}^{'} \left({t}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:{e}^{−{tu}} \:{sinu}\:{du}\: \\ $$$$=−{Im}\left(\int_{\mathrm{0}} ^{\infty} \:{e}^{−{tu}+{iu}} {du}\right)\:=−{Im}\left(\int_{\mathrm{0}} ^{\infty} \:{e}^{\left(−{t}+{i}\right){u}} \:{du}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{\left(−{t}+{i}\right){u}} {du}\:=\left[\frac{\mathrm{1}}{−{t}+{i}}{e}^{\left(−{t}+{i}\right){u}} \right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\frac{−\mathrm{1}}{−{t}+{i}}\:=\frac{\mathrm{1}}{{t}−{i}}\:=\frac{{t}+{i}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow{f}^{'} \left({t}\right)=−\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\Rightarrow \\ $$$${f}\left({t}\right)\:={k}−{arctant} \\ $$$${lim}_{{t}\rightarrow\mathrm{0}} {f}\left({t}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{sinu}}{{u}}{du}\:=\frac{\pi}{\mathrm{2}}={k}\:\Rightarrow \\ $$$${f}\left({t}\right)\:=\frac{\pi}{\mathrm{2}}\:−{arcrant}\:\:\:\left({t}>\mathrm{0}\right) \\ $$$${I}\:={f}\left(\mathrm{1}\right)\:=\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\:=\frac{\pi}{\mathrm{4}} \\ $$
Answered by mind is power last updated on 09/Apr/20
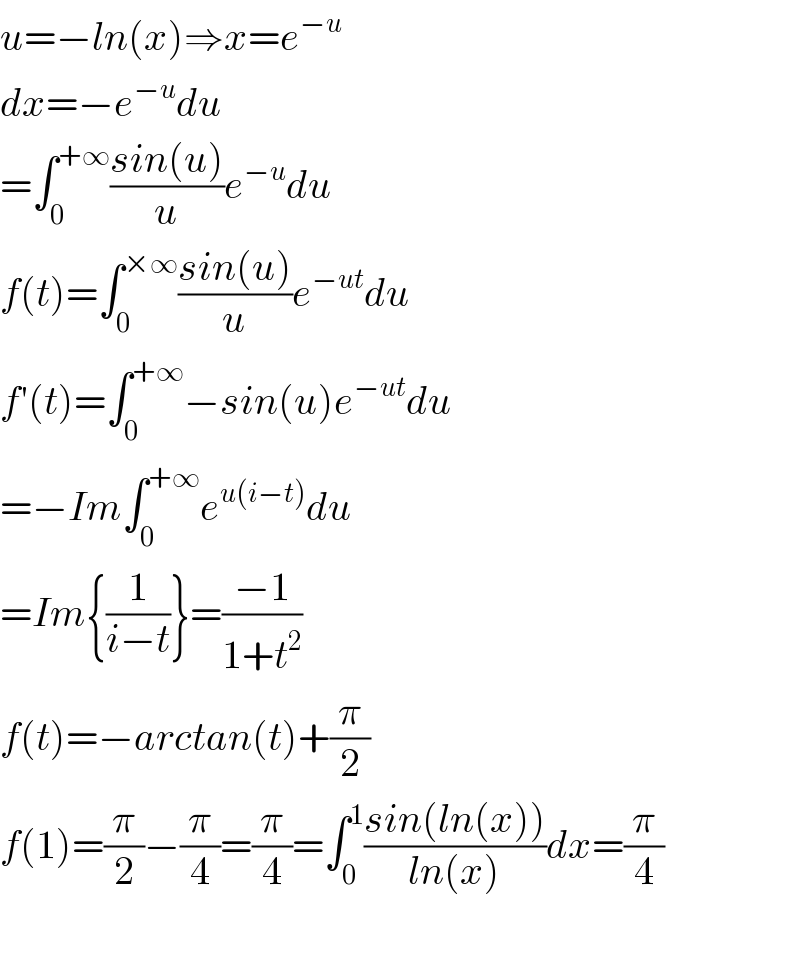
$${u}=−{ln}\left({x}\right)\Rightarrow{x}={e}^{−{u}} \\ $$$${dx}=−{e}^{−{u}} {du} \\ $$$$=\int_{\mathrm{0}} ^{+\infty} \frac{{sin}\left({u}\right)}{{u}}{e}^{−{u}} {du} \\ $$$${f}\left({t}\right)=\int_{\mathrm{0}} ^{×\infty} \frac{{sin}\left({u}\right)}{{u}}{e}^{−{ut}} {du} \\ $$$${f}'\left({t}\right)=\int_{\mathrm{0}} ^{+\infty} −{sin}\left({u}\right){e}^{−{ut}} {du} \\ $$$$=−{Im}\int_{\mathrm{0}} ^{+\infty} {e}^{{u}\left({i}−{t}\right)} {du} \\ $$$$={Im}\left\{\frac{\mathrm{1}}{{i}−{t}}\right\}=\frac{−\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${f}\left({t}\right)=−{arctan}\left({t}\right)+\frac{\pi}{\mathrm{2}} \\ $$$${f}\left(\mathrm{1}\right)=\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}=\frac{\pi}{\mathrm{4}}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{sin}\left({ln}\left({x}\right)\right)}{{ln}\left({x}\right)}{dx}=\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$
