Question-88306

Question Number 88306 by TawaTawa1 last updated on 09/Apr/20

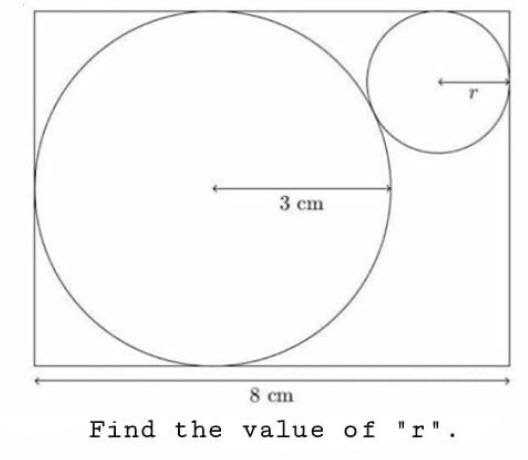
Commented by mr W last updated on 10/Apr/20

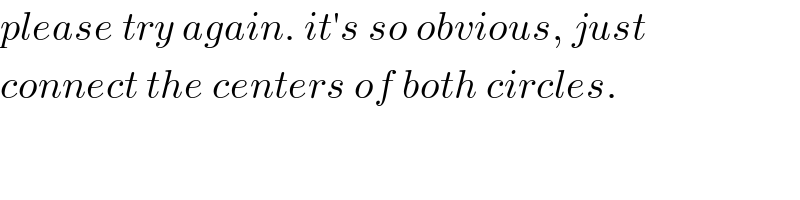
p l e a s e t r y a g a i n . {i t}^{'} s s o o b v i o u s, j u s t

c o n n e c t t h e c e n t e r s o f b o t h c i r c l e s .

Commented by mr W last updated on 09/Apr/20

{(8 - 3 - r)}^{2} + {(6 - 3 - r)}^{2} = {(3 + r)}^{2}

r^{2} - 22 r + 25 = 0

\Rightarrow r = 11 - 4 \sqrt{6} \approx 1.202

Commented by TawaTawa1 last updated on 09/Apr/20

God bless you sir .

Commented by TawaTawa1 last updated on 09/Apr/20

My problem is how you get the equation sir .

I can expand and simplify .

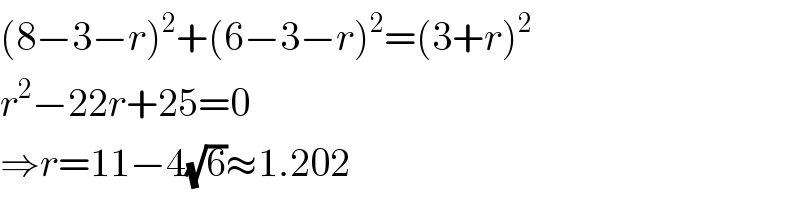
Commented by TawaTawa1 last updated on 10/Apr/20

Alright sir, i will do that