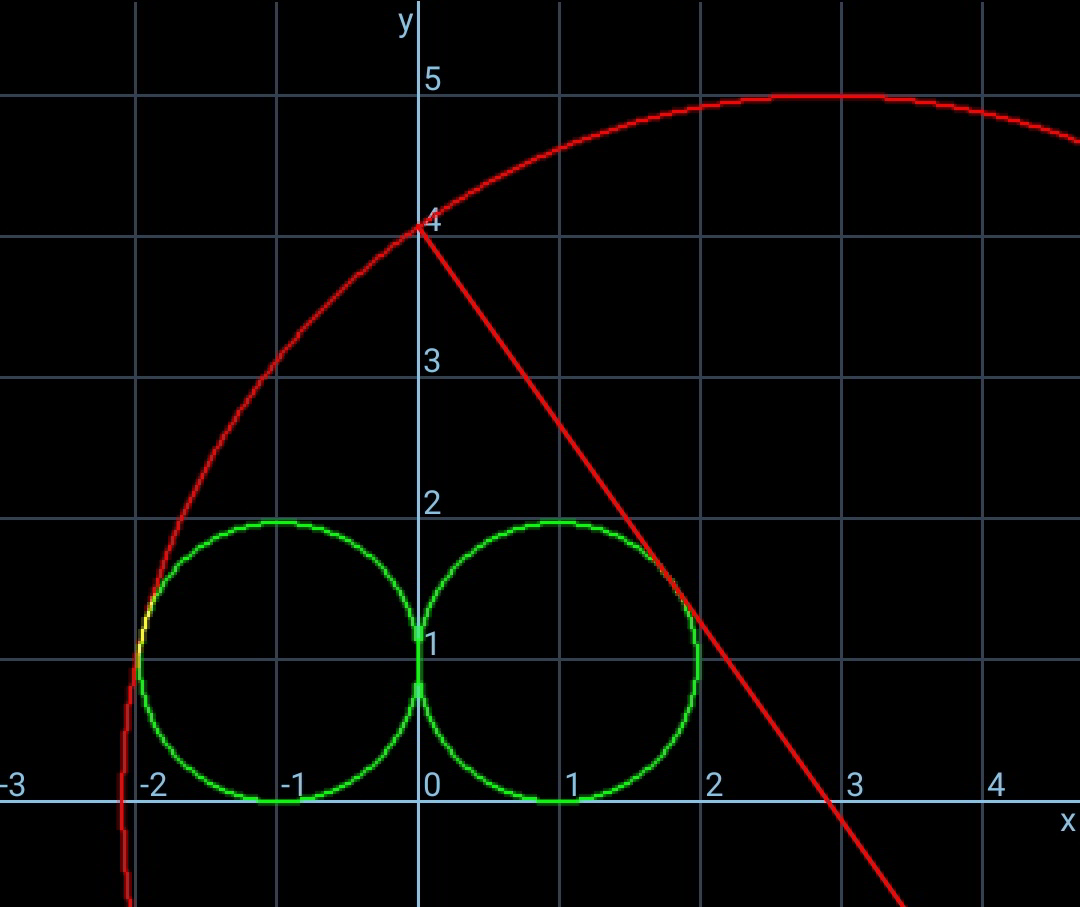
Question Number 88349 by ajfour last updated on 10/Apr/20
Commented by ajfour last updated on 10/Apr/20
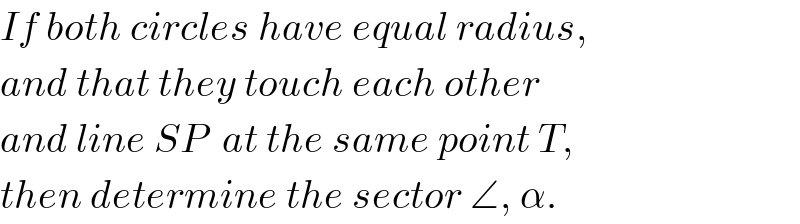
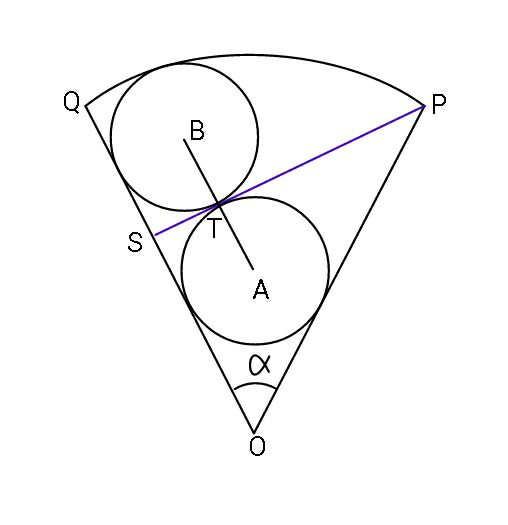
$${If}\:{both}\:{circles}\:{have}\:{equal}\:{radius}, \\ $$$${and}\:{that}\:{they}\:{touch}\:{each}\:{other} \\ $$$${and}\:{line}\:{SP}\:\:{at}\:{the}\:{same}\:{point}\:{T}, \\ $$$${then}\:{determine}\:{the}\:{sector}\:\angle,\:\alpha. \\ $$
Answered by mr W last updated on 10/Apr/20

Commented by mr W last updated on 10/Apr/20
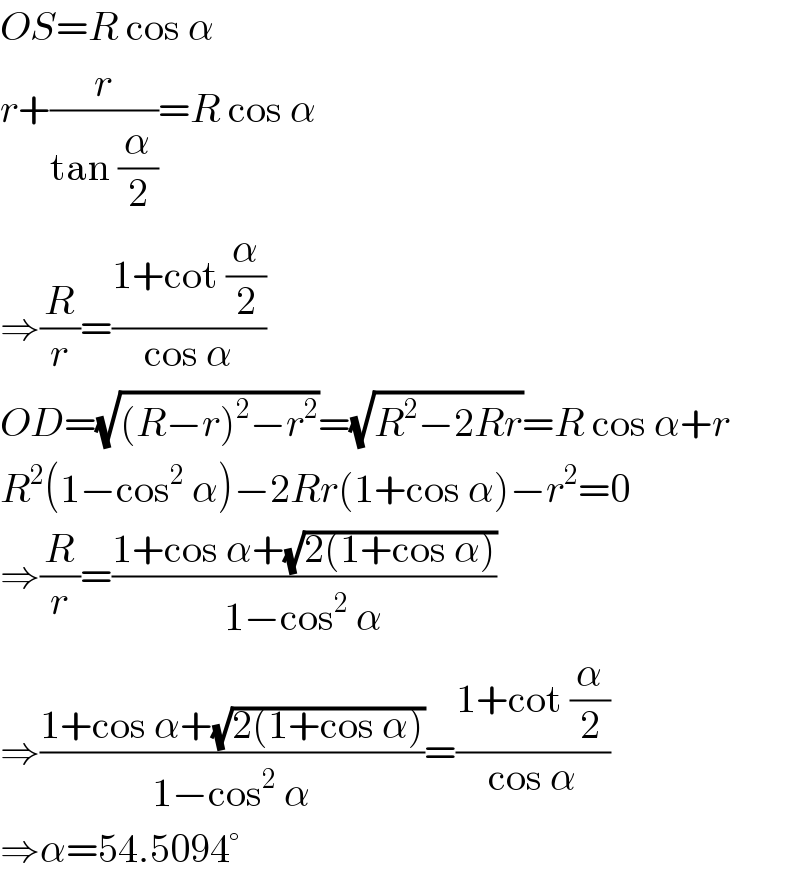
$${OS}={R}\:\mathrm{cos}\:\alpha \\ $$$${r}+\frac{{r}}{\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}}={R}\:\mathrm{cos}\:\alpha \\ $$$$\Rightarrow\frac{{R}}{{r}}=\frac{\mathrm{1}+\mathrm{cot}\:\frac{\alpha}{\mathrm{2}}}{\mathrm{cos}\:\alpha} \\ $$$${OD}=\sqrt{\left({R}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }=\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{Rr}}={R}\:\mathrm{cos}\:\alpha+{r} \\ $$$${R}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\alpha\right)−\mathrm{2}{Rr}\left(\mathrm{1}+\mathrm{cos}\:\alpha\right)−{r}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\frac{{R}}{{r}}=\frac{\mathrm{1}+\mathrm{cos}\:\alpha+\sqrt{\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:\alpha\right)}}{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\alpha} \\ $$$$\Rightarrow\frac{\mathrm{1}+\mathrm{cos}\:\alpha+\sqrt{\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:\alpha\right)}}{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\alpha}=\frac{\mathrm{1}+\mathrm{cot}\:\frac{\alpha}{\mathrm{2}}}{\mathrm{cos}\:\alpha} \\ $$$$\Rightarrow\alpha=\mathrm{54}.\mathrm{5094}° \\ $$
Commented by ajfour last updated on 10/Apr/20

$${Thanks}\:{Sir},\:{pretty}\:{good}\:{solution}, \\ $$$${If}\:{we}\:{let}\:\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}=\boldsymbol{{t}},\:{then} \\ $$$$\:\:{t}^{\mathrm{3}} −\mathrm{2}{t}^{\mathrm{2}} −\mathrm{7}{t}+\mathrm{4}=\mathrm{0} \\ $$$$\boldsymbol{\alpha}=\mathrm{2tan}^{−\mathrm{1}} \boldsymbol{{t}} \\ $$$$\:\:\:=\:\mathrm{54}.\mathrm{5094374}°\:\:\:\:\&\:\:\:\frac{{R}}{{r}}\approx\:\mathrm{5}.\mathrm{066}\:. \\ $$$${so}\:{that}\:{an}\:{accurate}\:{answer}\:{is} \\ $$$${afterall}\:{possible}.\left({just}\:{i}\:{was}\right. \\ $$$$\left.{checking}\:{again},\:{Sir}\right) \\ $$$$ \\ $$
Commented by mr W last updated on 10/Apr/20