Question Number 88352 by ajfour last updated on 10/Apr/20
Commented by ajfour last updated on 10/Apr/20
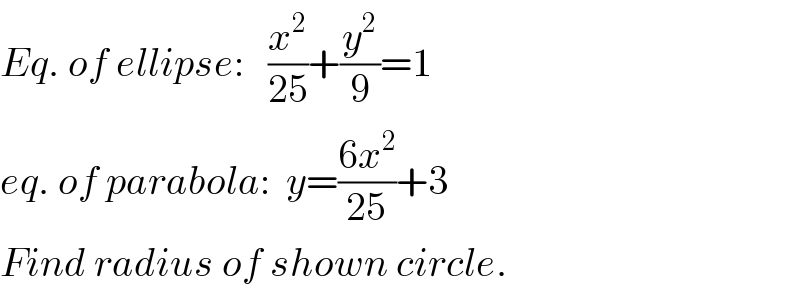
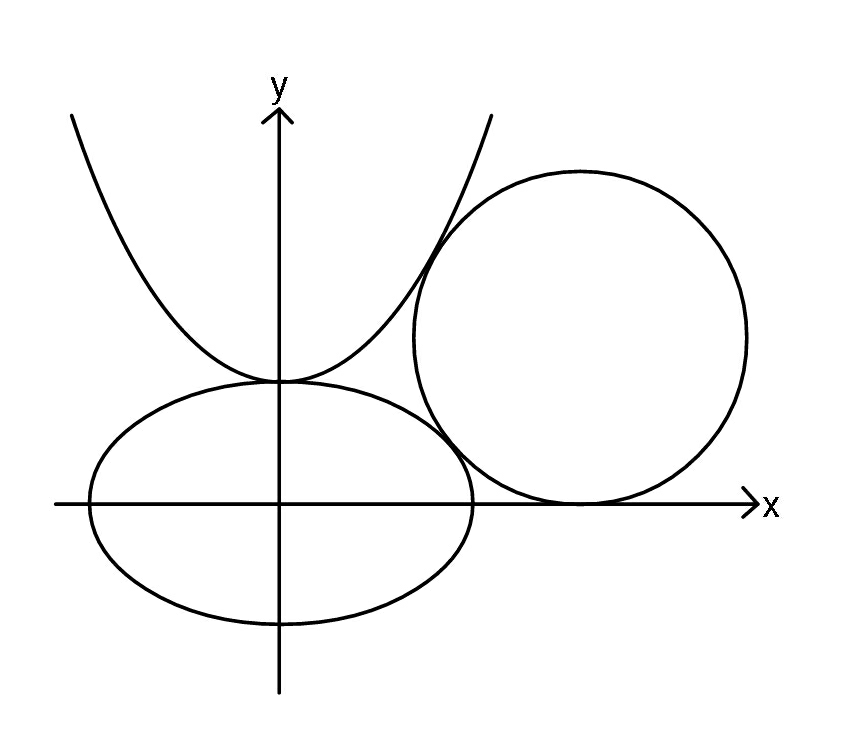
$${Eq}.\:{of}\:{ellipse}:\:\:\:\frac{{x}^{\mathrm{2}} }{\mathrm{25}}+\frac{{y}^{\mathrm{2}} }{\mathrm{9}}=\mathrm{1} \\ $$$${eq}.\:{of}\:{parabola}:\:\:{y}=\frac{\mathrm{6}{x}^{\mathrm{2}} }{\mathrm{25}}+\mathrm{3} \\ $$$${Find}\:{radius}\:{of}\:{shown}\:{circle}. \\ $$
Answered by mr W last updated on 10/Apr/20
Commented by mr W last updated on 10/Apr/20
![ellipse: (x^2 /a^2 )+(y^2 /b^2 )=1 with a=5, b=3 parabola: y=(x^2 /c)+b with c=((25)/9) say point P(p,(p^2 /c)+b) say point Q(a cos φ, b sin φ) tan θ=((2p)/c) ⇒sin θ=((2p)/( (√(4p^2 +c^2 )))) ⇒cos θ=(c/( (√(4p^2 +c^2 )))) tan ϕ=((b cos φ)/(a sin φ)) ⇒sin ϕ=((b cos φ)/( (√(a^2 sin^2 φ+b^2 cos^2 φ)))) ⇒cos ϕ=((a sin φ)/( (√(a^2 sin^2 φ+b^2 cos^2 φ)))) x_S =p+r sin θ=p+((2pr)/( (√(4p^2 +c^2 )))) y_S =(p^2 /c)+b+r cos θ=(p^2 /c)+b+((cr)/( (√(4p^2 +c^2 ))))=r ⇒(p^2 /c)+b+((cr)/( (√(4p^2 +c^2 ))))=r ⇒4p^2 +c^2 +((4cr)/( (√(4p^2 +c^2 ))))=4cr+c^2 −4bc let u=(√(4p^2 +c^2 )) ⇒u^3 −(4cr+c^2 −4bc)u+4cr=0 ⇒u=...... ⇒p=((√(u^2 −c^2 ))/2)=......in terms of r ...(i) x_S =a cos φ+r sin ϕ=cos φ(a+((br)/( (√(a^2 sin^2 φ+b^2 cos^2 φ))))) y_S =b sin φ+r cos ϕ=sin φ(b+((ar)/( (√(a^2 sin^2 φ+b^2 cos^2 φ)))))=r ⇒((br)/( (√((a^2 −b^2 )sin^2 φ+b^2 ))))=((b(r−b sin φ))/(a sin φ)) cos φ(a+((br)/( (√(a^2 sin^2 φ+b^2 cos^2 φ)))))=p+((2pr)/( (√(4p^2 +c^2 )))) (((a^2 −b^2 ) sin^2 φ+br)/(a tan φ))=p+((2pr)/( (√(4p^2 +c^2 )))) (a^2 −b^2 )((tan^2 φ)/(1+tan^2 φ))+br=(p+((2pr)/( (√(4p^2 +c^2 )))))tan φ let v=tan φ ⇒(p+((2pr)/( (√(4p^2 +c^2 )))))v^3 −(a^2 −b^2 +br)v^2 +(p+((2pr)/( (√(4p^2 +c^2 )))))v−br=0 ⇒v=...... ⇒φ=tan^(−1) v=...... in terms of p, r ...(ii) sin φ(b+((ar)/( (√(a^2 sin^2 φ+b^2 cos^2 φ)))))=r ⇒((ar)/( (√((a^2 −b^2 )sin^2 φ+b^2 ))))=((r−b sin φ)/(sin φ)) ⇒((a^2 r^2 )/((a^2 −b^2 )sin^2 φ+b^2 ))=((r^2 −2br sin φ+b^2 sin^2 φ)/(sin^2 φ)) [r^2 −2br sin φ+b^2 sin^2 φ][(a^2 −b^2 )sin^2 φ+b^2 ]=a^2 r^2 sin^2 φ ⇒(a^2 −b^2 )b sin^4 φ−2(a^2 −b^2 )r sin^3 φ−b(r^2 −b^2 )sin^2 φ−2b^2 r sin φ+br^2 =0 ...(iii) with (i) and (ii) in (iii) we can get r. .....](https://www.tinkutara.com/question/Q88359.png)
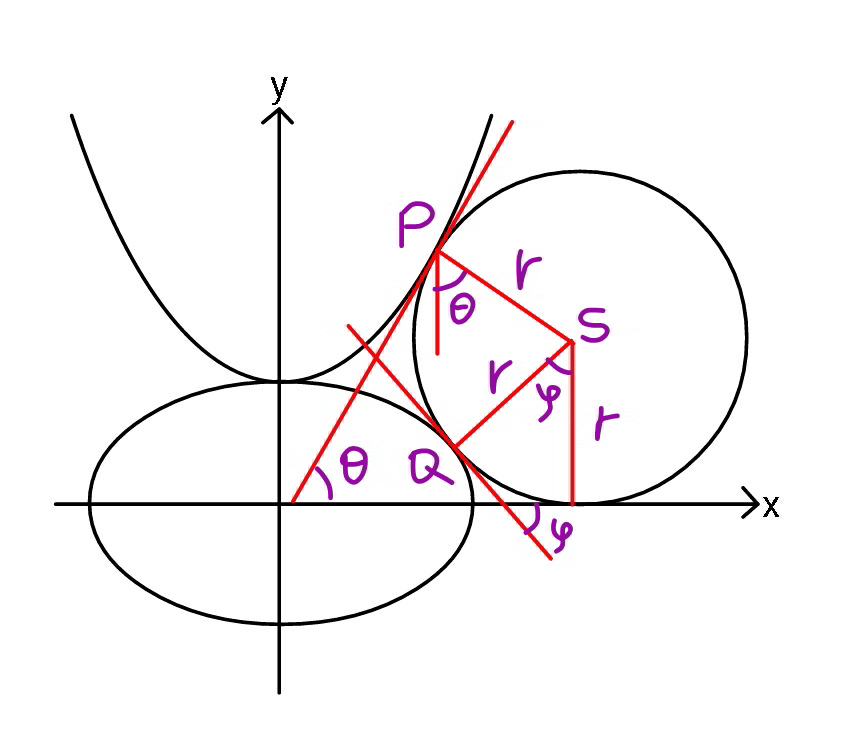
$${ellipse}: \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:{with}\:{a}=\mathrm{5},\:{b}=\mathrm{3} \\ $$$${parabola}: \\ $$$${y}=\frac{{x}^{\mathrm{2}} }{{c}}+{b}\:{with}\:{c}=\frac{\mathrm{25}}{\mathrm{9}} \\ $$$$ \\ $$$${say}\:{point}\:{P}\left({p},\frac{{p}^{\mathrm{2}} }{{c}}+{b}\right) \\ $$$${say}\:{point}\:{Q}\left({a}\:\mathrm{cos}\:\phi,\:{b}\:\mathrm{sin}\:\phi\right) \\ $$$$\mathrm{tan}\:\theta=\frac{\mathrm{2}{p}}{{c}} \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\frac{\mathrm{2}{p}}{\:\sqrt{\mathrm{4}{p}^{\mathrm{2}} +{c}^{\mathrm{2}} }} \\ $$$$\Rightarrow\mathrm{cos}\:\theta=\frac{{c}}{\:\sqrt{\mathrm{4}{p}^{\mathrm{2}} +{c}^{\mathrm{2}} }} \\ $$$$\mathrm{tan}\:\varphi=\frac{{b}\:\mathrm{cos}\:\phi}{{a}\:\mathrm{sin}\:\phi} \\ $$$$\Rightarrow\mathrm{sin}\:\varphi=\frac{{b}\:\mathrm{cos}\:\phi}{\:\sqrt{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\phi+{b}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\phi}} \\ $$$$\Rightarrow\mathrm{cos}\:\varphi=\frac{{a}\:\mathrm{sin}\:\phi}{\:\sqrt{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\phi+{b}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\phi}} \\ $$$${x}_{{S}} ={p}+{r}\:\mathrm{sin}\:\theta={p}+\frac{\mathrm{2}{pr}}{\:\sqrt{\mathrm{4}{p}^{\mathrm{2}} +{c}^{\mathrm{2}} }} \\ $$$${y}_{{S}} =\frac{{p}^{\mathrm{2}} }{{c}}+{b}+{r}\:\mathrm{cos}\:\theta=\frac{{p}^{\mathrm{2}} }{{c}}+{b}+\frac{{cr}}{\:\sqrt{\mathrm{4}{p}^{\mathrm{2}} +{c}^{\mathrm{2}} }}={r} \\ $$$$\Rightarrow\frac{{p}^{\mathrm{2}} }{{c}}+{b}+\frac{{cr}}{\:\sqrt{\mathrm{4}{p}^{\mathrm{2}} +{c}^{\mathrm{2}} }}={r} \\ $$$$\Rightarrow\mathrm{4}{p}^{\mathrm{2}} +{c}^{\mathrm{2}} +\frac{\mathrm{4}{cr}}{\:\sqrt{\mathrm{4}{p}^{\mathrm{2}} +{c}^{\mathrm{2}} }}=\mathrm{4}{cr}+{c}^{\mathrm{2}} −\mathrm{4}{bc} \\ $$$${let}\:{u}=\sqrt{\mathrm{4}{p}^{\mathrm{2}} +{c}^{\mathrm{2}} } \\ $$$$\Rightarrow{u}^{\mathrm{3}} −\left(\mathrm{4}{cr}+{c}^{\mathrm{2}} −\mathrm{4}{bc}\right){u}+\mathrm{4}{cr}=\mathrm{0} \\ $$$$\Rightarrow{u}=…… \\ $$$$\Rightarrow{p}=\frac{\sqrt{{u}^{\mathrm{2}} −{c}^{\mathrm{2}} }}{\mathrm{2}}=……{in}\:{terms}\:{of}\:{r}\:\:\:…\left({i}\right) \\ $$$${x}_{{S}} ={a}\:\mathrm{cos}\:\phi+{r}\:\mathrm{sin}\:\varphi=\mathrm{cos}\:\phi\left({a}+\frac{{br}}{\:\sqrt{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\phi+{b}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\phi}}\right) \\ $$$${y}_{{S}} ={b}\:\mathrm{sin}\:\phi+{r}\:\mathrm{cos}\:\varphi=\mathrm{sin}\:\phi\left({b}+\frac{{ar}}{\:\sqrt{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\phi+{b}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\phi}}\right)={r} \\ $$$$ \\ $$$$\Rightarrow\frac{{br}}{\:\sqrt{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\mathrm{sin}^{\mathrm{2}} \:\phi+{b}^{\mathrm{2}} }}=\frac{{b}\left({r}−{b}\:\mathrm{sin}\:\phi\right)}{{a}\:\mathrm{sin}\:\phi} \\ $$$$\mathrm{cos}\:\phi\left({a}+\frac{{br}}{\:\sqrt{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\phi+{b}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\phi}}\right)={p}+\frac{\mathrm{2}{pr}}{\:\sqrt{\mathrm{4}{p}^{\mathrm{2}} +{c}^{\mathrm{2}} }} \\ $$$$\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\:\mathrm{sin}^{\mathrm{2}} \:\phi+{br}}{{a}\:\mathrm{tan}\:\phi}={p}+\frac{\mathrm{2}{pr}}{\:\sqrt{\mathrm{4}{p}^{\mathrm{2}} +{c}^{\mathrm{2}} }} \\ $$$$\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\frac{\mathrm{tan}^{\mathrm{2}} \:\phi}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\phi}+{br}=\left({p}+\frac{\mathrm{2}{pr}}{\:\sqrt{\mathrm{4}{p}^{\mathrm{2}} +{c}^{\mathrm{2}} }}\right)\mathrm{tan}\:\phi \\ $$$${let}\:{v}=\mathrm{tan}\:\phi \\ $$$$\Rightarrow\left({p}+\frac{\mathrm{2}{pr}}{\:\sqrt{\mathrm{4}{p}^{\mathrm{2}} +{c}^{\mathrm{2}} }}\right){v}^{\mathrm{3}} −\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{br}\right){v}^{\mathrm{2}} +\left({p}+\frac{\mathrm{2}{pr}}{\:\sqrt{\mathrm{4}{p}^{\mathrm{2}} +{c}^{\mathrm{2}} }}\right){v}−{br}=\mathrm{0} \\ $$$$\Rightarrow{v}=…… \\ $$$$\Rightarrow\phi=\mathrm{tan}^{−\mathrm{1}} {v}=……\:{in}\:{terms}\:{of}\:{p},\:{r}\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$$\mathrm{sin}\:\phi\left({b}+\frac{{ar}}{\:\sqrt{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\phi+{b}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\phi}}\right)={r} \\ $$$$\Rightarrow\frac{{ar}}{\:\sqrt{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\mathrm{sin}^{\mathrm{2}} \:\phi+{b}^{\mathrm{2}} }}=\frac{{r}−{b}\:\mathrm{sin}\:\phi}{\mathrm{sin}\:\phi} \\ $$$$\Rightarrow\frac{{a}^{\mathrm{2}} {r}^{\mathrm{2}} }{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\mathrm{sin}^{\mathrm{2}} \:\phi+{b}^{\mathrm{2}} }=\frac{{r}^{\mathrm{2}} −\mathrm{2}{br}\:\mathrm{sin}\:\phi+{b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\phi}{\mathrm{sin}^{\mathrm{2}} \:\phi} \\ $$$$\left[{r}^{\mathrm{2}} −\mathrm{2}{br}\:\mathrm{sin}\:\phi+{b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\phi\right]\left[\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\mathrm{sin}^{\mathrm{2}} \:\phi+{b}^{\mathrm{2}} \right]={a}^{\mathrm{2}} {r}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\phi \\ $$$$\Rightarrow\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){b}\:\mathrm{sin}^{\mathrm{4}} \:\phi−\mathrm{2}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){r}\:\mathrm{sin}^{\mathrm{3}} \:\phi−{b}\left({r}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\mathrm{sin}^{\mathrm{2}} \:\phi−\mathrm{2}{b}^{\mathrm{2}} {r}\:\mathrm{sin}\:\phi+{br}^{\mathrm{2}} =\mathrm{0}\:\:\:…\left({iii}\right) \\ $$$$ \\ $$$${with}\:\left({i}\right)\:{and}\:\left({ii}\right)\:{in}\:\left({iii}\right)\:{we}\:{can}\:{get}\:{r}. \\ $$$$….. \\ $$
Commented by ajfour last updated on 10/Apr/20
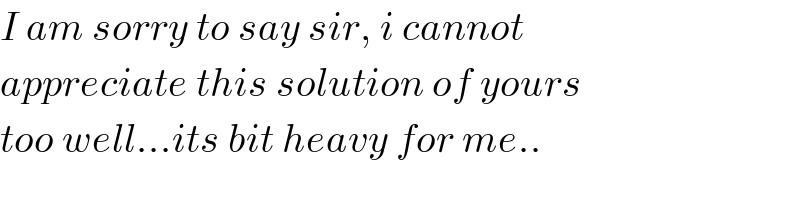
$${I}\:{am}\:{sorry}\:{to}\:{say}\:{sir},\:{i}\:{cannot} \\ $$$${appreciate}\:{this}\:{solution}\:{of}\:{yours} \\ $$$${too}\:{well}…{its}\:{bit}\:{heavy}\:{for}\:{me}.. \\ $$
Commented by mr W last updated on 10/Apr/20

$${i}\:{am}\:{also}\:{not}\:{satisfied}\:{with}\:{this} \\ $$$${solution},\:{but}\:{i}\:{found}\:{only}\:{this}\:{way}\:{to} \\ $$$${get}\:{a}\:{single}\:{final}\:{equation}\:{for}\:{the} \\ $$$${unknown}\:{r}. \\ $$
Commented by ajfour last updated on 10/Apr/20

$${Nevertheless}\:{great}\:{effort}\:{sir}, \\ $$$${thanks}\:{for}\:{attempting}; \\ $$$${Did}\:{you}\:{view}\:{my}\:{answer}\:{post} \\ $$$${to}\:{this}\:{question}? \\ $$
