Question-88388

Question Number 88388 by M±th+et£s last updated on 10/Apr/20

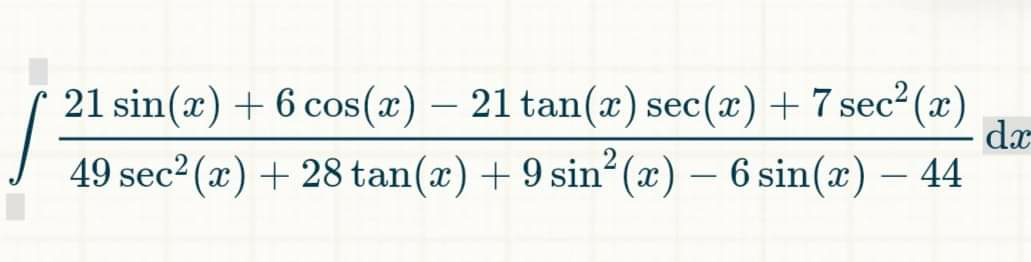
Answered by mind is power last updated on 10/Apr/20

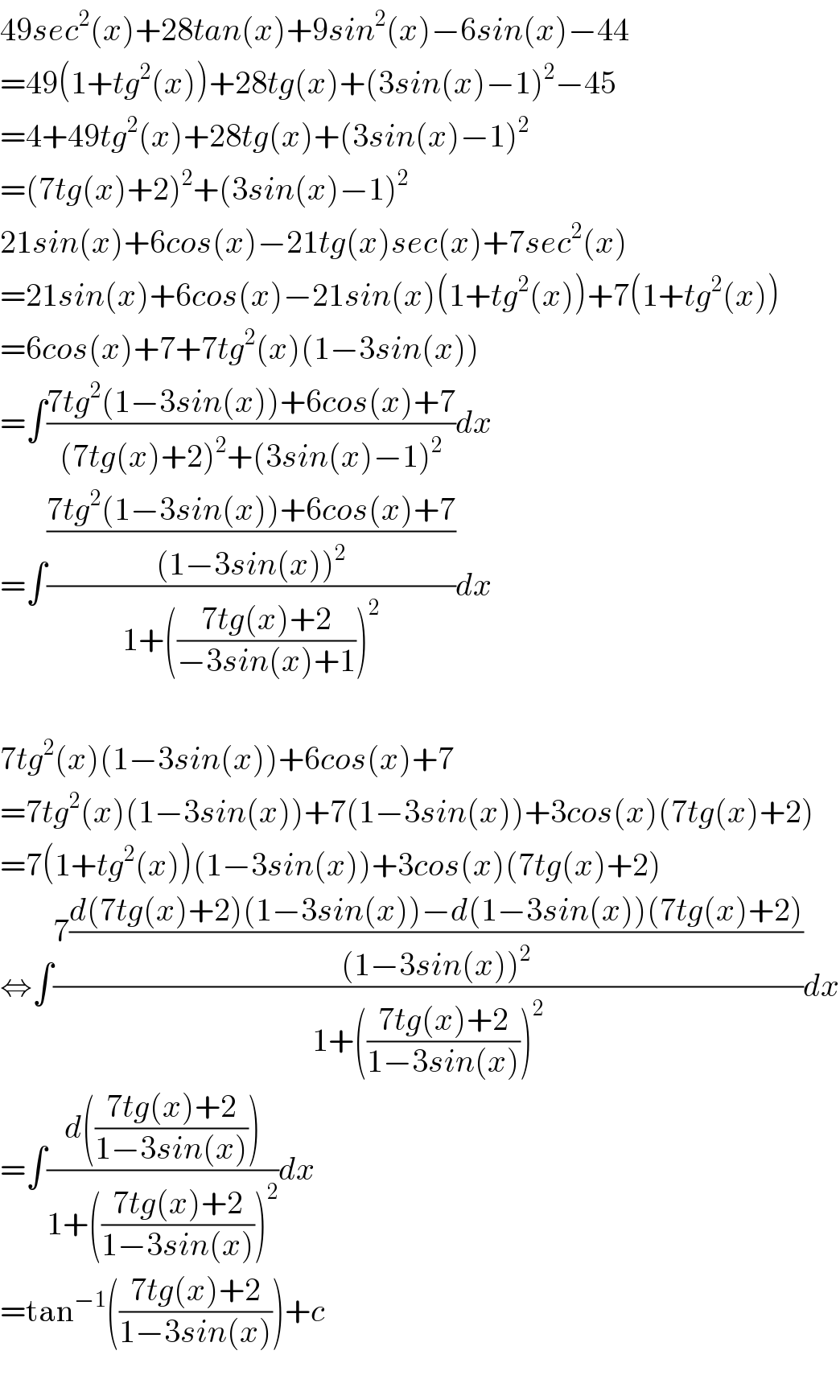
49sec^2 (x)+28tan(x)+9sin^2 (x)−6sin(x)−44 =49(1+tg^2 (x))+28tg(x)+(3sin(x)−1)^2 −45 =4+49tg^2 (x)+28tg(x)+(3sin(x)−1)^2 =(7tg(x)+2)^2 +(3sin(x)−1)^2 21sin(x)+6cos(x)−21tg(x)sec(x)+7sec^2 (x) =21sin(x)+6cos(x)−21sin(x)(1+tg^2 (x))+7(1+tg^2 (x)) =6cos(x)+7+7tg^2 (x)(1−3sin(x)) =∫((7tg^2 (1−3sin(x))+6cos(x)+7)/((7tg(x)+2)^2 +(3sin(x)−1)^2 ))dx =∫(((7tg^2 (1−3sin(x))+6cos(x)+7)/((1−3sin(x))^2 ))/(1+(((7tg(x)+2)/(−3sin(x)+1)))^2 ))dx 7tg^2 (x)(1−3sin(x))+6cos(x)+7 =7tg^2 (x)(1−3sin(x))+7(1−3sin(x))+3cos(x)(7tg(x)+2) =7(1+tg^2 (x))(1−3sin(x))+3cos(x)(7tg(x)+2) ⇔∫((7((d(7tg(x)+2)(1−3sin(x))−d(1−3sin(x))(7tg(x)+2))/((1−3sin(x))^2 )))/(1+(((7tg(x)+2)/(1−3sin(x))))^2 ))dx =∫((d(((7tg(x)+2)/(1−3sin(x)))))/(1+(((7tg(x)+2)/(1−3sin(x))))^2 ))dx =tan^(−1) (((7tg(x)+2)/(1−3sin(x))))+c

$$\mathrm{49}{sec}^{\mathrm{2}} \left({x}\right)+\mathrm{28}{tan}\left({x}\right)+\mathrm{9}{sin}^{\mathrm{2}} \left({x}\right)−\mathrm{6}{sin}\left({x}\right)−\mathrm{44} \\ $$$$=\mathrm{49}\left(\mathrm{1}+{tg}^{\mathrm{2}} \left({x}\right)\right)+\mathrm{28}{tg}\left({x}\right)+\left(\mathrm{3}{sin}\left({x}\right)−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{45} \\ $$$$=\mathrm{4}+\mathrm{49}{tg}^{\mathrm{2}} \left({x}\right)+\mathrm{28}{tg}\left({x}\right)+\left(\mathrm{3}{sin}\left({x}\right)−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$=\left(\mathrm{7}{tg}\left({x}\right)+\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{3}{sin}\left({x}\right)−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{21}{sin}\left({x}\right)+\mathrm{6}{cos}\left({x}\right)−\mathrm{21}{tg}\left({x}\right){sec}\left({x}\right)+\mathrm{7}{sec}^{\mathrm{2}} \left({x}\right) \\ $$$$=\mathrm{21}{sin}\left({x}\right)+\mathrm{6}{cos}\left({x}\right)−\mathrm{21}{sin}\left({x}\right)\left(\mathrm{1}+{tg}^{\mathrm{2}} \left({x}\right)\right)+\mathrm{7}\left(\mathrm{1}+{tg}^{\mathrm{2}} \left({x}\right)\right) \\ $$$$=\mathrm{6}{cos}\left({x}\right)+\mathrm{7}+\mathrm{7}{tg}^{\mathrm{2}} \left({x}\right)\left(\mathrm{1}−\mathrm{3}{sin}\left({x}\right)\right) \\ $$$$=\int\frac{\mathrm{7}{tg}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{3}{sin}\left({x}\right)\right)+\mathrm{6}{cos}\left({x}\right)+\mathrm{7}}{\left(\mathrm{7}{tg}\left({x}\right)+\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{3}{sin}\left({x}\right)−\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$=\int\frac{\frac{\mathrm{7}{tg}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{3}{sin}\left({x}\right)\right)+\mathrm{6}{cos}\left({x}\right)+\mathrm{7}}{\left(\mathrm{1}−\mathrm{3}{sin}\left({x}\right)\right)^{\mathrm{2}} }}{\mathrm{1}+\left(\frac{\mathrm{7}{tg}\left({x}\right)+\mathrm{2}}{−\mathrm{3}{sin}\left({x}\right)+\mathrm{1}}\right)^{\mathrm{2}} }{dx} \\ $$$$ \\ $$$$\mathrm{7}{tg}^{\mathrm{2}} \left({x}\right)\left(\mathrm{1}−\mathrm{3}{sin}\left({x}\right)\right)+\mathrm{6}{cos}\left({x}\right)+\mathrm{7} \\ $$$$=\mathrm{7}{tg}^{\mathrm{2}} \left({x}\right)\left(\mathrm{1}−\mathrm{3}{sin}\left({x}\right)\right)+\mathrm{7}\left(\mathrm{1}−\mathrm{3}{sin}\left({x}\right)\right)+\mathrm{3}{cos}\left({x}\right)\left(\mathrm{7}{tg}\left({x}\right)+\mathrm{2}\right) \\ $$$$=\mathrm{7}\left(\mathrm{1}+{tg}^{\mathrm{2}} \left({x}\right)\right)\left(\mathrm{1}−\mathrm{3}{sin}\left({x}\right)\right)+\mathrm{3}{cos}\left({x}\right)\left(\mathrm{7}{tg}\left({x}\right)+\mathrm{2}\right) \\ $$$$\Leftrightarrow\int\frac{\mathrm{7}\frac{{d}\left(\mathrm{7}{tg}\left({x}\right)+\mathrm{2}\right)\left(\mathrm{1}−\mathrm{3}{sin}\left({x}\right)\right)−{d}\left(\mathrm{1}−\mathrm{3}{sin}\left({x}\right)\right)\left(\mathrm{7}{tg}\left({x}\right)+\mathrm{2}\right)}{\left(\mathrm{1}−\mathrm{3}{sin}\left({x}\right)\right)^{\mathrm{2}} }}{\mathrm{1}+\left(\frac{\mathrm{7}{tg}\left({x}\right)+\mathrm{2}}{\mathrm{1}−\mathrm{3}{sin}\left({x}\right)}\right)^{\mathrm{2}} }{dx} \\ $$$$=\int\frac{{d}\left(\frac{\mathrm{7}{tg}\left({x}\right)+\mathrm{2}}{\mathrm{1}−\mathrm{3}{sin}\left({x}\right)}\right)}{\mathrm{1}+\left(\frac{\mathrm{7}{tg}\left({x}\right)+\mathrm{2}}{\mathrm{1}−\mathrm{3}{sin}\left({x}\right)}\right)^{\mathrm{2}} }{dx} \\ $$$$=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{7}{tg}\left({x}\right)+\mathrm{2}}{\mathrm{1}−\mathrm{3}{sin}\left({x}\right)}\right)+{c} \\ $$$$ \\ $$

Commented by john santu last updated on 10/Apr/20

$${amazing}\:{sir} \\ $$

Commented by M±th+et£s last updated on 10/Apr/20

$${great}\:{solution} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply